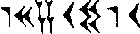
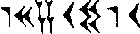
has been found on an old Babylonian tablet from the Yale collection. It is an approximation for the square root of two. The symbols are 1, 24, 51, and 10. Because the Babylonians used a base 60, or sexagesimal, system, this number is 1 x 600 + 24 x 60-1 + 51 x 60-2 + 10 x 60-3, or about 1.414222.
The Babylonian system of numeration was not a pure positional system because of the absence of a symbol for zero. In the older tablets, a space was placed in the appropriate place in the numeral; in some later tablets, a symbol for zero does appear but in the tablets which have been discovered, this symbol only used between other symbols and never in a terminal position.
The earliest Egyptian and Greek fractions were usually unit fractions (having a numerator of 1), so that the fraction was shown simply by writing a numeral with a mark above or to the right indicating that the numeral was the denominator of a fraction.
Ancient Rome. The Romans did not use numerals to indicate fractions, but instead used words to indicate parts of a whole. A unit of weight was the as and the uncia (from which we have the word "ounce") was a twelfth part of the as. The following words were used to indicate parts of the as or, more generally, parts of any quantity:
| 11/12 | deunx | for de uncia, 1/12 taken away |
| 10/12 | dextans | for de sextans, 1/6 taken away |
| 9/12 | dodrans | for de quadrans, 1/4 taken away |
| 8/12 | bes | bi as for duae partes, 2/3 |
| 7/12 | septunx | for septem unciae |
| 6/12 | semis | |
| 5/12 | quincunx | for quinque unciae |
| 4/12 | triens | |
| 3/12 | quadrans | |
| 2/12 | sextans | |
| 1/12 | uncia | |
| 1/24 | semuncia | |
| 1/48 | sicilicus | |
| 1/72 | scriptulum | |
| 1/144 | scripulum | |
| 1/288 | scrupulum |
Multiples of the as were indicated using the following scheme, in which a denarius represents 16 asses. Denarii semuncia sicilicus represented 1/24 + 1/48 of a denarius or 1/16 denarius, or 1 as. Denarii uncia semuncia represented 1/12 + 1/24 of a denarius or 1/8 denarius, or 2 asses. Denarii sextans sicilicus represented 1/6 + 1/48 of a denarius, or 3/16 denarius, or 3 asses. Denarii deunx sicilicus represented 11/12 + 1/48 of a denarius, or 15/16 denarius, or 15 asses [Smith vol. 2, pages 208-209].
Ordinary fractions without the horizontal bar. According to Smith (vol. 2, page 215), it is probable that our method of writing common fractions is due essentially to the Hindus, although they did not use the bar. Brahmagupta (c. 628) and Bhaskara (c. 1150) wrote fractions as we do today but without the bar.
The horizontal fraction bar was introduced by the Arabs. "The Arabs at first copied the Hindu notation, but later improved on it by inserting a horizontal bar between the two numbers" (Burton).
Several sources attribute the horizontal fraction bar to al-Hassar around 1200.
When Rabbi ben Ezra (c. 1140) adopted the Moorish forms he generally omitted the bar.
Fibonacci (c.1175-1250) was the first European mathematician to use the fraction bar as it is used today. He followed the Arab practice of placing the fraction to the left of the integer (Cajori vol. 1, page 311).
According to the DSB, Abu Abdallah Yaish ibn Ibrahim ibn Yusuf ibn Simak al-Umawi (14th or 15th century) insisted that the horizontal fraction bar be used, whereas easterners continued to write it without the bar.
The bar is generally found in Latin manuscripts of the late Middle Ages, but when printing was introduced it was frequently omitted, doubtless owing to typographical difficulties. This inference is confirmed by such books as Rudolff's Kunstliche rechnung (1526), where the bar is omitted in all ordinary fractions but is inserted in fractions printed in larger type and those having large numbers (Smith vol. 2, page 216).
Michael Closs points out that if we define a horizontal fraction bar to be a horizontal line that separates the numerator from the denominator and demarcates them as such, then this type of notation was used with exactly that purpose more than a millennium before al-Hassar. In Demotic Mathematical Papyri, (Brown University Press, London, 1972, pages 8-9) Richard A. Parker writes that in three papyri dating from the third century B. C. to the Roman period, "the numerator is written first, and the denominator follows on the same line. In problems 2, 3, 10, and 13 (the Cairo papyrus) the numerator is underlined. In problems 51 and 72 the denominator is underlined."
Some writers use the term vinculum for the horizontal fraction bar. This term originally applied to the mark when used as a grouping symbol. Fibonacci used the Latin word virga for the horizontal fraction bar.
The diagonal fraction bar (also called a solidus or virgule) was introduced because the horizontal fraction bar was difficult typographically, requiring three terraces of type.
An early handwritten document with forward slashes in lieu of fraction bars is Thomas Twining's Ledger of 1718, where quantities of tea and coffee transactions are listed, e.g. 1/4 pound green tea. This usage of the horizontal fraction bar was found by Hans Lausch, who believes there are likely even earlier occurrences.
Lausch has also found the horizontal fraction bar in Allgemeine Deutsche Bibliothek, a Berlin review journal which was started in 1765. A precise reference may be forthcoming.
The earliest instance of a diagonal fraction bar shown by Cajori (vol. 1, page 313) is in 1784, when a curved line resembling the sign of integration was used in the Gazetas de Mexico by Manuel Antonio Valdes.
In 1843, a curved line was used by Henri Cambuston in Definicion de las principales operaciones de arismetica (Cajori vol. 1, page 313)
In 1845, the use of the solidus was recommended by De Morgan in an article "The Calculus of Functions" published in the Encyclopaedia Metropolitana of 1845 (Cajori vol. 1, page 313).
In 1852, the solidus was used by Antonio Serra Y Oliveres in Manuel de la Tipografia Española (Cajori vol. 1, page 313).
Decimal fractions. Abu'l Hasan Ahmad ibn Ibrahim Al-Uqlidisi (c. 920-c. 980) wrote the earliest known text offering a direct treatment of decimal fractions. "Al-Uqlidisi uses decimal fractions as such, appreciates the importance of a decimal sign, and suggests a good one," according to A. S. Saidan, "The earliest extant Arabic arithmetic," Isis 57 (1966), 475-490.
The idea of decimal fractions had been present in the work of several mathematicians of al-Karaji's school, in particular Ibn Yahya al-Maghribi Al-Samawal (c. 1130-c. 1180), according to the University of St. Andrews website.
In The Key to Arithmetic, Ghiyath al-Din Jamshid Mas'ud al-Kashi (c. 1380-1429) gave a clear description of decimal fractions, according to P. Luckey, Die Rechnenkunst bei Gamsid b. Masud al-Kasi (1951).
Al-Kashi in his al-Risali al-mohitije (Treatise on the
circumference) wrote the value of pi using Arabic characters as
follows:
sah-hah
3 1415926535898732
The word sah-hah meant complete, correct, integral. (The
modern Turkish form is sahih.) Thus the part at the right is
the decimal, although there is no decimal point. According to Smith
(vol. 2, page 240), "Manifestly it is, therefore, a clear case of a
decimal fraction, and it seems to be earlier than any similar one to
be found in Europe."
Yang Hui (c. 1238-c. 1298) was a minor Chinese official who wrote two books, dated 1261 and 1275, which use decimal fractions (in the modern form). The 1275 work is called Cheng Chu Tong Bian Ben Mo [University of St. Andrews website].
Smith (vol. 1, page 255) writes, "Francesco Pellos or Pellizzati, a native of Nice, published a commercial arithmetic at Turin in 1492 in which, as will be shown in Volume II, use is made of a decimal point to denote the division of a number by a power of ten." In vol. 2 (page 138) Smith says Pellos "unwittingly made use of the decimal point for the first time in a printed work" and that he "did not recognize the significance of the decimal point." Cajori (vol. 1, page 315) says Pellos "used a point and came near the invention of decimal fractions."
In 1530, Christoff Rudolff (1499?-1545?) used a vertical bar exactly as we use a decimal point today in setting up a compound interest table in the Exempel Büchlin (Cajori vol. 1, page 316).
Smith (vol. 2, page 240) writes:
The first man who gave evidence of having fully comprehended the significance of all this preliminary work seems to have been Christoff Rudolff, whose Exempel Büchlin appeared at Augsburg in 1530. In this work he solved an example in compound interest, and used the bar precisely as we should use a decimal point today. If any particular individual were to be named as having the best reason to be called the inventor of decimal fractions, Rudolff would seem to be the man, because he apparently knew how to operate with these forms as well as merely to write them, as various predecessors had done. His work, however, was not appreciated, and apparently was not understood, and it was not until 1585 that a book upon the subject appeared.
In 1579 Francois Vieta (1540-1603) published a work which included a systematic use of decimal fractions, using a vertical stroke as a separator; "from the vertical stroke to the actual comma there is no great change" (Cajori vol. 1, page 316).
In 1585 Simon Stevin (or Stevinus) (1548-1620) published La
Thiende ("The Tenth") and La Disme ("The Decimal"), both
of which explained the use of decimal fractions. He is credited with
introducing decimal fractions into common use, although he did not
use the notation we use today. He wrote 5.912 as 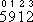 or
or 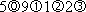 .
.
Boyer writes (on page 340):
The use of a decimal point separatrix generally is attributed either to G. A. Magini (1555-1617), a map-making friend of Kepler and rival of Galileo for a chair at Bologna, in his De planis triangulis of 1592, or to Christoph Clavius (1537-1612), a Jesuit friend of Kepler, in a table of sines of 1593. But the decimal point did not become popular until Napier used it more than twenty years later.Jobst Bürgi (1552-1632) "was not clear as to the best method of representing these fractions, however, and in his manuscript of 1592 he used both a period and a comma for the decimal point" (Smith vol. 2, page 243-244). He also used instead a small circle placed above or below the units digit (Smith vol. 2, page 244 and Cajori (vol. 1, page 317).
In 1593 Christopher Clavius (1537-1612) used a period to separate the units and tenths digits in a table of sines in Astrolabe. However, he used the period for other reasons in his works, and his purpose in using the period in this case is not clear (Cajori vol. 1, page 322). Carl Boyer says Clavius was the first person to use the decimal point with a clear idea of its significance.
William Oughtred (1574-1660) did not use a decimal point, but instead wrote 0.56 as 0/56, with the 56 underlined.
The dot as a separator occurs in 1616 in E. Wright's translation of John Napier's Descriptio. Boyer refers to this as the first appearance of a decimal point separating the whole number part from the decimal part, in the notation we use today. However Cajori (vol. 1, page 323) says "no evidence has been advanced, thus far, to show that the sign was intended as a separator of units and tenths, and not as a more general separator as in Pitiscus." According to Scott (p. 128), "Wright's translation of his treatise on logarithms, which was published in 1616 shows the decimal point on the first page."
In 1617 in his Latin Rabdologia, Napier used both the comma and the period as separators of units and tenths. Before 1617, he used the period in his Constructio, which was not published until 1619 (Cajori vol. 1, page 324).
The percent symbol is believed to have evolved from a symbol introduced in an anonymous Italian manuscript of about 1425, according to D. E. Smith in Rara arithmetica in 1898.