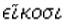 twenty +
twenty + 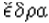 seat, base.
The English word is found in Sir Henry Billingsley’s 1570 translation of the Elements (OED).
seat, base.
The English word is found in Sir Henry Billingsley’s 1570 translation of the Elements (OED).Last revision: Aug. 27, 2018
ICOSAHEDRON. The icosahedron is treated in
Euclid’s Elements XIII. xvi.
The word is formed from 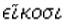 twenty +
twenty + 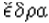 seat, base.
The English word is found in Sir Henry Billingsley’s 1570 translation of the Elements (OED).
seat, base.
The English word is found in Sir Henry Billingsley’s 1570 translation of the Elements (OED).
IDEAL (point or line) was introduced as idéal by J. V. Poncelet in Traité des Propriétés proj. des Figures (1822).
IDEAL (number theory) was introduced by Richard Dedekind (1831-1916) in his edition of P. G. L. Dirichlet Vorlesungen über Zahlentheorie (ed. 2, 1871) Suppl. x. p. 452. According to Kline (p. 823), the name was chosen “in honor of Kummer’s ideal numbers.” See also the article in the Encyclopaedia of Mathematics.
The term passed without change into English. A JSTOR search produced references to Dedekind’s theory of ideals in Arthur S. Hathaway “A Memoir in the Theory of Numbers,” American Journal of Mathematics, 9, (Jan., 1887), p. 166: “The theory of ideals here established, however, differs from Dedekind’s theory in important respects…” [John Aldrich]
See the entry IDEAL NUMBER.
IDEAL NUMBER. According to Kline (p. 819), Ernst Eduard Kummer (1810-1893) created a theory of ideal numbers in the papers he published in the Journal für die reine und angewandte Mathematik, 12, 1847: “Zur Theorie der complexen Zahlen” (pp. 319-326) and “Ueber die Zerlegung der aus Wurzeln der Einheit gebildeten complexen Zahlen in ihre Primfactoren” (pp. 327-367). See also the article in the Encyclopaedia of Mathematics.
The English term is found in H. J. S. Smith’s “Report on the Theory of Numbers.—Part II” Report Of The Thirty-First Meeting Of The British Association For The Advancement Of Science; Held At Manchester In September 1861. (The text is available through Google books.) [John Aldrich]
IDEMPOTENT and NILPOTENT were used by Benjamin Peirce (1809-1880) in 1870:
When an expression raised to the square or any higher power vanishes, it may be called nilpotent; but when, raised to a square or higher power, it gives itself as the result, it may be called idempotent.
The defining equation of nilpotent and idempotent expressions are respectively An = 0, and An = A; but with reference to idempotent expressions, it will always be assumed that they are of the form
unless it be otherwise distinctly stated.This citation is excerpted from "Linear Associative Algebra," a memoir read by Benjamin Peirce before the National Academy of Sciences in Washington, 1870, and published by him as a lithograph in 1870. In 1881, Peirce’s son, Charles S. Peirce, reprinted it in the American Journal of Mathematics. [Julio González Cabillón]
The OED2 shows a 1937 citation with a simplified definition of idempotent in Modern Higher Algebra (1938) iii 88 by A. A. Albert: "A matrix E is called idempotent if E2 = E. [Older dictionaries pronounce idempotent with the only stress on the second syllable, but newer ones show a primary stress on the first syllable and a secondary stress on the penult.]
The term IDENTIFIABILITY was coined by the econometrician Tjalling C. Koopmans around 1945 with reference to the economic identity of a relationship within a system of relationships. (See SIMULTANEOUS EQUATIONS MODEL). The term began appearing in the econometrics literature immediately, although Koopmans’s own exposition of the subject did not appear until 1949--his "Identification Problems in Economic Model Construction" Econometrica, 17, pp. 125-144. Around 1950 the term was taken up by statistical theorists and used in a more general sense, see e.g. Jerzy Neyman’s "Existence of Consistent Estimates of the Directional Parameter in a Linear Structural Relation Between Two Variables," Annals of Mathematical Statistics, 22, (1951), pp. 497-512. [John Aldrich]
IDENTITY (type of equation) is found in 1831 in the second edition of Elements of the Differential Calculus (1836) by John Radford Young: "This is obvious, for this first term is what the whole development reduces to when h = 0, but we must in this case have the identity f(x) = f(x); hence f(x) is the first term" [James A. Landau].
Young also uses the term identical equations in the same work.
IDENTITY and IDENTITY-ELEMENT are found in 1894 in “The Group of Holoedric Transformation Into Itself of a Given Group” by Prof. E. Hastings Moore in Bulletin of the American Mathematical Society. [OED and Google print search by James A. Landau]
IDENTITY MATRIX is found in "Representations of the General Symmetric Group as Linear Groups in Finite and Infinite Fields," Leonard Eugene Dickson, Transactions of the American Mathematical Society, Vol. 9, No. 2. (Apr., 1908).
The term is also found in "Concerning Linear Substitutions of Finite Period with Rational Coefficients," Arthur Ranum, Transactions of the American Mathematical Society, Vol. 9, No. 2. (Apr., 1908).
An earlier term was unit-matrix; see e.g. J. J. Sylvester "Note on the Theory of Simultaneous Linear Differential of Difference Equations with Constant Coefficients," American Journal of Mathematics, 4, (1881), 321-326, Coll Math Papers, III, pp. 551-6. The matrix unity was the term used by A. Cayley "A Memoir on the Theory of Matrices" (1858) Coll Math Papers, II, p. 477.
IFF. The earliest citation for “iff” in the OED is from John L. Kelley’s General Topology (1955): “F is equicontinuous at x iff there is a neighborhood of x whose image under every member of F is small.” Kelley credited the term to Paul R. Halmos.
On the last page of his autobiography, Halmos writes:
My most nearly immortal contributions are an abbreviation and a typographical symbol. I invented “iff”, for “if and only if”—but I could never believe that I was really its first inventor. I am quite prepared to believe that it existed before me, but I don't know that it did, and my invention (re-invention?) of it is what spread it through the mathematical world. The symbol is definitely not my invention—it appeared in popular magazines (not mathematical ones) before I adopted it, but, once again, I seem to have introduced it into mathematics. It is the symbol that sometimes looks like▐, and is used to indicate an end, usually the end of a proof. It is most frequently called the “tombstone”, but at least one generous author referred to it as the “halmos”.
From I Want to Be a Mathematician: An Automathography, by Paul R. Halmos, Springer-Verlag, New York, Berlin, Heidelberg, Tokyo, 1985, page 403. See Wolfram: iff.
For the halmos, see Earliest Uses of Symbols of Set Theory and Logic.
The terms IMAGINARY and REAL were introduced in French by Rene Descartes (1596-1650) in "La Geometrie" (1637):
...tant les vrayes racines que les fausses ne sont pas tousiours réelles; mais quelquefois seulement imaginaires; c'est à dire qu'on peut bien toujiours en imaginer autant que aiy dit en chàsque Equation; mais qu'il n'y a quelquefois aucune quantité, qui corresponde à celles qu'on imagine. comme encore qu'on en puisse imaginer trois en celle cy, x3 - 6xx + 13x - 10 = 0, il n'y en a toutefois qu'une réelle, qui est 2, & pour les deux autres, quois qu'on les augmente, ou diminué, ou multiplié en la façon que ie viens d'éxpliquer, on ne sçauroit les rendre autres qu'imaginaires. [...neither the true roots nor the false are always real; sometimes they are, however, imaginary; namely, whereas we can always imagine as many roots for each equation as I have predicted, there is still not always a quantity which corresponds to each root so imagined. Thus, while we may think of the equation x3 - 6xx + 13x - 10 = 0 as having three roots, yet there is just one real root, which is 2, and the other two, however, increased, diminished, or multiplied them as we just laid down, remain always imaginary.] (page 380)
Imaginary and real are found in English in 1668 in Philosophical Transactions. The words are found in a review of the book Geometriæ Universalis: “And for the like reason a Cubick Æquation, having three reals roots, can never be reduced to a pure Æquation, which hath but one onely root, for in these Æquations, Reduction shall no wise profit, forasmuch as ‘tis impossible, by aid thereof to change an Imaginary root into a real one, and the Converse.” [Google print search by James A. Landau]
As a way of removing the stigma of the name, the American mathematician Arnold Dresden (1882-1954) suggested that imaginary numbers be called normal numbers, because the term "normal" is synonymous with perpendicular, and the y-axis is perpendicular to the x-axis (Kramer, p. 73). The suggestion appears in 1936 in his An Invitation to Mathematics.
Some other terms that have been used to refer to imaginary numbers include "sophistic" (Cardan), "nonsense" (Napier), "inexplicable" (Girard), "incomprehensible" (Huygens), and "impossible" (many authors).
The first edition of the Encyclopaedia Britannica (1768-1771) has: "Thus the square root of -a2 cannot be assigned, and is what we call an impossible or imaginary quantity."
There are two modern meanings of the term imaginary number. In Merriam-Webster’s Collegiate Dictionary, 10th ed., an imaginary number is a number of the form a + bi where b is not equal to 0. In Calculus and Analytic Geomtry (1992) by Stein and Barcellos, "a complex number that lies on the y axis is called imaginary."
The term IMAGINARY GEOMETRY was used by Lobachevsky, who in 1835 published a long article, "Voobrazhaemaya geometriya" (Imaginary Geometry).
The term IMAGINARY PART appears in 1748 in A Treatise of Algebra: In Three Parts by Colin Maclaurin. [Google print search by James A. Landau]
The term IMAGINARY UNIT was used (and apparently introduced) by by Sir William Rowan Hamilton in "On a new Species of Imaginary Quantities connected with a theory of Quaternions," Proceedings of the Royal Irish Academy, Nov. 13, 1843: "...the extended expression...which may be called an imaginary unit, because its modulus is = 1, and its square is negative unity."
IMPLICIT DEFINITION. In the literature of mathematics, this term was introduced by Joseph-Diaz Gergonne (1771-1859) in Essai sur la théorie des définitions, Annales de Mathématique Pure et Appliquée (1818) 1-35, p. 23. (The Annales begun to be published by Gergonne himself in 1810.) He also emphasized the contrast between this kind of definition and the other "ordinary" ones which, according to him, should be called "explicit definitions". According to his own example, given the words "triangle" and "quadrilateral" we can define (implicitly) the word "diagonal" (of a quadrilateral) in a satisfactory way just by means of a property that individualizes it (namely, that of dividing the quadrilateral in two equal triangles). Gergonne’s observations are now viewed by many as an anticipation of the "modern" idea of "definition by axioms" which was so fruitfully explored by Dedekind, Peano and Hilbert in the second half of the nineteenth century. In fact, still today the axioms of a theory are treated in many textbooks as "implicit definitions" of the primitive concepts involved. We can also view Gergonne’s ideas as anticipating, to a certain extent, the use of "contextual definitions" in Russell’s theory of descriptions (1905). [Carlos César de Araújo]
IMPLICIT DIFFERENTIATION is found in English in 1836 in The differential and integral calculus by Augustus De Morgan. [Google print search]
IMPLICIT FUNCTION is found in 1814 New Mathematical and Philosophical Dictionary: "Having given the methods ... of obtaining the derived functions, of functions of one or more quantities, whether those functions be explicit or implicit, ... we will now show how this theory may be applied" (OED2).
IMPROPER FRACTION was used in English in 1542 by Robert Recorde in The ground of artes, teachyng the worke and practise of arithmetike: "An Improper Fraction...that is to saye, a fraction in forme, which in dede is greater than a Unit."
IMPROPER INTEGRAL occurs in "Concerning Harnack’s Theory of Improper Definite Integrals" by Eliakim Hastings Moore, Trans. Amer. Math. Soc., July 1901. The term may be much older.
INCENTER, INCIRCLE. See the entry CIRCUMCENTER, CIRCUMCIRCLE, EXCENTER, EXCIRCLE, INCENTER, INCIRCLE, MIDCIRCLE.
INCLUDED ANGLE and INCLUDED SIDE are found in 1753 in The Elements of Algebra in a New and Easy Method: Second Edition, Corrected, by Nathaniel Hammond. [Google print search by James A. Landau]
INCOMMENSURABLE. Incommensurability is found in Latin in the 1350s in the title De commensurabilitate sive incommensurabilitate motuum celi (the commensurability or incommensurability of celestial motions) by Nicole Oresme.
The term INDEFINITE INTEGRAL is defined by Sylvestre-François Lacroix (1765-1843) in Traité du calcul différentiel et integral (Cajori 1919, page 272).
Indefinite integral appears in English in 1823 in Dictionary of the Mathematical and Physical Sciences, According to the Latest Improvements and Discoveries, Edited by James Mitchell. [Google print search by James A. Landau]
INDEPENDENT EVENT and DEPENDENT EVENT are found in 1738 in The Doctrine of Chances by De Moivre: "Two Events are independent, when they have no connexion one with the other, and that the happening of one neither forwards nor obstructs the happening of the other. Two events are dependent, when they are so connected together as that the Probability of either’s happening is alter'd by the happening of the other."
INDEPENDENT VARIABLE. See DEPENDENT VARIABLE.
The term INDETERMINATE FORM is used in French in 1840 in Moigno, abbé (François Napoléon Marie), (1804-1884): Leçons de calcul différentiel et de calcul intégral, rédigées d'après les méthodes et les ouvrages publiés ou inédits de M. A.-L. Cauchy, par M. l'abbé Moigno. [V. Frederick Rickey]
Indeterminate Forms is found in English as a chapter title in 1841 in An Elementary Treatise on Curves, Functions, and Forces by Benjamin Pierce. [Google print search by James A. Landau]
Forms such as 0/0 are called singular values and singular forms in in 1849 in An Introduction to the Differential and Integral Calculus, 2nd ed., by James Thomson.
In Primary Elements of Algebra for Common Schools and Academies (1866) by Joseph Ray, 0/0 is called "the symbol of indetermination."
INDEX. Schoner, writing his commentary on the work of Ramus, in 1586, used the word "index" where Stifel had used "exponent" (Smith vol. 2).
INDEX NUMBER became a standard term in economic statistics in the 1880s. The OED’s earliest quotation is from 1875 William Stanley Jevons Money and the Mechanism of Exchange chapter xxv p. 332: "In the annual Commercial History and Review of the Economist newspaper, there has, for many years, appeared a table containing the Total Index Number of prices, or the arithmetical sum of the numbers expressing the ratios of the prices of many commodities to the average prices of the same commodities in the years 1845-50." The table was the work of William Newmarch but Jevons had himself pioneered the method of index numbers in A Serious Fall in the Value of Gold Ascertained and its Social Effects Set Forth (1863). Anticipations of the technique have been found in the early 18th century, in the work of William Fleetwood. See M. G. Kendall "The Early History of Index Numbers" in M. G. Kendall & R. L. Plackett Studies in the History of Statistics and Probability, volume 2 (1977).
INDICATOR. See totient.
INDICATOR FUNCTION and INDICATOR RANDOM VARIABLE. The term indicator of a set appears in M. Loève’s Probability Theory (1955) and, according to W. Feller (An Introduction to Probability Theory and its Applications volume II), Loève was responsible for the term. Loève’s Probability Theory did not use term indicator random variable but this soon appeared, see e.g. H. D. Brunk’s "On an Extension of the Concept Conditional Expectation" Proceedings of the American Mathematical Society, 14, (1963), pp. 298-304.
See CHARACTERISTIC FUNCTION of a set and BERNOULLI DISTRIBUTION.
INDUCE. Adolf Hurwitz introduced the use of the verb induce in mathematics, as in the case in which a rotation of the octahedron induces a permutation of its vertices, according to the third edition of Die Theorie der Gruppen von endlicher Ordnung by Andreas Speiser. [Information provided by Robert Alan Wolf.]
The term INDUCTION was first used in the phrase per modum inductionis by John Wallis in 1656 in Arithmetica Infinitorum. Wallis was the first person to designate a name for this process; Maurolico and Pascal used no term for it (Burton, page 440). [See also mathematical induction, complete induction, successive induction. ]
INDUCTIVE (PARTIALLY) ORDERED SET. The adjective "inductive" used in this context was introduced by Bourbaki in Élements de mathématique. I. Théorie des ensembles. Fascicule de résultats, Actualités Scientifiques et Industrielles, no. 846, Hermann, Paris, 1939. Bourbaki’s original term and definition is now standard among mathematicians: a poset (X, £) is inductive if every totally ordered subset of it has a supremum, that is:
(1) ("A Ì X) (A is a chain Þ A has a supremum).
A notion of "completeness" is usually associated with conditions of this kind. Thus, if
(2) (" A Ì X) (A has a supremum),
then (X, £) becomes a "complete lattice." Similarly, (X, £) is said to be "order-complete" (or "Dedekind-complete") if
(3) (" A ÌX) (A Æ and A has an upper bound Þ A has a supremum).
This may explain why some computer scientists prefer the term "complete poset" instead of "inductive poset." (However, "complete poset" is also used by many of them in a related but different sense.)
[Carlos César de Araújo]
INFINITE DESCENT. Pierre de Fermat (1607?-1665) used the term method of infinite descent (Burton, page 488; DSB).
A paper by Fermat is titled "La méthode de la 'descente infinie ou indéfinie.'" Fermat stated that he named the method.
INFINITELY SMALL. A Google print search shows the Latin term infinite parva used by John Wallis in 1655 and 1656 [Mikhail Katz].
Infinitely small is found in English in 1685 in A Treatise of Algebra Both Historical and Practical by Jon Wallis.
According to the DSB, Christian Huygens used the term infinitely small.
INFINITESIMAL. In a letter from Wallis to the French mathematician Vincent Léotaud, dating from February 17/[27], 1667/[1668], a few months before the publication of Mercator’s Logarithmotechnia, Wallis proposes a change of terminology to Léotaud:
Dic Angulum Contactûs esse, Infinitesimam partem duorum Rectorum: (seu 2/∞ R.) [Say the angle of contact is an infinitesimal part [pars infinitesima] of two right angles (or 2/∞ R.)](See Philip Beeley / Christoph J. Scriba (eds.), Correspondence of John Wallis, vol. 2, p. 426). There seems to be no original manuscript of the letter extant, it has been printed for the first time by Wallis himself some years later in 1685 (A Defence of the Treatise of the Angle of Contact, p. 87).
Wallis used infinitesima in print in 1670:
Linea, ex infinitis punctis, hoc est, Lineolis infinite exiguis, longitudine aequalibus, vel aeque altis; quarum cujusvis longitudo vel altitudo sit 1/∞ (pars infinitesima) longitudinis vel altitudinis totius lineae
(Wallis, Mechanica, p. 110).
Leibniz seems to have started to use the term infinitesimal in late spring 1673 (see Gottfried Wilhelm Leibniz, Sämtliche Schriften und Briefe, Reihe VII: Mathematische Schriften, vol 4: Infinitesimalmathematik 1670-1673, Berlin : Akademie Verlag, 2008, pp. 263, 356, 398 etc.) on line.
Apparently Leibniz took the term from Nicholas Mercator’s writings, as he was to recall much later in a letter to John Wallis, March 30/[April 9], 1699 (Leibniz, Mathematische Schriften (ed. Gerhardt), vol. IV, p. 63). In his book Logarithmotechnia (1668) Mercator does not use the term infinitesimal, but instead pars infinitissima (pp. 30–34). But at the end of his article “Some illustration of the Logarithmotechnia,” Philosophical Transactions n° 38 (1668), pp. 759-764, Mercator added a note: “atque ubicunque, Lector offenderit infinitissimam, legat infinitesimam.” This was a reaction to the critique by Wallis at the beginning of his review of the book, printed in the same issue of the Philosophical Transactions, pp. 753-759.
[This information was contributed by Dr. Siegmund Probst.]
Infinitesimal is found in English with its modern meaning in 1706 in An Institution of Fluxions by Humphrey Ditton.
The word was used by Tolstoy in War and Peace: “Arriving at infinitesimals, mathematics, the most exact of sciences, abandons the process of analysis and enters on the new process of the integration of unknown, infinitely small, quantities.”
The term INFINITESIMAL ANALYSIS was used in 1748 by Leonhard Euler in Introductio in analysin infinitorum (Kline, page 324).
The term INFINITESIMAL CALCULUS is found in English in 1797 in the 3rd edition of the Encyclopaedia Britannica. [Google print search by James A. Landau]
INFIX NOTATION is found in 1962 in Algebraic Logic by Paul Halmos. [Google print search by James A. Landau]
INFLECTION POINT. In the last page of an appendix to his "Methodus ad disquirendam maximam & minimam," Fermat wrote:
Quia tamen sæpius curvatura mutatur, ut in conchoide Nicomedea, quæ pertinet ad priorem casum, et in omnibus speciebus curvæ Domini de Roberval (prima excepta) quæ pertinet ad secundum, ut perfecte curva possit delineari, investiganda sunt ex arte puncta inflexionum, in quibus curvatura ex convexa fit concava vel contra: cui negotio eleganter inservit doctrina de maximis et minimis, hoc prwmisso lemmate generali:
The above was posthumously printed in the Opera varia, Toulouse, 1679, and is also in Oeuvres de Fermat, Paris : Gauthier-Villars, 1891, p. 166).
The inflection point of this curve had been mentioned by Roberval in his letter to Fermat from 22 November, 1636 (printed in Oeuvres de Fermat - Supplément aux tomes I-IV, Paris, 1922, p. 44-45); Roberval writes concerning the conchoid:
vous treuverez qu'il y a un certain point en icelle comme B, tel que depuis A iusques en B, elle est convexe en dehors, et depuis B par C à l'infiny, elle est convexe en dedans, ce qui est admirable. Et encor plus que par le point B, il ne se peut mener de ligne droite qui la touche, mais une comme OBY, qui fera les angles au sommet OBA, YBC, chacun moindre qu'aucun angle rectiligne donne. Il en sera de mesme de l'autre part, et ce sont ces deux points d'où ie vous mandois qu'on ne pouvoit mener de tangentes. (p. 45)
Mesolabum, (2nd ed., 1668) by René François Walther de Sluze contains two additional parts, "De Analysi" and "Miscellanea." Chapter 5 of the Miscellanea, which has the title "De puncto flexus contrarii, in Conchoeide Nicomedis prima," answers a problem posed (and solved) by Christiaan Huygens (mentioned p. 119) at the end of his "De circuli magnitudine inventa," Leiden, 1654: problem VIII "In Conchoide linea invenire confinia flexus contrarii," p. 69-71 (with French translation and commentary in Huygens, Oeuvres complètes, vol. XII, 1910, p. 210-215; p. 110-112 give more detailed information on the interchange between Huygens and Schooten concerning this problem). The problem was later also solved by Hendrik van Heuraet, printed in Frans van Schooten’s "In Geometriam Renati Des Cartes Commentarii," 2nd edition, 1659, p. 258-262, where Schooten calls the point "punctum Conchoïdis C, quod duas ejus portiones, concavam & convexam, à se invicem distinguit."
The review of Sluse’s book in Philosophical Transactions, nr 45, (1669), p. 903-909, treats chapter 5 on p. 907 and quotes the title, but does not translate the term into English.
In the extract of Sluse’s famous letter on his tangent method, printed in Philosophical Transactions, nr 90, (1673), p. 5143-5147, Sluse refers to chapter 5 of the "Miscellanea": "qua ratione flexus contrarii curvarum ex Tangentibus inveniantur, ostendi" (p. 5147).
In his 1684 article "Nova methodus pro maximis et minimis" in Acta eruditorum, Leibniz used punctum flexus contrarii (point of opposite flection). More information is in T. F. Mulcrone, The Mathematics Teacher 61 (1968), 475-478, which has not been seen.
Newton used the term "point of straightness" to describe inflection points, according to the web page The History of Curvature.
Point of Inflection and point of inflexion are found in English in 1702 in A mathematical dictionary by Joseph Raphson, abridged from M. Ozanam and others. Page 16 has “point of Inflection of a Curve line” and page 17 has “Point of Inflexion of a Curve.”
In An Elementary Treatise on Curves, Functions and Forces (1846), Benjamin Peirce writes, "When a curve is continuous at a point, but changes its direction so as to turn its curvature the opposite way at this point, the point is called a point of contrary flexure, or a point of inflexion."
This entry was largely contributed by Siegmund Probst, who found the material on Fermat and Roberval in Cantor’s Vorlesungen über Geschichte der Mathematik.
INFLUENCE CURVE (in engineering) is found in 1902 in the article on “Bridges” in the 10th ed. of the Encyclopaedia Britannica. [Google print search by James A. Landau]
INFLUENCE CURVE (in robust statistical inference). The earliest JSTOR appearance of the term is in Peter J. Huber "The 1972 Wald Lecture Robust Statistics: A Review," Annals of Mathematical Statistics, 43, (1972), 1041-1067. Huber attributes the term to Frank R. Hampel. A little later Hampel’s "The Influence Curve and Its Role in Robust Estimation," Journal of the American Statistical Association, 69, (1974). 383-393 appeared.
INFORMATION, AMOUNT OF, QUANTITY OF in the theory of statistical estimation. R. A. Fisher first wrote about "the whole of the information which a sample provides" in 1920 ( Mon. Not. Roy. Ast. Soc., 80, 769). In 1922-5 he developed the idea that information could be given quantitative expression as minus the expected value of the second derivative of the log-likelihood. The formula for "the amount of information in a single observation" appears in the 1925 " Theory of Statistical Estimation.," Proc. Cambr. Philos. Soc. 22. p. 709. In the modern literature the qualification Fisher’s information is common, distinguishing Fisher’s measure from others originating in the theory of communication as well as in statistics. [John Aldrich and David (1995)].
INFORMATION, MEASURE OF in the theory of communication was introduced by Claude Shannon in his A Mathematical Theory of Communication (1948).
INFORMATION THEORY. The OED2 shows a number of citations for this term from 1950: e.g. W. G. Tuller in Trans. Amer. Inst. Electr. Engin. LXIX. 1612/1 "The statistical theory of communications, developed over the past few years and often called information theory, can be of real assistance in the design of communication systems." The theory alluded to was mainly the work of C. E. Shannon, in particular his A Mathematical Theory of Communication (1948).
See also BIT and ENTROPY.
INJECTION, SURJECTION and BIJECTION. The OED records a use of injection by S. MacLane in the Bulletin of the American Mathematical Society (1950) and injective in Eilenberg and Steenrod in Foundations of Algebraic Topology (1952). However the family of terms is introduced on p. 80 of Nicholas Bourbaki’s Théorie des ensembles, Éléments de mathématique Première Partie, Livre I, Chapitres I, II (1954). Reviewing the book in the Journal of Symbolic Logic, R. O. Gandy (1959, p. 72) wrote:
Another useful function of Bourbaki’s treatise has been to standardise notation and terminology… Standard terms are badly needed for “one-to-one,” “onto” and “one-to-one onto”; will Bourbaki’s “injection,” “surjection” and “bijection” prove acceptable?
The terms did prove acceptable, even to mathematicians writing in English, and quickly became standard. For instance, all three terms are used in Jun-Ichi Igusa “Fibre Systems of Jacobian Varieties,” American Journal of Mathematics, 78, (1956), 171-199. (JSTOR search) The adjectival forms appear in C. Chevalley, Fundamental Concepts of Algebra (1956): “A homomorphism which is injective is called a monomorphism; a homomorphism which is surjective is called an epimorphism.” (OED)
See the entries ONE-TO-ONE and ONTO and MONOMORPHISM.
The term INNER PRODUCT was coined (in German as inneres produkt) by Hermann Günther Grassman (1809-1877) in Die lineale Ausdehnungslehre (1844).
According to the OED2 it is "so named because an inner product of two vectors is zero unless one has a component 'within' the other, i.e. in its direction."
According to Schwartzman (p. 155):
When the German Sanskrit scholar Hermann Günther Grassman (1809-1877) developed the general algebra of hypercomplex numbers, he realized that more than one type of multiplication is possible. To two of the many possible types he gave the names inner and outer. The names seem to have been chosen because they are antonyms rather than for any intrinsic meaning.
In English, inner product is found in 1901 in An Elementary Exposition of Grassmann’s Ausdehnungslehre, or Theory of Extension by Jos. V. Collins, reprinted from the American Mathematical Monthly, Vols. VI and VII. [Google print search by James A. Landau]
The term INNUMERACY was popularized as the title of a recent book by John Allen Paulos. The word is found in 1959 in Rep. Cent. Advisory Council for Educ. (Eng.) (Ministry of Educ.): "If his numeracy has stopped short at the usual Fifth Form level, he is in danger of relapsing into innumeracy" (OED2).
INSTRUMENTAL VARIABLES in Econometrics and Statistics. The term first appeared in Olav Reiersøl’s "Confluence Analysis by Means of Instrumental Sets of Variables," Arkiv for Mathematik, Astronomi och Fysik, 32 (1945), 1-119. In an ET interview (p. 119) Reiersøl recalled that the name was suggested by his supervisor, Ragnar Frisch. Reiersøl had proposed the method already in 1941 and independently R. C. Geary proposed it in 1943. Reiersøl and Geary were interested in errors in variables models but around 1950 it became clear that their method could be applied to the recently developed SIMULTANEOUS EQUATIONS MODEL. Curiously the method had been used in the 1920s by the economist Phillip G. Wright and his geneticist son Sewall Wright for estimating demand functions but the method was not taken up and the work had no influence in Econometrics. The relative contribution of father and son has been a matter of controversy and Stock & Trebbi have discussed the issue quite recently.
(Based on J. Aldrich "Reiersøl, Geary and the Idea of Instrumental Variables," Economic and Social Review, 24, (1993), 247-274 pdf and J. H. Stock & F Trebbi "Who Invented IV Regression?" Journal of Economic Perspectives, 17, (2003), 177-194 pdf)
See the entries ERROR: ERRORS IN VARIABLES and PATH ANALYSIS.
INTEGER and WHOLE NUMBER. Writing in Latin, Fibonacci used numerus sanus.
According to Heinz Lueneburg, the term numero sano "was used extensively by Luca Pacioli in his Summa. Before Pacioli, it was already used by Piero della Francesca in his Trattato d'abaco. I also find it in the second edition of Pietro Cataneo’s Le pratiche delle due prime matematiche of 1567. I haven't seen the first edition. Counting also Fibonacci’s Latin numerus sanus, the word sano was used for at least 350 years to denote an integral (untouched, virginal) number. Besides the words sanus, sano, the words integer, intero, intiero were also used during that time."
The first citation for whole number in the OED2 is from about 1430 in Art of Nombryng ix. EETS 1922:
Of nombres one is lyneal, ano(th)er superficialle, ano(th)er quadrat, ano(th)cubike or hoole.In the above quotation (th) represents a thorn. In this use, whole number has the obsolete definition of "a number composed of three prime factors," according to the OED2.
Whole number is found in its modern sense in the title of one of the earliest and most popular arithmetics in the English language, which appeared in 1537 at St. Albans. The work is anonymous, and its long title runs as follows: "An Introduction for to lerne to reken with the Pen and with the Counters, after the true cast of arismetyke or awgrym in hole numbers, and also in broken" (Julio González Cabillón).
Oresme used intégral.
Integer was used as a noun in English in 1571 by Thomas Digges (1546?-1595) in A geometrical practise named Pantometria: "The containing circles Semidimetient being very nighe 11 19/21 for exactly nether by integer nor fraction it can be expressed" (OED2).
Integral number appears in 1658 in Phillips: "In Arithmetick integral numbers are opposed to fraction[s]" (OED2).
Whole number is most frequently defined as Z+, although it is sometimes defined as Z. In Elements of the Integral Calculus (1839) by J. R. Young, the author refers to "a whole number or 0" but later refers to "a positive whole number."
INTEGRABLE is found in English in 1727-41 in Chambers' Cyclopaedia (OED2).
Integrable is also found in 1734 in An Examination of Dr. Burnet’s Theory of the Earth by John Keill and Maupertuis. [Google print search]
The word INTEGRAL first appeared in print by Jacob Bernoulli (1654-1705) in May 1690 in Acta eruditorum, page 218. He wrote, "Ergo et horum Integralia aequantur" (Cajori vol. 2, page 182; Ball). According to the DSB this represents the first use of integral "in its present mathematical sense."
However, Jean I Bernoulli (1667-1748) also claimed to have introduced the term. According to Smith (vol. I, page 430), "the use of the term 'integral' in its technical sense in the calculus" is due to him.
The following terms to classify solutions of nonlinear first order equations are due to Lagrange: complete solution or complete integral, general integral, particular case of the general integral, and singular integral (Kline, page 532).
INTEGRAL CALCULUS. Leibniz originally used the term calculus summatorius (the calculus of summation) in 1684 and 1686.
Johann Bernoulli introduced the term integral calculus.
Cajori (vol. 2, p. 181-182) says:
At one time Leibniz and Johann Bernoulli discussed in their letters both the name and the principal symbol of the integral calculus. Leibniz favored the name calculus summatorius and the long letter [long S symbol] as the symbol. Bernoulli favored the name calculus integralis and the capital letter I as the sign of integration. ... Leibniz and Johann Bernoulli finally reached a happy compromise, adopting Bernoulli’s name "integral calculus," and Leibniz' symbol of integration.According to Smith (vol. 2, page 696), Leibniz in 1696 adopted the term calculus integralis, already suggested by Jacques Bernoulli in 1690.
According to Stein and Barcellos (page 311), the term integral calculus is due to Leibniz.
The term "integral calculus" was used by Leo Tolstoy in Anna Karenina, in which a character says, "If they'd told me at college that other people would have understood the integral calculus, and I didn't, then ambition would have come in."
INTEGRAL DOMAIN is found in 1907 in Synopsis of Linear Associative Algebra by James Byrnie Shaw. [Google print search by James A. Landau]
INTEGRAL EQUATION. According to Kline (p. 1052) and J. Dieudonné History of Functional Analysis (p. 97), the term integral
equation (Integralgleichung)
is due to Paul du Bois-Reymond (1831-1889). Du Bois-Reymond introduced it in
his paper on the DIRICHLET
PROBLEM, “Bemerkungen über 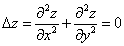 ,”
Journal
für die reine und angewandte Mathematik, 103, (1888), 204-229.
Integral equations became a very hot topic at the beginning of the 20th century with influential contributions from E. Fredholm,
“Sur une classe des équations fonctionnelles,” Acta Mathematica, 27,
(1903), 365–390, and from D. Hilbert whose articles of 1904-6 were
collected into a book, Grundzüge einer
allgemeinen Theorie der linearen Integralgleichungen (1912).
Hilbert’s work played a critical part in the rise of FUNCTIONAL ANALYSIS.
See the Encyclopaedia of Mathematics entry Integral equations.
,”
Journal
für die reine und angewandte Mathematik, 103, (1888), 204-229.
Integral equations became a very hot topic at the beginning of the 20th century with influential contributions from E. Fredholm,
“Sur une classe des équations fonctionnelles,” Acta Mathematica, 27,
(1903), 365–390, and from D. Hilbert whose articles of 1904-6 were
collected into a book, Grundzüge einer
allgemeinen Theorie der linearen Integralgleichungen (1912).
Hilbert’s work played a critical part in the rise of FUNCTIONAL ANALYSIS.
See the Encyclopaedia of Mathematics entry Integral equations.
Although du Bois-Reymond introduced the term in its modern sense, Euler had earlier used a phrase which is translated integral equation in the paper “De integratione aequationis differentialis,” Novi Commentarii Academiae Scientarum Petropolitanae 6, 1756-57 (1761). Integral equation is found in English in 1802 in Woodhouse, Phil. Trans. XCII. 95: “Expressions deduced from the true integral equations.” (OED).
[This entry was contributed by John Aldrich. James A. Landau provided a citation.]
The term INTEGRAL GEOMETRY is due to Wilhelm Blaschke (1885-1962), according to the University of St. Andrews website.
INTEGRAND (in logic). Sir William Hamilton of Scotland used this word in logic. It appears in his Lectures on metaphysics and logic (1859-1863): "This inference of Subcontrariety I would call Integration, because the mind here tends to determine all the parts of a whole, whereof a part only has been given. The two propositions together might be called the integral or integrant (propositiones integrales vel integrantes). The given proposition would be styled the integrand (propositio integranda); and the product, the integrate (propositio integrata)" [University of Michigan Digital Library].
INTEGRAND (in calculus) is found in 1827 in Bündige und reine Darstellung des wahrhaften Infinitesimal-Calculs by Friedrich Gottlieb von Busse. [Google print search by James A. Landau]
INTEGRATING FACTOR is found in 1832 in A Treatise on Differential Equations by W. C. Ottley. [Google print search by James A. Landau]
INTEGRATION BY PARTS is found in 1804 in Transactions of the Cambridge Philosophical Society. [Google print search by James A. Landau]
The method was invented by Brook Taylor and discussed in Methodus incrementorum directa et inversa (1715).
INTEGRATION BY SUBSTITUTION is found in 1837 in The Theory of the Differential and Integral Calculus by John Forbes: “The general principle of the Integral Calculus is extended by means of these different modes, to the integration of complex functions, both rational and surd; viz. integration by substitution, integration by analysis, and integration by parts, or, as it is sometimes termed, successive integration.” [Google print search by James A. Landau]
INTERIOR ANGLE is found in English in 1629 in “A treatise of artificial fire-vvorks both for vvarres and recreation with divers pleasant geometricall obseruations, fortifications, and arithmeticall examples by Francis Malthus. [Google print search by James A. Landau]
INTERMEDIATE VALUE THEOREM. Theorem of intermediate value is found in English in 1902 in the 10th ed. of the Encycopaedia Britannica in the article “Functions of Real Variables.” [Google print search by James A. Landau]
Intermediate value theorem appears in 1927 in The Mathematics of Engineering by Ralph Eugene Root. [Google print search]
The term INTERPOLATION was introduced into mathematics by John Wallis (DSB; Kline, page 440).
The word appears in the English translation of Wallis' algebra (translated by Wallis and published in 1685), although the use that has been found in the excerpt in Smith’s Source Book in Mathematics appears not to be his earliest use of the term.
For some of the pre-history (and post-history) of interpolation see Erik Meijering A Chronology of Interpolation: From Ancient Astronomy to Modern Signal and Image Processing Proceedings of the IEEE, 90, 319-342.
INTERQUARTILE RANGE is found in 1882 in Francis Galton, "Report of the Anthropometric Committee," Report of the 51st Meeting of the British Association for the Advancement of Science, 1881, pp. 245-260: "This gave the upper and lower 'quartile' values, and consequently the 'interquartile' range (which is equal to twice the 'probable error') (OED2).
INTERSECTION (in set theory) is found in Webster’s New International Dictionary of 1909.
INTO is used in the sense of a mapping in 1949 by Solomon Lefschetz, Introduction to Topology (OED).
INTRINSICALLY CONVERGENT SEQUENCE (Cauchy sequence) is apparently found in 1935 in Abstracts of Doctoral Dissertations of the Ohio State University. [Google print search by James A. Landau]
The term INTRINSIC EQUATION was introduced in 1849 by William Whewell (1704-1886) (Cajori 1919, page 324).
INTUITIONISM in the philosophy of mathematics. The term entered the English mathematical vocabulary with L. E. J. Brouwer’s inaugural lecture of 1912, which appeared in English as "Intuitionism and Formalism," Bull. Amer. Math. Soc. 20, (1913), 81-96. There Brouwer wrote
On what grounds the conviction of the unassailable exactness of mathematical laws is based has for centuries been an object of philosophical research, and two points of view may here be distinguished, intuitionism (largely French) and formalism (largely German). ... The question where mathematical exactness does exist, is answered differently by the two sides; the intuitionist says: in the human intellect, the formalist says: on paper. (pp. 82-3, OED)
See Brouwer in MacTutor and Brouwer in the Stanford Encyclopedia. See also the entries FORMALISM and LOGICISM.
The term INVARIANT was coined by James Joseph Sylvester. It appears in 1851 in "On A Remarkable Discovery in the Theory of Canonical Forms and of Hyperdeterminants," Philosophical Magazine, 4th Ser., 2, 391-410: "The remaining coefficients are the two well-known hyperdeterminants, or, as I propose henceforth to call them, the two Invariants of the form ax4 + 4bx3y + 6cx2y2 + 4dxy3 + ey4." In the same article he wrote, "If I (a, b,..l) = I (a', b',..l'), then I is defined to be an invariant of f."
See also normal subgroup.
INVERSE (element producing identity element) appears in 1900 in James Pierpont "Galois' Theory of Algebraic Equations. Part II. Irrational Resolvents," Annals of Mathematics. p. 48 "For every element Tκ exists an element (denote it by Tκ-1) such that Tκ Tκ-1 = Tκ-1 Tκ = 1. Tκ-1 is called the inverse of Tκ " (OED2).
INVERSE (in logic) is found in 1890 in Elements of Logic as a Science of Propositions by Emily Elizabeth Constance Jones. [Google print search by James A. Landau]
INVERSE of a matrix. In his fundamental work of 1858 "A Memoir on the Theory of Matrices" Arthur Cayley introduced two terms for L-1, "or as it may be termed the inverse or reciprocal matrix." Coll Math Papers, I, 480. Writers in English long preferred the term reciprocal matrix: see e.g. the famous textbook by A. C. Aitken, Determinants and Matrices (1st edition 1939, 9th edition 1956). However that term has disappeared and inverse matrix is now universal. This usage is more in line with that in abstract algebra.
See MATRIX and GENERALIZED INVERSE.
INVERSE FUNCTION appears in in English in 1816 in the translation of Lacroix’s Differential and Integral Calculus: "ex and log x are inverse functions of each other since log (ex) = x" (OED2).
The term INVERSE GAUSSIAN DISTRIBUTION is found in M. C. K. Tweedie (1947) "Functions of a Statistical Variate with Given Means, with Special Reference to Laplacian Distributions," Proceedings of the Cambridge Philosophical Society, 43, 41-49. [Gerard Letac]
See also GAUSSIAN.
INVERSE PROBABILITY. From the time of Augustus De Morgan’s Essay on Probabilities (1838) until that of Harold Jeffreys’s Theory of Probability (1939) English works on probability distinguished between direct and inverse probabilities. De Morgan (p. 53) distinguished between the two, "we have calculated the chances of an event, knowing the circumstances under which it is to happen or fail. We are now to place ourselves in an inverted position: we know the event, and ask what is the probability which results from the event in favour of any set of circumstances under which the same might have happened." The alternative "sets of circumstances" were usually called "causes" or "hypotheses" and so the domain of inverse probability was the probability of causes or what would now be called Bayesian probability. However the new Bayesian writers of the 1960s discarded the direct and inverse terms and these have fallen out of use.
A. I. Dale reports a much earlier use of the phrase "méthode inverse des probabilités" in an outline Fourier wrote for some lectures given at the École Polytechnique in Paris in the late 18th or early 19th century. (A History of Inverse Probability from Thomas Bayes to Karl Pearson.)
This entry was contributed by John Aldrich. See BAYES and POSTERIOR PROBABILITY.
INVERSE VARIATION. Inverse ratio and inversely are found in English in 1660 in Barrow’s translation of Euclid.
Inverse proportion is found in English in 1648 in The construction and use of the logarithmeticall Tables by Edmund Wingate: “Probl. IV. Having three numbers given, to finde a fourth in an inverse proportion.” [Google print search by James A. Landau]
Inversely proportional is found in English in 1741 in a translation of Euclid by Dr. John Keil: “Coroll. From hence it is manifest, if four Magnitudes be proportional, that they will be also inversely proportional.” [Google print search by James A. Landau]
Varies inversely is found in 1789 in A System of Mechanics and Hydrostatics by Rev. T. Parkinson: “Cor. 4. The latitude of a pulse [of sound] varies inversely as the number of vibrations of the sounding body in a given time, or directly as the time of one vibration. . . .” [Google print search by James A. Landau]
Inverse variation is found in 1830 in The Edinburgh Review, or Critical Journal: For April-July, 1830. “The law of inverse variation, or inverse proportion, is a much a part of mathematical science as the law of geometric progression. The only difference in this respect between Mr Malthus and Mr Sadler is, that Mr Malthus knows what is meant by geometric progression, and that Mr Sadler has not the faintest notion of what is meant by inverse variation. Had he understood the proposition which he has enounced with so much pomp, its ludicrous absurdity must at once have flashed on his mind.” [Google print search by James A. Landau].
The INVERTED GAMMA DISTRIBUTION is found in Howard Raiffa & Robert Schlaiffer’s Applied Statistical Decision Theory (1961, p. 227).
See also GAMMA DISTRIBUTION.
The term INVOLUTION is due to Gérard Desargues (1593-1662) (Kline, page 292).
IRRATIONAL. See RATIONAL AND IRRATIONAL.
IRREDUCIBLE INVARIANT is found in 1856 in “A Second Memoir upon Quantics” by Arthur Cayley in the Philosophical Transactions. [James A. Landau]
ISOGON is a rare term for an equiangular polygon. The OED shows it in 1696 in the fifth edition of Edward Phillips' dictionary, where it is spelled isagon.
ISOGRAPHIC is the word used by Ernest Jean Philippe Fauquede Jonquiéres (1820-1901) to describe the transformations he had discovered, later called birational transformations (DSB).
ISOMERIA is a term used by Vieta for freeing an equation of any fractions by multiplying both sides by the least common denominator. The word is found in English in 1696 in Edward Phillips' dictionary.
ISOMETRY. Aristotle used the word isometria.
Isometry is found in English in Appletons' Cyclopaedia of Drawing edited by W. E. Worthen, which is dated 1857 but appears to be cited in a catalog printed in 1853 [University of Michigan Digital Library].
In its modern sense, isometry occurs in English in 1941 in Survey of Modern Algebra by MacLane and Birkhoff: "An obvious example is furnished by the symmetries of the cube. Geometrically speaking, these are the one-one transformations which preserve distances on the cube. They are known as 'isometries,' and are 48 in number" (OED).
ISOMORPHIC, ISOMORPHISM. The term isomorphism was used early in crystallography. Some books on geology before 1864 referred to “geometrical isomorphism” or “mathematical isomorphism” between crystals.
Isomorphic was used by J. J. Sylvester in 1864 in “The Real And Imaginary Roots Of Algebraical Equations: A Trilogy,” in the Philosophical Transactions:
To every point in space, it has been remarked, will correspond one particular family of equations all of the same character as regards the number they contain of real or imaginary roots, because capable of being derived from one another by real linear substitutions, such family consisting of an infinite number of ordinary or conjugate equations according as the point is facultative or non-facultative; but it may be well to notice that, conversely, every point does not correspond to a distinct family. In fact every point in the curves D = pJ 2, L = qJ 2 (p, q being constants) will denote a curve divided into two branches by the origin of coordinates, one of which will be facultative and the other non-facultative; but in each separate branch every point will represent the very same family. Any such separate branch may be termed an isomorphic line; and we see that the whole of space may be conceived as permeated by and made up of such lines radiating out from the origin in all directions.
In 1870 Traité Des Substitutions Et Des Équations Algébriques by Camille Jordan has (p. 56):
67. Un groupe Γ est dit isomorphe à un autre groupe G, si l'on peut établir entre leurs substitutions une correspondance telle : i° que chaque substitution de G corresponde à une seule substitution de Γ, et chaque substitution de Γ à une ou plusieurs substitutions de G; 2° que le produit de deux substitutions quelconques de G corresponde au produit de leurs correspondantes respectives. [Google print search]
A translation is: “A group Γ is called “isomorphic” to another group G, if one can establish between their substitutions a correspondence such that: i° each substitution of G corresponds to a single substitution of Γ, and each substitution of Γ to one or more substitutions of G, 2° the product of any two substitutions of G corresponds to the product of their respective corresponding substitutions.”
Isomorphism was used by Walter Dyck (1856-1934) in 1882 in Gruppentheoretische Studien (Katz, page 675).
This entry was contributed by James A. Landau.
ISOSCELES. The isosceles triangle is treated in
Euclid’s Elements XIII. xvi.
The word is formed from 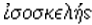 equal-legged from
equal-legged from 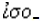 +
+ 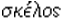 ,
, 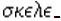 leg.
The word appears in English in Billingsley’s
translation of Euclid I. Def. xxv. 5 “Isosceles, is
a triangle, which hath onely two sides equall.”
leg.
The word appears in English in Billingsley’s
translation of Euclid I. Def. xxv. 5 “Isosceles, is
a triangle, which hath onely two sides equall.”
A few years before, Recorde had introduced an English expression in The Pathwaie to Knowledge: “There is also an other distinction of the name of triangles, according to their sides, whiche other be all equal...other els two sydes bee equall and the thyrd vnequall, which the Greekes call Isosceles, the Latine men aequicurio, and in english tweyleke [= two-like] may they be called.” See the entry EQUILATERAL for further discussion.
Billingsley adopted the Greek word but there was also a Latin word. The OED reports an isosceles triangle being called an equicrure in 1644 (this usage it describes as obsolete) and an equicrural triangle in 1650. These are the earliest uses it gives for the terms of Latin origin.
The term ITERATED FUNCTION SYSTEM was coined by Michael Barnsley, according to an Internet website. According to Wikipedia, IFSs were conceived in their present form by John E. Hutchinson in 1981 and popularized by Michael Barnsley’s book Fractals Everywhere (1988).