meaning a bulging, convexity.
meaning a bulging, convexity.
See also CUMULANT.
K-THEORY. The term came into use around 1960. It appears in a Mathematics Review article by R. Bott on M. F. Atiyah & F. Hirzebruch “Vector bundles and homogeneous spaces,” 1961 Proc. Sympos. Pure Math., Vol. III, pp. 7-38. Bott writes, “This paper summarizes some of the authors’ researches on the K-theory …” See the Encyclopedia of Mathematics entry K-theory.
KALMAN FILTER refers to the method introduced by R. E. Kalman in his A New Approach to Linear Filtering and Prediction Problems, Transactions of the ASME - Journal of Basic Engineering Vol. 82: pp. 35-45 (1960) See here for the paper. S. L. Lauritzen argues in his 2002 book Thiele: Pioneer in Statistics that Thiele anticipated Kalman by 80 years. In the 1820s Gauss had devised up-dating formulae for least squares estimates. [John Aldrich]
See FILTER.
The KAPLAN-MEIER estimator was proposed by E. L. Kaplan and Paul Meier in “Nonparametric Estimation from Incomplete Observations,” Journal of the American Statistical Association, 53, (1958), 457-481. Meier recalled the collaboration to Harry Marks in “A Conversation with Paul Meier,” Clinical Trials, 1, (2004), 131-138. The Kaplan-Meier paper is one of the most cited in biostatistics: an early reference to the “Kaplan-Meier method” is in H. F. Stein “Disseminated Coccidioidomycosis,” Diseases of the Chest, 36, (1959), 136-145.
KERNEL. Ivar Fredholm used the French word, “noyau,” in his famous paper on INTEGRAL EQUATIONS, “Sur une classe des équations fonctionnelles,” Acta Math., 27, (1903), 365–390. David Hilbert put this into German as Kern in his “Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen,” Nachrichten von d. Königl. Ges. d. Wissensch. zu Göttingen (Math.-physik. Kl.) (1904) p. 49. The English word kernel appears in M. Bôcher’s Introduction to the Study of Integral Equations (1909): “K is called the kernel of these equations.” (quoted in the OED). See G. Birkhoff & E. Kreyszig (1984) “The Establishment of Functional Analysis,” Historia Mathematica, 11, 258-321.
Kernel was an established term in Fourier analysis by the time of A. Zygmund’s Trigonometrical Series (1935). A JSTOR search found the "Fejér kernel" and "Dirichlet kernel" in Charles N. Moore’s "On the Application of Borel’s Method to the Summation of Fourier’s Series" (Proceedings of the National Academy, 11, (1925), 284-287) but it is unlikely that this was the first published use of these terms.
Kernel entered Statistics with the use of Fourier theory in describing estimates for spectral density and probability density functions. A JSTOR search found E. F. Schuster (Annals of Mathematical Statistics, 40, (1969), p. 1187) referring to "a so-called kernel class of estimates," introduced by M. Rosenblatt in "Remarks on Some Nonparametric Estimates of a Density Function," Annals of Mathematical Statistics, 27, (1956), 832-837. Earlier "Fejér kernel" was used in U. Grenander & M.Rosenblatt’s "Statistical Spectral Analysis of Time Series Arising from Stationary Stochastic Processes," Annals of Mathematical Statistics, 24, (1953), 537-558. An alternative term, especially popular in time series analysis, is WINDOW.
See also FEJÉR KERNEL.
The use of kernel in algebra appears to be unrelated to its use in integral equations and Fourier analysis. L. Pontrjagin used the term in 1931 on page 102 of his paper “Über den algebraischen Inhalt topologischer Dualitätssätze” in Math. Annalen 105.
The OED gives the following quotation from Pontrjagin’s Topological Groups i. 11 (translated by E. Lehmer 1946) "The set of all the elements of the group G which go into the identity of the group G* under the homomorphism g is called the kernel of this homomorphism."
G. D. Birkhoff & S. A. MacLane A Survey of Modern Algebra 3rd edition 1965, pp. 213-4 apply the concepts of homomorphism and kernel to a linear transformation T between vector spaces considered as an Abelian Group under addition. They remark, “Since O is the group identity, it follows that that the null-space of T is precisely the kernel of T regarded as a group-homomorphism.” See the entry NULL SPACE.
[John Aldrich, Jan Peter Schäfermeyer]
KITE. Deltoid appears in 1879 in Dictionary of Scientific Terms: "Deltoid, a four-sided figure formed of two unequal isosceles triangles on opposite sides of a common base" (OED2).
Kite appears as a geometric term in the 1893 Funk and Wagnalls Standard Dictionary.
KLEIN BOTTLE is found in 1940 in W. T. Puckett, "On 0-Regular Surface Transformations," Trans. American Mathematical Society [John M. Sullivan].
Klein bottle occurs in C. Tompkins, "A flat Klein bottle isometrically embedded euclidean 4-space," Bull. Am. Math. Soc. 47, 508 (1941).
Felix Klein describes--but does not illustrate--the construction in his short book Ueber Riemann’s theorie der algebraischen functionen und ihrer integrale (1882) reprinted in Ges. Math. Abh, 3, 499-573.
KLEIN FOUR GROUP. Vierergruppe is found in 1884 in Vorlesungen uber das Ikosaeder und die Aufloesung der Gleichungen vom funften Grade by Felix Klein:
Offenbar umfasst unsere neue Gruppe von der Identitaet abgesehen nur Operationen von der Periode 2, und es ist zufaellig, das wir eine dieser Operationen an die Hauptaxe der Figur, die beiden anderen an die Nebenaxe geknupft haben. Dementsprechend will ich die Gruppe mit einem besonderen Namen belegen, der nicht mehr and die Dieder- configuration erinnert, und sie als Vierergruppe benennen.The above citation was provided by Gunnar Berg.
The term "(Kleinsche) Vierergruppe" was used by Bartel Leendert van der Waerden (1903-1996) in 1930 in his influential textbook Moderne Algebra. It denotes the permutation group generated by (12)(34) and (13)(24), rather than the abstract product of two 2-cyclic groups. The term does not occur in the older algebra books by Weber and by Perron [Peter Flor].
In English, “the Klein linear group of order 4 !” is found in 1898 in Science: A Weekly Journal devoted to the advancement of science. [Google print search by James A. Landau]
The term KLEINIAN GROUP was used by Henri Poincaré.
Kleinian group is found in 1891 in “On a Classs of Automorphic Functions” by W. Burnside in Proceedings of the London Mathematical Society: “In this paper I shall adhere as closely as possible to the notation and nomenclature used by M. Poincaré. ... Hence this second proof certainly establishes the existence of Kleinian groups of the kind considered ....” [Google print search by James A. Landau]
KNOT. The first mathematical paper which mentions knots is "Remarques sur les problemes de situation" (1771) by Alexandre-Theophile Vandermonde (1735-1796).
KNOT THEORY. Theory of knots is found in 1911 in the Encyclopaedia Britannica, 11th ed. “The founder of the theory of knots is undoubtedly Johann Benedict Listing (1808-1882).” [Google print search by James A. Landau]
Knot theory appears in 1932 in the title Knotentheorie by Kurt Werner Friedrick Reidemeister (1893-1971).
KOLMOGOROV EXTENSION THEOREM refers to the theorem in Section 4 of Chapter III of A. N. Kolmogorov’s Grundbegriffe der Wahrscheinlichkeitsrechnung (1933). (English translation) It is also called the Daniell-Kolmogorov theorem in recognition of the work of P. J. Daniell, "Integrals in an Infinite Number of Dimensions," Annals of Mathematics, 20, (1919) 281-88.
The relationship between the work of Kolmogorov and Daniell is discussed by Glenn Shafer and Vladimir Vovk "The Sources of Kolmogorov’s Grundbegriffe," Statist. Sci. 21, (2006), 70-98 section 5.1.2.
KOLMOGOROV FORWARD AND BACKWARD EQUATIONS. See the entry FOKKER-PLANCK EQUATION.
KOLMOGOROV-SMIRNOV TEST appears in F. J. Massey Jr., "The Kolmogorov-Smirnov test of goodness of fit," J. Amer. Statist. Ass. 46 (1951).
See also W. Feller, "On the Kolmogorov-Smirnov limit theorems for empirical distributions," Ann. Math. Statist. 19 (1948) [James A. Landau].
The references are to A. N. Kolmogorov "Sulla determinazione empirica di una legge di distribuzione," Inst. Ital. Attuari, Gorn., 4, (1933), 1-11 and V. I. Smirnov (1900-66) "On the estimation of the discrepancy between empirical curves of distribution for two independent samples," Bulletin Mathématique de l’Université de Moscou, 2, (1939), fasc. 2.
KÖNIGSBERG BRIDGE PROBLEM. The problem was posed and solved in L. Euler "Solutio problematis ad geometriam situs pertinentis" (The solution of a problem relating to the geometry of position) Comment. Acad. Sci. U. Petrop. 8, 128-140, 1736. Reprinted in Opera Omnia Ser. I-7, pp. 1-10, 1766. There is an English translation in James Newman World of Mathematics vol. 1. 573-580. See also MacTutor History of Topology
See the entries GRAPH and TOPOLOGY.
KRIGING refers to a family of least squares techniques for spatial data first developed by Daniel Gerhardus Krige in his Master’s thesis at the University of Witwatersrand, A Statistical Approach to Some Mine Valuations and Allied Problems at the Witwatersrand (1951). The eponym krigeage was coined by Georges Matheron and appeared in his Krigeage d’un Panneau Rectangulaire par sa Périphérie (1960). The term went into English as kriging and from the geological literature into the statistical literature where it has been established since the 1970s.
It is found in 1970 in Random kriging in Geostatistics — A colloquium by A. Marechal and J. Serra. [Google print search by James A. Landau]
See the Wikipedia entry Kriging.
The term KRONECKER DELTA is found in 1926 in Riemannian Geometry by Luther Pfahler Eisenhard: "These are called the Kronecker deltas and are used frequently throughout this work." The term is used because Kronecker used the construction in his lectures. [Joanne M. Despres of Merriam-Webster Inc.]
The KRONECKER, ZEHFUSS or DIRECT PRODUCT of matrices. In their article “On the history of the kronecker product” Linear and Multilinear Algebra, 14, (1983), 113 – 120, H. V. Jemderson, F. Pukelsheim & S. R. Searle find the origins of such products in a paper on determinants by Johann Georg Zehfuss “Ueber eine gewisse Determinante,” Zeitschrift für Mathematik und Physik, 3, (1858), 298-301. The link to Kronecker was made by K. Hensel, “Ueber Gattungen, welche durch Composititon aus zwei anderen Gattungen entstehen” Journal für die reine und angewandte Mathematik, 105, (1899), 329-344 who held that Kronecker discussed them in his lectures in the 1880s.
When the products entered the English literature in the 1930s A. C. Aitken “The Normal Form of Compound and Induced Matrices,” Proceedings of the London Mathematical Society, 38, (1935) 354 – 376 called them Zehfuss products, F.D. Murnaghan Theory of Group Representations (1938, p. 68) called them Kronecker products while C. C. MacDuffee, The Theory of Matrices, Springer (1933) referred to direct products. MacDuffee (p. 82) explains “The concept of direct product of matrices arises naturally from the concept of direct product in group theory.” For the latter he refers to O. Hölder “Die Gruppen der Ordnungen p3, pq2, pqr, p4,” Mathematische Annalen, 43, (1893), p. 305. [John Aldrich]
KRONECKER’S JUGENDTRAUM. In a letter to Dedekind of 1880 Leopold Kronecker refers to meinen liebsten Jugendtraum (the dearest dream of my youth): see Kronecker Werke V p. 455. The passage reads in translation:
It concerns the dearest dream of my youth, namely to prove that abelian equations with square-roots-rational numbers are reduced to transformation-equations of elliptic functions with singular moduli, just as integral abelian equations to cyclotomic equations.
from S. G. Vladut Kronecker’s Jugendtraum and Modular Functions p. 79. The Jugendtraum is part of the background to Hilbert’s 12th problem. See N. Schappacher “On the History of Hilbert’s Twelfth Problem: A Comedy of Errors,” Matériaux pour l'histoire des mathématiques au XXième siècle (Nice, 1996), 243-273. pdf
See HILBERT’S PROBLEMS.
KUHN-TUCKER THEOREM, MULTIPLIER, etc. derive from H. W. Kuhn & A. W. Tucker’s "Nonlinear Programming", in J. Neyman, editor, Proceedings of the Second Berkeley Symposium (1951). T. H. Kjeldsen writes, "When Kuhn and Tucker proved the Kuhn-Tucker theorem ... they launched the theory of nonlinear programming. However, in a sense this theorem had been proven already: In 1939 by W. Karush in a master’s thesis, which was unpublished; in 1948 by F. John in a paper that was at first rejected by the Duke Mathematical Journal; and possibly earlier by Ostrogradsky and Farkas." ("A Contextualized Historical Analysis of the Kuhn-Tucker Theorem in Nonlinear Programming: The Impact of World War II," Historia Mathematica, 27, (2000), 331-361)
A JSTOR search found the terms Kuhn-Tucker theorem and Kuhn-Tucker conditions in circulation by the end of the 1950s and Kuhn-Tucker multipliers by the end of the 60s.
KULLBACK-LEIBLER INFORMATION (NUMBER) appears in Herman Chernoff "Large-Sample Theory: Parametric Case," Annals of Mathematical Statistics, 27, (1956), 1-22. The reference is to S. Kullback and R. A. Leibler "On Information and Sufficiency," Annals of Mathematical Statistics, 22, (1951), pp. 79-86. (JSTOR)
KURTOSIS was used by Karl Pearson in
1905 in "Das Fehlergesetz und seine Verallgemeinerungen durch Fechner und
Pearson. A Rejoinder," Biometrika,
4, 169-212, in the phrase
"the degree of kurtosis." He states therein that he has used the term
previously (OED). According to the OED and to Schwartzman the
term is based on the Greek  meaning a bulging, convexity.
meaning a bulging, convexity.
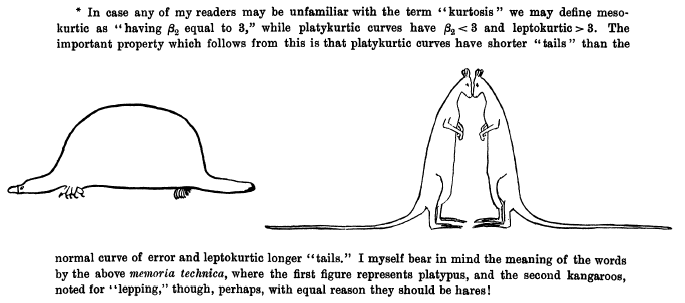
He introduced the terms leptokurtic, platykurtic and mesokurtic, writing in Biometrika (1905), 5. 173: "Given two frequency distributions which have the same variability as measured by the standard deviation, they may be relatively more or less flat-topped than the normal curve. If more flat-topped I term them platykurtic, if less flat-topped leptokurtic, and if equally flat-topped mesokurtic" (OED2).
In his "Errors of Routine Analysis" Biometrika, 19, (1927), p. 160 Student provided a mnemonic: