Earliest Known Uses of Some of the Words of Mathematics (E)
Last revision: June 23, 2017
ECCENTRICITY. Eccentric was a technical term in the
astronomical system of
Claudius Ptolemy. The English
word comes via Latin from the Greek ekkentros for “out
of the center” as opposed to concentric.
The earliest quotation in the OED is from 1398 but another quotation from
1561 better conveys the Ptolemaic meaning: “Eccentricke, is a circle
which hath his center distant… from the center of the worlde.”
Eccentricity appears in English in “A direct and Geometrical method for
finding the Aphelions, Eccentricities and proportions of the Orbs of the
primary Planets, without supposing the Equality of the Angle of motion
at the other Focus of the Planets Ellipsis, by Mr. Halley” in
Philosophical Transactions of the Royal Society, number 128, September
25, 1676. The above text appears on page 679 and is the journal’s
translation of the title of a Latin paper by Edmund Halley which appears
on page 683. The Latin title, as best as I can transcribe it, is “Methodus directa &
Geometrica, cujus ope investigantur Aphelia, Eccentricitates,
Proportionesque orbium Planetarum primariorum, absque supposita
aequalitate anguli motus, ad alterum Ellipseus focum, ab Astronomis
hactenus usurpati.” [James A. Landau]
ECONOMETRICS. In the editorial in the first issue of the
journal Econometrica, the organ of the Econometric Society,
Ragnar Frisch,
explained econometrics by referring to the aims of the Society: "Its
main object shall be to promote studies that aim at a unification of the theoretical-quantitative
and the empirical-quantitative approach to economic problems and that are penetrated
by constructive and rigorous thinking similar to that which has come to dominate
in the physical sciences. ... The mutual penetration of quantitative economic
theory and statistical observation is of the essence of econometrics." Econometrica, 1,
(1933), pp. 1-2. Frisch had already used the French version of the name, "l’économétrie,"
with the same meaning in a 1926 paper "Sur un problème d’économie pure." Earlier
appearances have been found, e.g. in German "Oekonometrie"
from 1910, but the word was not used in the sense that Frisch gave it. Equally,
modern contributors to econometrics have not always shared Frisch’s vision
of the subject.
EDGE (of a polyhedron). Euler used the Latin word acies. In a letter to Goldbach in 1750,
he described "the junctures where two faces come together
along their sides, which, for lack of an accepted term, I call acies." Acies is a Latin term which is comonly
used for the sharp edge of a weapon, a beam of light, or an army lined up for battle.
[Dave Richeson]
EDGEWORTH EXPANSION, SERIES, etc. derive from
F. Y. Edgeworth
"The Law of Error," Transactions of the Cambridge Philosophical
Society, 20, (1905) 36-65, 113-141. The term "Edgeworth’s series"
appears in E. P. Elderton’s review of Edgeworth’s paper (and some publications
by C. V. Charlier), which appeared in Biometrika, 5, (1906), 206-210.
In the 1920s H. Cramér developed a rigorous theory of "Edgeworth series" which
he summarised in his Random Variables and Probability Distributions (1937).
More recently the term "Edgeworth expansion" has come into circulation. A JSTOR
search found this in S. T. David, M. G. Kendall & A. Stuart "Some Questions
of Distribution in the Theory of Rank Correlation," Biometrika,
38, (1951), 131-140.
EFFECTS in the analysis of variance and experimental design. David (2001) traces
the terms row effect, column effect and treatment effect
to S. S. Wilks Mathematical Statistics (1943, p. 187). The term treatment
effect was in use earlier, e.g. in J. O. Irwin "On
the Independence of the Constituent Items in the Analysis of Variance," Supplement
to the Journal of the Royal Statistical Society, Vol. 1, No. 2. (1934),
pp. 236-251. The underlying concepts are implicit in Fisher’s earliest work--from
1923--on the analysis of variance.
See VARIANCE.
EFFICIENCY. The terms efficiency and efficient applied to estimation
were introduced by R. A. Fisher in
"On the Mathematical
Foundations of Theoretical Statistics" (Phil. Trans. R. Soc. 1922). He described
the criterion of efficiency as "satisfied by those statistics which, when
derived from large samples, tend to a normal distribution with the least possible
standard deviation." (p. 310) He also wrote: "To calculate the efficiency
of any given method, we must therefore know the probable error of the statistic
calculated by that method, and that of the most efficient statistic which could
be used. The square of the ratio of these two quantities then measures the efficiency."
(p. 316) In the later literature Fisher’s concept would be described as asymptotic
efficiency. Fisher did his first efficiency calculations in
A Mathematical Examination
of the Methods of Determining the Accuracy of an Observation by the Mean Error, and by the Mean Square Error
(1920) unaware that Gauss had done similar calculations
(Bestimmung der Genauigkeit der Beobachtungen
(1816)) a century earlier. However the idea of efficiency in extracting information
was novel. [This entry was contributed by John Aldrich, based on David (1995).]
See also ASYMPTOTIC, ESTIMATION and PETERS’ METHOD.
The EHRENFEST (URN) MODEL was introduced in a paper
by Paul and
Tatyana Ehrenfest
"Über zwei bekannte Einwände gegen das Boltzmannsche H-Theorem," Physicalische
Zeitschrift, 8, (1907), 311-314 to show that the irreversibility
in Boltzmann’s thermodynamics did not contradict the recurrence properties of
dynamic systems. The Ehrenfest model was discussed from a mathematical
point of view by Mark Kac "Random Walk and the Theory
of Brownian Motion," American Mathematical Monthly, 54,
(1947), 369-391. It is treated as a Markov chain in the first edition
(1950) of W. Feller’s An Introduction to Probability Theory and
its Applications volume 1 while in the second (1957)
it first appears in a new section on urn models. [John Aldrich]
EIGENVALUE, EIGENFUNCTION, EIGENVECTOR and related terms. "Almost every combination
of the adjectives proper, latent, characteristic, eigen and secular, with the nouns root, number
and value, has been used in the literature for what we call a proper value" (P. R. Halmos Finite
Dimensional Vector Spaces (1958, 102)). To add to the confusion, both the values and their
reciprocals have been important: in A. Lichnerowicz’s Algèbre et analyse linéaires
(1947), valeur charactéristique and valeur propre are reciprocals of one another,
but the English (1967) translation has eigenvalue and proper value, which derive from
the same German word, Eigenwert. The adjectives also combine with other sorts of nouns,
including equations, solutions, functions and vectors. The story of the terminology ranges across
algebra, analysis and mechanics, classical and quantum physics.
Modern expositions of spectral theory often begin with a matrix A and introduce
value 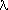 and vector x together in the value/vector-equation Ax =
and vector x together in the value/vector-equation Ax = 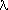 x :
any value
x :
any value 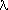 for which this equation is satisfied for a non-null x
is a value and the associated x is a vector. The existence of a non-null solution x
for (A -
for which this equation is satisfied for a non-null x
is a value and the associated x is a vector. The existence of a non-null solution x
for (A - 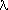 I)x = 0 requires the determinant of
(A -
I)x = 0 requires the determinant of
(A - 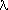 I) to be zero, i.e. that the roots of a polynomial
are significant. This finite-dimensional case is used to motivate the treatment of differential equations
and integral equations which involve infinite-dimensional spaces where the vector is now a function. The
historical order of development was more or less the reverse. The polynomial equation generated from the
differential equations of celestial mechanics came first, ca. 1780, then the equation was expressed using
determinants ca. 1830, then the equation was associated with matrices ca. 1880, then integral equations were
studied ca. 1900 until finally the modern order of topics starting from the value/vector-equation became established
ca. 1940. (Based on Kline ch. 29, 33, 45 & 46 and Hawkins (1975 and -7.))
I) to be zero, i.e. that the roots of a polynomial
are significant. This finite-dimensional case is used to motivate the treatment of differential equations
and integral equations which involve infinite-dimensional spaces where the vector is now a function. The
historical order of development was more or less the reverse. The polynomial equation generated from the
differential equations of celestial mechanics came first, ca. 1780, then the equation was expressed using
determinants ca. 1830, then the equation was associated with matrices ca. 1880, then integral equations were
studied ca. 1900 until finally the modern order of topics starting from the value/vector-equation became established
ca. 1940. (Based on Kline ch. 29, 33, 45 & 46 and Hawkins (1975 and -7.))
An early (but not the first) use of secular is
Jacobi’s famous paper in which
he introduced his eigenvalue algorithm.
The term secular (“continuing through long ages” OED) recalls
that one of the origins of spectral
theory was in the problem of the long-run behaviour of the solar system investigated by Laplace and Lagrange.
See Hawkins (1975). The 1829 paper in which Cauchy established that the roots of a symmetric determinant are
real has the title, "Sur l'équation à l'aide de laquelle on détermine les
inégalités séculaires des mouvements des planétes"; this signifed only that
Cauchy recognized that his problem, of choosing x to maximise xTAx
subject to xTx = 1 (to use modern notation), led to an equation like that studied in
celestial mechanics. Sylvester’s title "On the Equation to the Secular Inequalities in the Planetary Theory"
(see below) was even more misleading as to content. In this tradition the "Säkulärgleichung" of Courant
& Hilbert Methoden der Mathematischen Physik (1924) and the "secular equation" of E. T. Browne’s
"On the Separation Property of the Roots of the Secular Equation" American Journal of Mathematics, 52,
(1930), 843-850 refer to the characteristic equation of a symmetric matrix. The term "secular equation" appears
in the modern numerical linear algebra literature.
The characteristic terms derive from
Augustin Louis Cauchy
(1789-1857), who introduced the term l'equation caractéristique and investigated its roots in his
"Mémoire sur l'integration des équations linéaires,"
Exercises d'analyse et de physique mathématique, 1, 1840, 53 =
Oeuvres, (2),
11, 76 (Kline, page 801). Frobenius referred to this
memoir when he introduced the phrase "die charakteristische Determinante" in his fundamental paper on
matrices, "Über lineare Substitutionen und bilineare Formen," Jrnl. für die reine und angewandte
Math. (1874), 84, 1-63. In Les méthodes nouvelles de la mécanique céleste
(1892) Poincaré wrote about exposants (exponents) caractéristiques.
Sightings in JSTOR show the further expansion of the characteristic family and its spread
into English: characteristic value in G. D. Birkhoff, "Boundary Value and Expansion Problems
of Ordinary Linear Differential Equations," Trans. American Mathematical Society, 9,
(1908), 373-395, characteristic root in H. Hilton "Properties of Certain Homogeneous Linear
Substitutions," Annals of Mathematics, 2nd Ser., 15, (1913-1914) 195-201,
characteristic solution in W. D. A. Westfall "Existence of the Generalized Green’s Function"
Annals of Mathematics, 2nd Ser., 10, (1909), 177-180, characteristic vector
in J. W. Alexander "On the Class of a Covariant Tensor" Annals of Mathematics, 2nd Ser., 28,
(1926-1927), 245-250 and F. D. Murnaghan & A. Wintner "A Canonical Form for Real Matrices under
Orthogonal Transformations" Proceedings of the National Academy of Sciences of the United States
of America, 17, (1931), 417-420. C. C. MacDuffee’s standard work Theory of Matrices
(1933) used characteristic root, function and equation but found no use for
characteristic vector.
The latent terminology was introduced by
James Joseph Sylvester
(1814-1897) in the 1883 paper "On the Equation to the Secular Inequalities in the Planetary Theory"
Phil. Mag. 16, 267.
Coll Math Papers, IV, 110
It will be convenient to introduce here a notion (which plays
a conspicuous part in my new theory of multiple algebra), viz. that of the latent
roots of a matrix -- latent in a somewhat similar sense as vapour may be said
to be latent in water or smoke in a tobacco-leaf.
Sylvester’s "On the Three Laws of Motion in the World of Universal Algebra"
(Johns Hopkins University Circulars, 3, (1884)) contains the "law
of congruity ... which affirms that the latent roots of a matrix follow the
march of any functional operation formed on a matrix, not involving the action
of any foreign matrix."
Coll Math Papers, IV, 146. Sylvester also
used the term "latent equation" ("Lectures on the Principles
of Universal Algebra" American J. of Math. VI (1884), 216)
Coll Math Papers, IV, 208. "Latent vector" came later, perhaps as late as 1937
with A. C. Aitken’s "Studies in Practical Mathematics II. The Evaluation of the Latent Roots and Latent
Vectors of a Matrix," Proc. Royal Soc. Edinburgh, 57, 269-304. Previously H. Turnbull &
Aitken (Theory of Canonical Matrices, 1932) used the term "latent point" which they attributed to
Sylvester.
The eigen terms are associated with
David Hilbert
(1862-1943), though he may have been following such constructions
as Eigentöne in acoustics (cf. H. L. F. Helmholtz Lehre von den
tonempfindungen). Eigenfunktion and Eigenwert appear in the first
of Hilbert’s communications on integral equations “Grundzüge einer
allgemeinen Theorie der linearen Integralgleichungen”,
Nachrichten
von d. Königl. Ges. d. Wissensch. zu Göttingen (Math.-physik. Kl.) (1904) p. 49.-91. (The communications
from 1904-1910 were collected as Grundzüge
einer allgemeinen Theorie der linearen Integralgleichungen 1912). In
Whittaker & Watson’s Course of Modern
Analysis “Eigenfunktion” is translated as
“autofunction.” Eigenvektor appears in the exposition of the finite-dimensional case in Courant &
Hilbert Methoden der Mathematischen Physik (1924).
Hilbert’s original starting point was a non-homogeneous integral equation with a
parameter λ for which the matrix counterpart is (I - λA)x = y. Hilbert called the values of
λ that generate a non-null solution to
the homogeneous version of these equations Eigenwerte;
they are the reciprocals of the characteristic/latent roots of A. Courant & Hilbert (1924) uses κ
for a “characteristiche Zahl” and λ = (1/κ) for an “Eigenwert”;
Lichnerowicz (above) wrote the French equivalents. “Eigenwert” is
used in a different way in J. von Neumann’s “Allgemeine Eigenwerttheorie
Hermitescher Funktionaloperatoren”
Math.
Ann. 102 (1929) 49-131: “Ein Eigenwert ist eine Zahl, zu der
es eine Funktion f ≠ 0 mit Rf = λf ist dann Eigenfunktion.” This became the dominant
usage so that by 1946 H. & B. Jeffreys (Methods
of Mathematical Physics) were treating eigenvalue as synonymous with
characteristic value and latent root.
The development of MATRX MECHANICS in the 1920s promoted the use of the eigen terminology, for the new
theory was written in the language of Hilbert and his school. See chapter 3 of M.
Born, W. Heisenberg, and P. Jordan “Zur Quantenmechanik II,” Zeitschrift für Physik,
35, (1926), 557-615. [English translation
with commentary in B. L. van der Waerden, (editor) Sources of Quantum Mechanics (Dover Publications, 1968.)]
The passage of the eigen terms into English physics
can be followed through the OED and JSTOR. In 1926 P. A. M. Dirac
was writing “a set of independent solutions which may be called eigenfunctions”
(“On
the Theory of Quantum Mechanics”, Proc.
Royal Soc. A, 112, 661-677) (OED). Eigenvalue appears in a letter
to Nature (July 23, 1927) from A. S.
Eddington beginning “Among those ... trying to acquire a general
acquaintance with Schrödinger’s wave mechanics there must be many who find
their mathematical equipment insufficient to follow his first great problem—to
determine the eigenvalues and eigenfunctions for the hydrogen atom" (OED). Eigenvector appears in
R. Brauer & H. Weyl’s “Spinors in n Dimensions,” Amer. J. Math., 57, (1935) 425-449 (JSTOR).
While eigenvalue, eigenfunction and eigenvector were translations of German
originals, the eigenstate of
Dirac’s Principles of Quantum Mechanics (1930, p. 35) was a new construction and
it marks the arrival of eigen as a fully English particle. Eigenstate was
translated into German as Eigenzustand.
Proper has been a standard English rendering of "eigen" -- thus in the 19th century Helmholtz’s
Eigentöne became "proper tones." "Proper values" and "proper functions" appear in von Neumann’s
English writings, e.g. in his and S. Bochner’s "On Compact Solutions of Operational-Differential Equations. I,"
Annals of Mathematics, 2nd Ser., 36, (1935), 255-291 although "eigenvalue" is used in the
English translation (1949) of his Mathematische Grundlagen der Quantenmechanik (1932). Dirac
(Principles of Quantum Mechanics) argued against the proper terminology (and for the eigen) on the
ground that "proper" had other meanings in physics.
Paul Halmos (see above) followed von Neumann’s
English writings and used “proper value” in his widely-used
Finite Dimensional Vector Spaces (1958).
However Halmos admitted defeat in his A Hilbert Space Problem Book
(1967, p. x):
For many years I
have battled for proper values, and against the one and a half times translated
German-English hybrid that is often used to refer to them. I have now become
convinced that the war is over, and eigenvalues have won it; in this book I use
them.
The above information was contributed by John Aldrich.
In 2016, Jan Peter Schäfermeyer wrote:
Some time ago I researched the history of the power and related methods to
compute eigenvectors and found out that these methods were used first for
differential and integral equations, before they were used for the matrix
eigenvalue problem. Here
are the sources, mostly in German.
An interesting aside, that might be of interest for your webpage, concerns
the nomenclature of eigenvalues and eigenfunctions, terms that were
quickly adopted in the German literature after Hilbert had proposed them
in 1904. Before that, I haven't seen any particular names for these
entities. Schwarz simply speaks of a function w and a number c.
The French were more inventive: Picard in two papers,
Comptes Rendus 117 (1893),
and
C.R. 118 (1894),
speaks of
“points singuliers” and “valeurs singulieres,” but also has no particular
name for eigenfunctions:
Poincare proposes the names “nombres caracteristiques” and “fonctions
harmoniques” in an
1894 paper,
and in
1896
“fonctions fondamentales.”
And in the English literature I have found the terms “characteristic
numbers” and “characteristic functions” used by Bocher in his 1909
book on
integral equations.
EINSTEIN SUMMATION CONVENTION in TENSOR ANALYSIS. This
simplified way of writing tensor expressions was introduced by
Einstein in his great paper
on general relativity, “Die Grundlage der allgemeinen
Relativitätstheorie” Annalen der Physik, 49 (1916). “Later he said in jest
to a friend, ‘I have made a great discovery in mathematics; I have suppressed
the summation sign every time that the summation must be made over an index
which occurs twice..’” Abraham Pais ‘Subtle is the Lord...’: The Science and Life of Albert Einstein (1982, p. 216.)
ELEMENT in set theory. The
entry SET and SET THEORY describes how the German word Menge used by Cantor came to be
translated as set. The history of the companion word element is
much simpler for the term was adopted from an early date and it is essentially
the same in German, French and English: Element, élément and element.
Cantor first used the German word Element in his “Ueber
unendliche, lineare Punktmannichfaltigkeiten,”
Mathematische Annalen
(1882) XX p. 114.
The French word élément appeared in his “Une contribution á
la théorie des ensembles,” Acta Mathematica, 2, (1883), p. 311.
The English word appears in Bertrand Russell’s Principles of Mathematics (1903).
Element was not a new word:
derivatives of the Latin word elementum had been in English, French and
German for centuries and had been used in various mathematical contexts. Thus Euclid’s
work was translated into English in 1570 as The Elements of Geometry while in
1867 C. L. Dodgson was referring to the elements of a block (i.e.
a MATRIX). In German von Staudt used the term Elemente
(elements) in his Geometrie der Lage (2nd ed., 1856): “Wenn man die
Menge aller in einem und demselben reellen einfoermigen Gebilde enthaltenen
reellen Elemente durch n + 1 bezeichnet und mit diesem Ausdrucke, welcher
dieselbe Bedeutung auch in den acht folgenden Nummern hat, wie mit einer endlichen
Zahl verfaehrt, so ... ”
[John Aldrich and Ken Pledger contributed to this entry.]
The term ELEMENTARY DIVISOR was first used in German by
Weierstrass, according to Maxime Bôcher in Introduction to
Higher Algebra.
Elementary divisor is found in English in April 1893 in
“On
the Determination of Groups Whose Order is a Power of a Prime” by
J. W. A. Young in American Journal of Mathematics
Vol. 15, No. 2, pp. 124-178. [Google print search by James A. Landau]
ELEMENTARY OPERATIONS (TRANSFORMATIONS) on (of) a matrix. According to Wedderburn
Lectures on Matrices (1934, p. 169) “the notion of an elementary transformation seems to be due in
the main” to Grassmann Ausdehnungslehre 1862.
Elementary transformations of a matrix are defined by M. Bôcher Introduction to Higher Algebra (1909, p.
55). More recently the term elementary operation has been preferred. For an
early instance see W.J. Duncan, R.A. Fraser, A. R. Collar Elementary Matrices and Some Applications to Dynamics
and Differential Equations (1938).
ELIMINANT. According to George Salmon in Modern Higher
Algebra (1885), “The name ‘eliminant’ was introduced I think by
Professor De Morgan. ... The older name ‘resultant’ was employed by
Bezout, Histoire de l'Académie de Paris, 1764.”
Eliminant is found in 1859 in
“Lessons
introductory to the Modern Higher Algebra”
by George Salmon.
Page 18 has “The result of eliminating n variables between n homogeneous equations of any degree is called the eliminant of these equations.”
Eliminant is found in 1881 in
The Theory of Equations: With an Introduction to the Theory of Binary Algebraic Forms
by William Snow Burnside and Arthur William Panton:
"Being given a system of n equations,
homogeneous between n variables, or non-homogeneous
between n - 1 variables, if we combine
these equations in such a manner as to eliminate the variables,
and obtain an equation R = 0, containing
only the coefficients of the equations; the quantity R is, when expressed in a rational and integral form, called
their Resultant or Eliminant." [Google print search by James A. Landau]
ELIMINATE is found in English in 1818 in Elements
of Algebra
by S. F. Lacroix, Translated from the French
For the use of the students of the University at Cambridge, New England.
[Google print search by James A. Landau]
ELIMINATION is found in 1764 in Bézout’s
“Recherches sur le degré des Équations résultantes de l'évanouissement des
inconnues, & sur les moyens qu'il convient d'employer pour trouver ces Équations,”
Histoire de l'Académie royale des sciences Ann. 1764.
Elimination is found in English in 1801 in a review of
La Croix’s Elémens d’Algèbre in The Monthly Review; or Literary Journal.
[Google print search by James A. Landau].
ELLIPSE was probably coined by Apollonius, who, according to
Pappus, had terms for all three conic sections. Michael N. Fried says
there are two known occasions where Archimedes used the terms
"parabola" and "ellipse," but that "these are, most likely, later
interpolations rather than Archimedes own terminology."
James A. Landau writes that the curve we call the "ellipse" was
generally called an ellipsis in the seventeenth century,
although the word Elleipse appears in a letter written by
Robert Hooke in 1679. Ellipse appears in a letter written by
Gilbert Clerke in 1687.
ELLIPSOID. According to the 1900 translation by Beman and Smith of
Geschichte der Elementar-Mathematik by Karl Fink:
"Instead of Euler’s names: 'elliptoid, elliptic-hyperbolic,
hyperbolic-hyerbolic, elliptic-parabolic, parabolic-hyperbolic
surface,' the terms now in use, 'ellipsoid, hyperboloid, paraboloid,'
were naturalized by Biot and Lacroix."
Ellipsoid appears in a letter written in 1672 by Sir Isaac
Newton [James A. Landau].
ELLIPTIC CURVE. In 1901 “A Problem
and its Solutions” by Euplio Conoscente in Proceedings of the London Mathematical Society
has: “It ought to be so for the coordinates of an elliptic curve are expressed by elliptic functions of the Abelian integral of the first kind relative to its equation.” [Google print search by James A. Landau]
In 1908, volume three of
Lehrbuch
der Algebra by Heinrich Weber has an initial section called "Die
elliptische Integrale" with subsection 6 called "Elliptische Kurven."
That subsection includes this statement:
Wir wollen hier alle Kurven, deren Differentiale und Integrale
auf elliptische reduzierbar sind, e l l i p t i s c h e K u r v e n nennen.
... Wir werden sehen, dass alle Kurven dritten grades ohne Doppel- oder Rueckkehrpunkt
zu den elliptischen gehoeren. Kurven hoeheren Grades koennen nur dann dazu gehoeren,
wenn sie eine gewisse Anzahl singulaerer Punckte haben.
[This citation was provided by William C. Waterhouse.]
Elliptic curve is found in Webster’s New International
Dictionary (1909), defined as “one of the genus 1.”
ELLIPTIC FUNCTION has had two meanings: 1) what we now call an
“elliptic integral” 2) the doubly periodic functions which are the inverse of
the elliptic integral.
Fonction elliptique was used with meaning 1) by Legendre
in his 1792 paper “Mémoire Sur Les Transcendantes Elliptiques.”
Elliptic function appeared
in English in 1809 in the translation of this paper in Thomas Leybourn, ed The
Mathematical Repository, New Series, Volume III (1809).
Fonctions elliptiques with meaning 2) appeared in
a letter by Jacobi, “Suite des notices sur les fonctions elliptiques,” which was published in volume III (1828) of Crelle.
In 1844 elliptic function appears in the title
A Treatise on the Integral calculus, containing the Integration of Explicit Functions of One Variable; Together With The Theory of Definite Integrals and of Elliptic Functions
by J. Hymers, DD.
In 1847 in Report
of the Sixteenth Meeting of the British Association for the Advancement of
Science in the article “On the Recent Progress of
Analysis (Theory of the Comparison of Transcendentals)” by R. L. Ellis
writes, “Following M. Jacobi, we shall henceforth give the name of
elliptic functions to those which are analogous to circular functions. It is
on this account better to call Legendre’s functions elliptic integrals than, as
he has done, elliptic functions.”
[This entry was contributed by James A. Landau.]
ELLIPTIC GEOMETRY. See HYPERBOLIC GEOMETRY.
ELLIPTIC INTEGRAL. According to the DSB, "Giulio Carlo Fagnano
dei Toschi (1682-1766) gave the name 'elliptic integrals' to
integrals of the form int f(x1 sqrt P[x]) dx where P(x) is
a polynomial of the third or fourth degree."
According to Elliptic Functions and Elliptic Integrals by
V. Prasolov and Y. Solovyev, AMS, 1997 (Translations of Mathematical
Monographs, v. 170):
The most remarkable properties of the lemniscate were discovered by
an Italian mathematician Count Fagnano (1682-1766). By the way, it
was Fagnano who coined the term elliptic integrals. Fagnano
discovered that the arc length of the lemniscate can be expressed in
terms of an elliptic integral of the first kind. He obtained an
addition theorem for this integral and, therefore, demonstrated that
the division of arcs of the lemniscate into n equal parts is an
algebraic problem.
[From a post in sci.math by David Cantrell]
EM ALGORITHM. The term and the method were introduced by
A. P. Dempster; N. M. Laird & D. B. Rubin "Maximum Likelihood from
Incomplete Data via the EM Algorithm," Journal of the Royal Statistical Society,
B, 39, (1977), 1-38. "This paper presents a genereal approach to
iterative computation of maximum-likelihood estimates when the observations
can be viewed as incomplete data. Since each iteration of the algorithm consists
of an expectation step followed by a maximization step we call it the EM algorithm."
The paper gives many references to related earlier work, the oldest to a paper
from 1926 by A. G. McKendrick.
(David (2001)).
EMPTY SET. A JSTOR search found the term used--without explanation--in J. E.
McAtee "Modular Invariants of a Quadratic Form for a Prime Power Modulus," American
Journal of Mathematics, 41, (1919), p. 237. The term began to become common in the
1930s, although in these early days it was nothing like as common as null set.
ENDOGENOUS/EXOGENOUS VARIABLE. In the SIMULTANEOUS EQUATIONS MODEL
of ECONOMETRICS variables are either endogenous or exogenous. The terms were coined around 1945
by Tjalling C. Koopmans. He explained them as follows, "[Exogenous variables] are
variables that influence the endogenous variables but are not themselves
influenced by the endogenous variables". [The] exogenous variables are treated
as if they are given functions of time, the values of which remain the same in
repeated samples." p. 56 of Koopmans & H. Rubin "Measuring the Equation
Systems of Dynamic Economics," chapter II of Koopmans (ed.) Statistical Inference in
Dynamic Economic Models (1950). The terms endogenous and exogenous were taken from business cycle
theory. In his work on the simultaneous equations model Haavelmo had used the
terms "dependent" and "autonomous." The Probability Approach in Econometrics," Econometrica, 12, Supplement. (1944), pp. 86-7.
In econometrics the term
exogenous variable is often used where in other branches of statistics
independent variable or regressor or covariate might be used.
See DEPENDENT/INDEPENDENT VARIABLE, REGRESSION,
COVARIATE.
ENTROPY. The concept originated in thermodynamics, was extended by analogy to information theory
and then by analogy again to dynamical systems.
The concept was introduced into physics by
Rudolf Clausius (1822-1888)
"Ueber verschiedene für die Anwendung bequeme Formen
der Hauptgleichungen der mechanischen Wärmetheorie," Annalen
der Physik und Chemie, 125, (1865) 353. Clausius gave a full account of how he chose the
name:
If we wish to designate S by a proper name we can say
of it that it is the transformation content of the body, in the same
way that we say of the quantity U that it is the heat and work content
of the body. However, since I think it is better to take the names of such quantities
as these, which are important for science, from the ancient languages, so that
they can be introduced without change into all the modern languages, I proposed
to name the magnitude S the entropy of the body, from the Greek
word 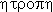 , a transformation. I have
intentionally formed the word entropy so as to be as similar as possible
to the word energy, since both these quantities, which are to be known
by these names, are so nearly related to each other in their physical significance
that a certain similarity in their names seemed to me advantageous.
, a transformation. I have
intentionally formed the word entropy so as to be as similar as possible
to the word energy, since both these quantities, which are to be known
by these names, are so nearly related to each other in their physical significance
that a certain similarity in their names seemed to me advantageous.
Ludwig Boltzmann
(1844-1906) gave a probabilistic interpretation of entropy and expressed entropy in terms of the integral of
f log f in "Weitere Studien über
das Wärmegleichgewicht unter Gasmolekülen" Sitzungsberichte.
Akad. Wiss. Wien, part II, 66, (1872), 275-370. There is an English
translation in S. G. Brush, Kinetic Theory, Vol. II, pp. 88-175, (1965).
In A Mathematical Theory of Communication
(1948, p.11) C. E. Shannon (1916-2001)
set down a "reasonable" set of requirements for a measure of information and showed that
the only expression satisfying them has a form that "will be recognized as that
of entropy as defined in certain formulations of statistical mechanics." So
he called the measure "entropy." See INFORMATION THEORY.
A. N. Kolmogorov
applied information theory to the ergodic theory of dynamical systems in "On the Entropy per Time Unit
as a Metric Invariant of Automorphisms," Doklady akademi nauk, 124,
(1959), 754-5.
An article by J. Willard Gibbs, “Graphical Methods in the
Thermodynamics of Fluids” has a footnote: “The term entropy, it will be observed, is here
used in accordance with the original suggestion of Clausius, and not in
the sense in which it has been employed by Professor Tait and others
after his suggestion. The same quantity has been called by Professor
Rankine the Thermodynamic function. ...”
This entry was contributed by John Aldrich, with the footnote added by James A. Landau.
ENTSCHEIDUNGSPROBLEM. See DECISION PROBLEM.
The term EPICYCLE was used in the
astronomical system of Claudius Ptolemy
to signify a small circle, having its centre
on the circumference of a bigger circle. The English word came via Latin from
the Greek 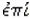 upon +
upon + 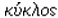 circle. The earliest
quotation in the OED is from Chaucer’s Treatise on the Astrolabe (about 1391): “The Moone Moeuyth the contrarie from othere planetes as in hire
Episicle.”
circle. The earliest
quotation in the OED is from Chaucer’s Treatise on the Astrolabe (about 1391): “The Moone Moeuyth the contrarie from othere planetes as in hire
Episicle.”
The term EPICYCLOID was used by Philippe de La Hire in
Traité des épicycloïdes et leur usage en mécanique, which he read to the
Academy of Sciences in 1694. A footnote in the Collected Works of Jacob Bernoulli
says the term is apparently due to La Hire. [Information provided by François Ziegler.]
Epicycloid is found in English in 1695 in
“The
Quadrature of a Portion of the Epicycloid” by a Mr. Caswel or Caswell (both spellings appear) in Philosophical Transactions For the Month of October, 1695.
[Google print search by James A. Landau]
EPIMOMORPHISM. See the entry MONOMORPHISM.
EPONYMY and LAWS OF EPONYMY. Names in
mathematics often make reference to a person. These pages contain hundreds of
examples, from ABELIAN EQUATION to ZORN’S LEMMA, or,
in time, from the PYTHAGOREAN THEOREM to
GRAHAM’S NUMBER. There is no uniform relation
between "thing" and person: ZORN’S LEMMA is a name that contemporaries of Zorn gave to
a proposition that can be found (more or less) in a work by him;
CARTESIAN PRODUCT arrived
nearly 300 years after Descartes in a branch of mathematics that did not exist
in his time and there was never any question of looking it up in his work.
Instances of eponymy prompt obvious questions, e.g. of BAYES
it has been asked, "Who discovered Bayes’s theorem?" and "Was Bayes a
Bayesian?" Sometimes a ‘wrong’ answer inspires an attempt to alter usage:
see MACLAURIN’s SERIES for an unsuccessful effort and
GAUSS-MARKOV THEOREM for a half-successful one. The story of another half-successful
attempt, the RAO-BLACKWELL THEOREM, throws some light on what makes an
eponym successful. Sometimes an incorrect attribution just stands with no
attempt to change it, e.g. VANDEMONDE DETERMINANT.
The general practice of eponymy has attracted attention, especially
the widespread phenomenon of misattribution. Stigler (see below) quotes
a cynical remark from an unnamed historian of science,
"Every scientific discovery is named
after the last individual too ungenerous to give due credit to his predecessors."
Misattribution has also inspired laws of eponymy--eponymous
laws of eponymy, naturally.
Boyer’s law, that "mathematical
formulas and theorems are usually not named after their original discoverers,"
was proposed by H. C. Kennedy ("Who Discovered Boyer’s Law?" Amer. Math.
Monthly, 79:1 (1972), 66-67) on the basis of the many instances described
in Carl B. Boyer’s History of Mathematics (1968). Boyer gave his opinion
of eponymy in the exclamation, "Clio, the muse of history, often is fickle in
attaching names to theorems!"
Stigler’s law of eponymy, that "no scientific discovery is ever named after its original
discoverer," was formulated by Stephen Stigler ("Stigler’s Law of
Eponymy" (1980), reprinted in Stigler (1999)). Unlike Boyer, Stigler saw
patterns in naming and attempted to explain them using the ideas of the
sociologist Robert K.
Merton. Stigler tried out his hypotheses in a case study of the
GAUSSIAN (NORMAL) distribution.
Another law complicating eponymy is Whitehead’s law: "Everything of
importance has been said before by someone who did not discover it." (The remark
was popularised by Merton but
Michael Berry
calls it a law.) See the entry RAO-BLACKWELL
for an illustration of the difficulty of applying this law, especially to the
work of a living discoverer who argues back.
Whitehead’s remark is from
the essay Organisation of Thought published in a collection with the same title (1917). He was discussing the
relation between traditional logic and modern logic and the sentence before
read, "To come near to a true theory and to grasp its precise application
are two very different things, as the history of science teaches."
Berry, incidentally, calls the Boyer-Stigler law Arnold’s law after
V. I. Arnol’d
who complains of Western neglect of Russian
contributions: see the entry CAUCHY-SCHWARZ for an instance.
[This entry was contributed by John Aldrich.]
EQUAL (in area and volume). In 1832 Elements of Geometry
and Trigonometry by David Brewster (which is a translation of
Legendre) has:
It is customary with Euclid, and various geometrical
writers, to give the name equal triangles, to triangles which
are equal only in surface; and of equal solids, to solids
which are equal only in solidity. We have thought it more suitable
to call such triangles or solids equivalent; reserving the
denomination equal triangles, or solids, for such as
coincide when applied to each other.
EQUATION. Diophantus used the words isotas and isosis in his Arithmetica.
This was translated ca. 860 CE by Qusta ibn Luqa with the Arabic word 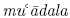 .
The Arabic term was used by many later algebraists in the Islamic world. The Latin equatio is probably a translation from the Arabic.
[Jeffrey A. Oaks]
.
The Arabic term was used by many later algebraists in the Islamic world. The Latin equatio is probably a translation from the Arabic.
[Jeffrey A. Oaks]
Equatio appears in the ordinary high school sense of the word
in Fibonacci’s Liber Abbaci, Ch. 15, section 3
[Barnabas Hughes].
Equatio was used by Medieval writers.
Ramus used aequatio in his arithmetic (1567).
Equation appears in English in 1570 in Sir Henry Billingsley’s
translation of Euclid’s Elements: "Many rules...of Algebra,
with the equations therein vsed." It also appears in the preface to
the translation, by John Dee: "That great Arithmeticall Arte of
Aequation: commonly called...Algebra."
Viete defines the term equation in chapter 8 of In artem
analyticem isagoge (1591), according to the DSB.
EQUIANGULAR. Equiangle appears in English in 1570 in
Sir Henry Billingsley’s translation of Euclid: "To describe a
triangle equiangle vnto a triangle geuen" (OED2).
Equiangular is found in English in 1660 in Barrow,
Euclid: "An Equiangular or equal-angled figure is that whereof
all the angles are equal" (OED2).
Isogon (or isagon) is found in a 1696 dictionary.
EQUILATERAL. Equilateral triangle is found in English
in 1570 in Sir Henry Billingsley’s translation of Euclid: "How to describe
an equilaterall triangle redily and mechanically" (OED). Billingsley simply anglicised the
Latin term.
A few years before (in 1551) Robert
Recorde had proposed an English expression in his Pathway to
Knowledge: "That the Greekes doo call Isopleuron, and Latine men aequilaterum: and in english it may be
called a threlike triangle" Recorde’s English terms (there was a family of
them) did not take root as he acknowledged in his last work. In this—it is
written in the form of a dialogue—the “Master” states, “if I should give them [mathematical
terms] newe names, many would make a quarrelle against, for obscuring the old
Arte with newe names; as some all redy have done.” In German local terms did take root and gleichseitig
(equal-sided) became the standard term. (Based
on G. Howson A History of Mathematics Education in England 1982.)
See also the entry ISOSCELES.
EQUIPROBABLE. In 1853 a review of the book Essays on Life
Assurance by Edward Sang has: “Now Mr. Sang ought to have
known, not merely that M. Legendre did not attempt to demonstrate the
method of minimum squares, but that Gauss and La Place did attempt to do
so, the former aided by the consideration of equi-probable errors, and
the latter, with complete success, by that of equi-possible
combinations.” The review is found in
The
Assurance Magazine, and Journal of the Institute of Actuaries. [Google print search by James A. Landau]
EQUIVALENT (MATRIX) was introduced by K. Hensel (as “ähnlich”) in
“Ueber lineare Substitutionen und bilineare Formen,”
J.
reine angew. Math. Vol. 84 (1879) p. 21. This is according to C. C. MacDuffee,
The Theory of Matrices, Springer (1933).
Equivalent is found in 1884
in an article in The Messenger of Mathematics. [Google print search by James A. Landau]
ERGODIC. Ludwig Boltzmann (1844-1906) coined the term Ergode (from the Greek words for work
+ way) for what Gibbs later called a "micro-canonical ensemble"; Ergode appears in the 1884 article
in Wien. Ber. 90, 231. Later P. & T. Ehrenfest (1911) "Begriffiche Grundlagen der
statistischen Auffassung in der Mechanik" (Encyklopädie der mathematischen Wissenschaften,
vol. 4, Part 32) discussed "ergodische mechanischer Systeme" the existence of which they saw as underlying
the gas theory of Boltzmann and Maxwell. (Based on a note on p. 297 of Lectures on Gas Theory,
S. G. Brush’s translation of Boltzmann’s Vorlesungen über Gastheorie.)
After the impossibility of an ergodic mechanical system was demonstrated, various related hypotheses
were investigated. "Ergodic" and "quasi-ergodic" theorems were proved in the 1930s, by, amongst others,
G. D. Birkhoff in Proc. Nat. Acad. Sci. (1931) 17, 651 -- "I propose ... to establish a general
recurrence theorem and thence the 'ergodic theorem'" -- and J. von Neumann Proc. Nat. Acad. Sci.
(1932) 18, 70-82.
Ergodic theorems originated in classical mechanics but in the theory of stochastic processes
they appear as versions of the law of large numbers, see e.g. J. L. Doob’s Stochastic Processes (1954).
[This entry was contributed by John Aldrich.]
ERLANGEN PROGRAM (in German, Erlanger Programm.) In 1872 the 24 year-old
Felix Klein
became a professor at the University of Erlangen and "by tradition
he was required to circulate a written programme of work plans." Grattan-Guinness
(p. 547) Klein’s program was entitled "Vergleichende Betrachtungen über
neuere geometrische Forschungen" (A Comparative Review of Recent Researches
in Geometry.) The paper was widely translated and Klein reissued it in
Mathematische
Annalen, 43, (1893),63-100.
The phrase "Erlangen program" has referred variously to the
paper, to the injunction which it contains,
"Given a manifold and a group of transformations of the manifold, to study
the manifold configurations with respect to those features which are not altered
by the transformations of the group." (p. 67, translated in Roberto Torretti
Nineteenth
Century Geometry), to the work that followed the injunction and
to the underlying interpretation of geometry. [John Aldrich]
ERROR, LAW OF ERROR, THEORY OF ERRORS, etc. Between
1750 and 1830 mathematicians and astronomers (who were usually the same people)
created the first elaborate theory of statistical inference, the theory of
errors. In the 20th century the theory was
extended to new areas including regression and the analysis of variance.
Many special terms were introduced in the 19th
century as the theory was expounded and consolidated. In
the 20th century more new terms appeared and some of the old ones
were retired.
Thomas Simpson’s On
the Advantage of Taking the Mean of a Number of Observations
(1755) was an early attempt to subject to probabilistic analysis the "method
practiced by Astronomers" of taking the mean of several observations "in order
to diminish the errors arising from the imperfections of instruments and the
organs of sense." By the early 19th century some far reaching theory
had been developed with Gauss and Laplace the leading contributors. See CENTRAL LIMIT THEOREM
and METHOD OF LEAST SQUARES
Astronomers recognised different kinds of errors, e.g. W. Chauvenet
A Manual of Spherical and Practical Astronomy ... with
an Appendix on the Method of Least Squares (4th edition,
1871, p. 470) distinguished between irregular and constant errors, subdividing
the latter into 3 categories. The theory of errors was about eliminating the
effects of irregular errors.
Error was associated not only with the individual observations
but with the inferences based upon them. Thus the title of Gauss’s Theoria
combinationis observationum erroribus minimis obnoxiae (1821/3) translates
as the Theory of the combination of observations least subject to error and
the main business of this work was to show that the method of least squares
produces the required combination. The 20th century terms sampling
error (see Fisher
Statistical
Methods for Research Workers (1925, §26))
and Type I error are concerned with errors of inference in estimation
or testing and have no necessary connection with errors of observation. See
the entries GAUSS-MARKOV THEOREM
and TYPE I ERROR.
Bessel’s probable error (wahrscheinliche Fehler)
was a measure of (un)reliability that could apply both to an individual observation
and to a combination of observations like the mean. Today there are two distinct
terms, the standard deviation and the standard error. For details see the entries
PROBABLE ERROR, STANDARD ERROR
and STANDARD DEVIATION.
Law of error A. De Morgan Essay on Probabilities (1838) asked, "what do we mean by a law of error?"
and went on to describe "the standard law
of facility of error" (p. 143). This law had been used by Gauss in his first (1809) theory
of least squares and is called the normal or Gaussian distribution today. There
were many variations on the De Morgan terminology but the boldest and
simplest was the law of error. There is a chapter on the law in W. S.
Jevons’s Principles of Science (1874). See the entries NORMAL
and GAUSSIAN and also Symbols Associated with the Normal Distribution on the
Symbols
in Probability and Statistics page.
Theory of errors. According to Sheynin Theory of
Probability: A Historical Essay p. 57, the
term “theory of errors” was not used by Gauss or Laplace and is due to Bessel
who first used it in 1820 in his “Beschreibung des auf
des Königsberger Sternwarte,” Astron. Jahrb. (Berlin) für 1823, 161–168. The English expression appears in
the title of G. B Airy’s 1861 book, On the
Algebraical and Numerical Theory of Errors of Observation and the Combination
of Observations. This title contains another popular name for the
subject, viz. the combination of observations.
Error function. In the course of the19th century the function from the
theory of errors appeared in several contexts unrelated to probability, e.g.
refraction and heat conduction. In 1871 J. W. Glaisher wrote that "Erf x
may fairly claim at present to rank in importance next to the trigonometrical
and logarithmic functions." Glaisher introduced the symbol Erf and the name
error function for a particular form of the law as follows:
As it is necessary that the function should have a name, and as I do not know
that any has been suggested, I propose to call it the Error-function
... and to write

("On a Class of Definite Integrals, Philosophical Magazine, 42,
1871, p. 296) Glaisher also introduced the error-function-complement with
the symbol Erfc. The names and symbols continue to be used though often the
definitions are slightly different from Glaisher’s.
When R. A. Fisher wrote about regression and
the analysis of variance he was reviving the theory of errors. He and his followers
reinterpreted old terms and produced new ones. They considered their extensions
so radical that they were no longer working in the theory of errors; that was
now part of history: see Fisher’s
Statistical
Methods for Research Workers (1925, §1).
Experimental error. In
"The
Arrangement of Field Experiments",
Journal of the Ministry of Agriculture of Great Britain, 33, (1926),
503-513 Fisher extended the notion of error when he explained
that "experiments of the uniformity trial type have demonstrated the magnitude
and ubiquity of that class of error which cannot be ascribed to carelessness
in measuring the land or weighing the produce, and which is consequently described
as due to ’soil heterogeneity.'" In the analysis of variance Fisher had
a category "variance due to experimental error": see
Statistical
Methods for Research Workers (1925, §48, Table 58). See the entry
VARIANCE.
Error term. In his formulation of REGRESSION Fisher
wrote the regression equation as a relation between the mean value of the
dependent variable and the values of the independent variables: see
Statistical Methods for
Research Workers (1925, §26). In the econometric literature the equations of the
SIMULTANEOUS EQUATIONS MODEL were written with "random shifts" as in T. Haavelmo
"The Probability Approach in Econometrics," Econometrica, 12, Supplement. (1944), p. 99 or
with "disturbances" as in Koopmans & H. Rubin "Measuring the Equation
Systems of Dynamic Economics" p. 59. However these expressions were soon displaced
by "error." The expression error term appears in the title of D. Cochrane & G. H. Orcutt’s
"Application of Least Squares Regression to Relationships Containing Auto-Correlated Error
Terms," Journal of the American Statistical Association, 44,
(1949), 32-61.
Fisher’s regression was given a new look by J. Durbin and G. S. Watson
("Testing for Serial Correlation in Least Squares
Regression: I," Biometrika, 37, (1950), p. 410) when they wrote

in "which y the dependent variable and x, the
dependent variable, are observed, the errors ε being unobserved."
They (p. 411) also gave the matrix version
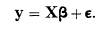
Although the error formulation of the regression
equation was introduced by writers on time series analysis/econometrics, who
were used to including random shocks or disturbances in their models, the
formulation was equally natural in experiments and the analysis of variance and
was adopted in such works as O. Kempthorne’s Design
and Analysis of Experiments (1952) and H. Scheffé’s Analysis of Variance (1959). See the
entries REGRESSION, RESIDUAL and VARIANCE.
Errors in variables and errors in equations. These expressions came into use
around 1950 to indicate two ways of modelling the relationship between
variables. They appear, for instance, in M. G. Kendall’s "Regression,
Structure and Functional Relationship Part I," Biometrika, 38, (1951), p. 11.
The errors in equation formulation figures in the
Fisher regression model and in the SIMULTANEOUS EQUATIONS MODEL
and has just been described under the heading error term. In the errors in variables
formulation there is an exact relationship between unobserved true values of the variables but the
observations are contaminated by measurement error. Interest in this
formulation went back to the late 19th century. D. V. Lindley began
his literature review with the work of C. H. Kummel (1879) in his paper "Regression Lines and the
Linear Functional Relationship," Supplement
to the Journal of the Royal Statistical Society, 9, (1947), 218-244.
This entry was contributed by John Aldrich.
ESCRIBED CIRCLE is found in 1847 in
The Solutions of the Geometrical Problems: Consisting Chiefly of Examples in Plane Co-ordinate Geometry
by Thomas Gaskin: "The lines joining the angles of a triangle with the points in which the escribed circles
touch the opposite sides, meet in a point. Shew also that if the base and
the sum of the other sides is constant, the locus of the centre of the
escribed circle touching the base is an ellipse." [Google print search]
ESTIMATION. Long before the terminology stabilized around estimation the activity was called calculation,
determination or fitting.
The terms estimation and estimate were introduced
in R. A. Fisher’s "
On the Mathematical Foundations of Theoretical Statistics.
" (Phil. Trans. R. Soc. 1922). He writes (none too helpfully!):
"Problems of estimation are those in which it is required to estimate the
value of one or more of the population parameters from a random sample of the
population." (p. 310) Fisher uses estimate
as a substantive sparingly in the paper. The same paper introduced three criteria
of estimation: consistency, efficiency and sufficiency.
The phrase unbiassed estimate appears in Fisher’s
Statistical
Methods for Research Workers (1925, p. 54) although the idea is much older.
The expression best linear unbiased estimate appears in 1938 in F. N. David and J. Neyman,
"Extension of the Markoff Theorem on Least Squares," Statistical
Research Memoirs, 2, 105-116 (see entry on Gauss-Markov theorem). In his
"On the Two Different Aspects of the Representative Method" (Journal
of the Royal Statistical Society, 97, (1934), 558-625) Neyman had used mathematical
expectation estimate for unbiased estimate and best linear estimate
for best linear unbiased estimate.
Following Neyman’s (ibid.) introduction of confidence intervals (q.v.) the expression interval
estimation came into use. It appears in E. S. Pearson
"Some Aspects of the Problem of Randomization" Biometrika, 29, (1937), pp. 53-64, though
Neyman himself (Phil. Trans. R. Soc. A 236, (1937), p. 346) wrote of
"estimation by unique estimate" and "estimation by interval". Point
estimation and interval estimation are used as contrasting terms in
Henry Scheffé "Statistical Inference in the Non-Parametric Case"
Annals of Mathematical Statistics, 14, (1943), pp. 305-332.
The term estimator was introduced in 1939 in E. J. G. Pitman, "The Estimation of the Location
and Scale Parameters of a Continuous Population of any Given Form," Biometrika,
30, 391-421. Pitman (pp. 398 & 403) used the term in a specialised sense:
his estimators are estimators of location and scale with natural invariance
properties. Now estimator is used in a much wider sense.
This entry was contributed by John Aldrich. See also CONFIDENCE INTERVAL, CRAMÉR-RAO INEQUALITY,
CRITERIA OF ESTIMATION, DECISION THEORY, GAUSS-MARKOV THEOREM, MAXIMUM LIKELIHOOD, METHOD OF LEAST SQUARES,
MINIMUM χ2, RAO-BLACKWELL THOREM, STANDARD ERROR.
ETHNOMATHEMATICS. In a 1959 Italian paper, “Per una maggiore attenzione all’etnologia matematica,” Rivista di Antropologia, O. Falsirol,
appraising the work of Ewald Fettweis, wrote:
Professore all’Accademia Pedagogica di Aachen, dove
tenne lezioni di didattica, di storia delle matematiche e
di etnomatematica fino al 1954, egli dedicò e viene
dedicando parte considerevole della sua attività scientifica
alla matematica e all’astronomia dei popoli
considetti primitivi.
[Professor at the Paedagogische Akademie in Aachen,
he lectured on mathematical education, history of
mathematics, and ethnomathematics until 1954. He
focused his research on the study of the mathematics
and astronomy of primitive people.]
This information, including the English translation, is taken from “Ethnomathematics in the 1930s —
The Contribution of Ewald Fettweis to the History of Ethnomathematics,” by Andrea V. Rohrer and Gert Schubring,
For the Learning of Mathematics 31, 2 (July, 2011). The article states that the term first appeared in print in 1959.
In 1997 Ubiratan D'Ambrosio stated that he had coined the term, writing the following to Julio González
Cabillón (who provided the translation from Spanish to
English):
In 1977, the AAAS hosted a conference on Native American
Sciences, where I presented a paper about "Science in Native
Cultures," and where I called attention to the need for extending the
methodology of Botany (ethnobotany was already in use) to the
scientific knowledge as a whole, and to mathematics, doing "something
like ethnoscience and ethnomathematics." That paper was never
published. Five years later, in a meeting in Suriname in 1982, the
concept was mentioned more explicitly. In the following years, I began
using ethnomathematics. But it was not until ICME 5 that the
term was "officially" recognized. My book Socio-cultural Bases for
Mathematics Education brings the first study about
Ethnomathematics.
In the above, ICME 5 refers to the Fifth International Congress on
Mathematics Education, held in Adelaide, Australia, in August 1984.
The AAAS is the American Association for the Advancement of Science,
of which Ubiratan D'Ambrosio is a Fellow.
EUCLIDEAN was used in English in 1660 by Isaac Barrow
(1630-1677) in the preface of an edition of the Elements
(OED2).
EUCLIDEAN ALGORITHM. Gauss used the term continued fraction algorithm.
Der Euclidische Algorithmus is found in 1902 in
Nidere Zahlentheorie. Erster Teil
by Dr. Paul Bachmann.
Euclidean algorithm is found in Englsih in July 1903 in a review
of the above book in the Bulletin of the American Mathematical Society.
[Google print searches by James A. Landau.]
EUCLIDEAN GEOMETRY is found in English in 1723 in the title
A System
of the Mathematics, Containing The Euclidean Geometry, Plane and Spherical Trigonometry, the Projection of the Sphere, both Orthographic and Stereographic, Astronomy, the Use of the globes and Navigation
by James Hodgson. [Google print search by James A. Landau]
EULER. Leonhard
Euler (1707-83) is generally considered the most prolific mathematician
of all time. Karl Pearson wrote, "It does not matter what field you take up
in pure or applied mathematics you will find Euler’s name attached to one or
more theorems, or one or more theorems to which it ought to be attached." Lectures
on the History of Statistics in the 17th and 18th Centuries (p. 245).
Besides theorems, there are Euler conjectures, diagrams, equations, formulas,
etc. The terms appear in analysis, topology, number theory, combinatorics, mechanics,
...
MathWorld has
entries for over 80 Euler
terms. The entry for Euler’s theorem in the Century Dictionary
(1889-1897) began lettering them but then seemed to give up:
Euler’s theorem. (a) The proposition
that at every point of a surface the radius of curvature [rho] of a normal section
inclined at an angle [theta] to one of the principal sections is determined
by the equation [....].; so that in a synclastic surface [rho1] and [rho2] are
the maximum and minimum radii of curvature, but in an anticlastic surface, where
they have opposite signs, they are the two minima radii. (b) The proposition
that in every polyhedron (but it is not true for one which enwraps the center
more than once) the number of edges increased by two equals the number of faces
and of summits. (c) One of a variety of theorems sometimes referred to
as Euler’s, with or without further specification: as, the theorem that (xd/dx
+ yd/dy)r f(x,
y)n = nrf(x, y)n; the theorem,
relating to the circle, called by Euler and others Fermat’s geometrical theorem;
the theorem on the law of formation of approximations to a continued fraction;
the theorem of the 2, 4, 8, and 16 squares; the theorem relating to the decomposition
of a number into four positive cubes. All the above (except that of Fermat)
are due to Leonhard Euler (1707-83).
Euler introduced many other terms and symbols besides those
that bear his name. These can be found by using the Search on the front
page. On the Symbols pages see especially
Earliest Uses of Symbols of Number
Theory and Earliest
Uses of Function Symbols. For information on Euler’s writings, see the
Euler Archive.
EULER CHARACTERISTIC or EULER-POINCARÉ CHARACTERISTIC.
These terms in algebraic topology and graph theory are associated with
Poincaré’s
generalisation of Euler’s convex polyhedra formula in §16 of his "Analysis
Situs," Journal de l’École Polytechnique, 1, (1892) 1-121
See Mathworld entry.
See the entries EULER-DESCARTES RELATION and TOPLOGY.
EULER’S CIRCLES, EULER’S DIAGRAM. In about 1690
Leibniz used circle diagrams to illustrate all of the syllogisms of the
Aristotelian logic. The source is: Leibniz, De Formae Logicae
comprobatione per linearum ductus, ed. in: L. Couturat, Opuscules
et fragmentes inedits de Leibniz, Paris 1903, p. 292-320. There is a
German translation in: Fragmente zur Logik. Ausgewählt,
übersetzt und erläutert von Franz Schmidt, Berlin 1960,
p.373ff.
In his 1768 Lettres a une
Princesse d'Allemagne (see letter CIII) Euler used circles to
illustrate some basic propositions in logic. The device was used in many
nineteenth century textbooks on logic.
Euler’s scheme of notation is found in 1858 in
Elements of logic by Henry Coppée (1821-1895):
“Euler’s scheme of notation is altogether the one best
suited to our purpose, and we shall limit ourselves to the explanation
of that. It is essentially an arrangement of three circles, to represent
the three terms of a syllogism, and, by their combination, the three
propositions” [University of Michigan Digital Library].
Euler’s diagram appears in 1870 in Elementary Lessons
in Logic: Deductive and Inductive with copious questions and examples,
and a vocabulary of logical terms by W. Stanley Jevons:
“Euler’s diagram for this proposition may be constructed in
the same manner as for the proposition I as follows: [followed by a Venn
diagram of two interlocking circles].”
Euler’s circles appears in 1893 in Logic by
William Minto (1845-1893): “The relations between the terms in the
four forms are represented by simple diagrams known as Euler’s
circles.”
Wilfried Neumaier, James A. Landau, and John Aldrich contributed to
this entry. See also VENN DIAGRAM.
EULER’S EQUATION in the calculus of variations. L. Bolza Lectures on the
Calculus of Variations (1904, p. 22) writes that "Euler’s (differential)
equation" was given in 1744 in ch. 2 article 21 of "Methodus inveniendo lineas
curvas maximi minimore propietas." In a footnote Bolza notes that Hilbert had
referred to it as "Lagrange’s equation" but that Lagrange himself attributed
it to Euler: "cette equation est celle qu'Euler a trouvé le premier." Ouevres,
X, p. 397.
In 1848 Cayley used the term Euler’s equation: “By a method founded on that of Lagrange for the
solution of Euler’s equation.” This is from “Notes on the Abelian Integrals.—Jacobi’s System of
Differential Equations,” The Cambridge and Dublin Mathematical Journal, vol. III. (1848), pp. 51-54.
[James A. Landau]
See the entry CALCULUS OF VARIATIONS.
EULER’S EQUATION, FORMULA or IDENTITY eix = cos
x + i sin x. In A Concise History of Mathematics
(p. 120) D. J. Struik writes that Euler presented this equation in the Introductio
in analysin infinitorum of 1748 although it was "already discovered by
Johann Bernoulli and others in different forms". Struik reproduces pp. 103-4 of the
Introductio
which contain the relation. James Thomson calls it Euler’s formula
in his An Introduction to the Differential and Integral Calculus, 2nd
ed. (1849).
EULER’S GRAECO-LATIN SQUARES CONJECTURE. In his "Recherches sur une Nouvelle Espèces de Quarrés Magique" (1782)
conjectured that there exist no Graeco-Latin (or
Graeco-Roman) squares of order n= 4+k for k = 1, 2, .... The conjecture
was shown to be false by Bose,
Shrikhande, and Parker in 1959. In 1921 MacNeish used the term Euler square
for a generalisation of the Graeco-Latin square but the word is now often used
to refer to the Graeco-Latin square itself.
See Mathworld
See the entry LATIN SQUARE.
The EULERIAN INTEGRAL was named by Adrien Marie Legendre
(1752-1833) (Cajori 1919; DSB). He used Eulerian integral of the first kind
and second kind for the beta and gamma functions. Eulerian integral
appears in 1825-26 in his Traité des Fonctions elliptiques et des Intégrales
Eulériennes [James A. Landau].
See the entry BETA and GAMMA FUNCTIONS.
EULER’S METHOD. In 1791 the phrase “Euler’s method of squaring the circle” is found in
The Monthly Review, Enlarged, for February, 1791, Volume XXII number 2. [Google print search by James A. Landau]
Euler’s method appears in 1801 in The Monthly Review; or Literary Journal, Enlarged: From May to August, Inclusive, MDCCCI, volume XXXV, page 474:
“M. La Croix applies Euler’s method to equation of the fourth and fifth degree.” [Google print search by James A. Landau]
In 1829 the equation π/4 = tan-1 ½ + tan-1 ⅓ is labeled Euler’s Method in a list of
series used for determining the value of π in A Synopsis of the Principal Formulae and Results of Pure Mathematics by Charles Brooke.
[Google print search by James A. Landau]
Euler’s methods appears in 1851 in Bonnycastle’s introduction to algebra by
John Bonnycastle (1750?-1821): "Several new rules are introduced, those
of principal note are the following: ... the Solution of Biquadratics by Simpson’s
and Euler’s methods..." [University of Michigan Digital Library].
EULER’S NUMBERS (for the coefficients of a series for the secant function) were so
named by H. F. Scherk in 1825 in Vier mathematische Abhandlungen (Cajori
vol. 2, page 44). See Mathworld
for this and other senses of Euler numbers.
EULER’S THEOREM. The OED2’s earliest quotation for Euler’s theorem is from 1847
in Phil. Mag. 3rd Ser. XXX. 424: "Recent researches.., in reference
to the new analytical theory of imaginary quantities, have revived attention
to Euler’s theorem, that the sum of four squares multiplied by the sum of four
squares produces the sum of four squares"
EULER’S THEOREM on homogeneous functions was given in his Institutiones Calculi
Differentialis (1755). (F. Cajori, A History of Mathematics, p. 239.)
EULER-DESCARTES RELATION V + F - E = 2 for polyhedra. The history of this theorem is used as
a case study by Imre Lakatos Proofs and Refutations (1976). According
to Lakatos (p. 6), the relation was conjectured by
Descartes
around 1639 but first published by Euler in "Elementa Doctrinae Solidorum,"
Comment. Acad. Sci. U. Petrop. 4, (1758), 109-140, (Read in November
1750).
In his "Recherches sur les Polyèdres" (1813)
Oeuvres
II, 1, p. 16 Cauchy refers to "la théorème d’Euler."
In 1877 A Treatise on some New Geometrical Methods, Volume II by James Booth has:
Let m denote a number of polyhedrons, agglutinated together like a mass of crystals, and let S, F, E
denote the numbers of the solid angles, faces, and edges of this cluster of polyhedrons, we shall have
S + F - E = 1 + m
This is Cauchy’s theorem. When there is but one polyhedron, m=a, and we obtain Euler’s theorem.
In 1883 “Demonstration of Descartes’s Theorem and Euler’s Theorem” in Annals of Mathematics
G. B. Halsted gives Descartes’s Theorem as “Cutting by
diagonals the faces not triangles into triangles, the whole surface of any polyhedron contains a number of triangular faces four less than double the number of summits”
and gives Euler’s Theorem as “The number of faces and summits in any polyhedron taken together exceeds by two the number of its edges.”
A bracketed comment by William M. Thornton is “These theorems are substantially one; the second is also due to Descartes, having been published in 1860
in his Oeuvres inédites.” [James A. Landau]
In 1990 The Mathematical Intelligencer (vol. 12, no.
3) reported that readers of the magazine had selected V + F = E + 2 as the second-most-beautiful
theorem in mathematics. The article referred to the theorem as Euler’s formula
for a polyhedron.
See the entry TOPOLOGY.
EULER LEHMER PSEUDOPRIME. Euler pseudoprime first appears in Solved and Unsolved Problems
in Number Theory, 2nd ed. by Daniel Shanks (Chelsea, N. Y., 1979).
Euler Lehmer pseudoprime and strong Lehmer pseudoprime are found in A. Rotkiewicz, "On
Euler Lehmer pseudoprimes and strong Lehmer pseudoprimes with parameters L,Q
in arithmetic progressions," Prepr., Inst. Math., Pol. Acad. Sci.
220 (1980).
EULER-MACLAURIN FORMULA. The formula was published by Euler in 1738 in Comm. Acad.
Sci. Imp. Petrop. 6, p. 68 and by
Colin
Maclaurin in 1742 in Treatise of Fluxions p. 672. (According to E.
T. Whittaker and G. Robinson The Calculus of Observations (1924, p. 135.))
Both men had discovered the result somewhat earlier; see MacTutor’s
Leonhard
Euler for an account.
Euler-Maclaurin formula is found in 1872 in
A Treatise on the Calculus of Finite Differences by George Boole, 2nd ed. edited by J. F. Moulton. [Google print search by James A. Landau]
EULER-MASCHERONI CONSTANT. See the entry on the
Euler-Mascheroni
constant on the Earliest
Uses of Symbols for Constants for references to the writings of Euler and
Mascheroni.
Euler’s constant appears in 1868 in the title "On the Calculation of the Numerical
Value of Euler’s Constant, Which Professor Price, of Oxford, Calls E,"
Proc.
of R. Soc Lond. XV. 429-432. (JSTOR) Eulerian constant
appears in the Century Dictionary (1889-1897).
In 1872, "On the History of Euler’s Constant" by
J. W. L. Glaisher in The Messenger of Mathematics has: "It has sometimes
(as in Crelle, t. 57, p. 128) been quoted as Mascheroni’s constant, but
it is evident that Euler’s labours have abundantly justified his claim to its
being named after him."
In his famous address
in 1900, David Hilbert (1862-1943) used the term Euler-Mascheroni constant
(and the symbol C).
EVEN FUNCTION. Functiones pares is found in 1727 in "Problematis
traiectoriarum reciprocarum solutio," presented to the Petersburg Academy in
July 1727 by Leonhard Euler:
Primo loco notandae sunt functiones, quas pares appello, quarum haec est
proprietas, ut immutatae maneant, etsi loco x ponatur -x. [In the first place are
noted functions, which I call even, of which there is this property, that they remain
unchanged if in place of x is put -x.]
This citation was found by Ed Sandifer.
Even function is found in English in 1809 in a translation of Legendre’s 1792 paper “Mémoire
Sur Les Transcendantes Elliptiques.” [James A. Landau]
EVENT has been in probability in English from the beginning. A. De Moivre’s
The Doctrine of Chances (1718) begins "The Probability of an Event is greater
or less, according to the number of chances by which it may happen, compared with the
whole number of chances by which it may either happen or fail."
Event took on a technical existence when Kolmogorov in the
Grundbegriffe der Wahrscheinlichkeitsrechnung
(1933) identified "elementary events" ("elementare Ereignisse") with the elements of a collection
E (now called the "sample space") and "random events" ("zufällige Ereignisse")
with the elements of a set of subsets of E [John Aldrich].
The term EVOLUTE was defined by Christiaan Huygens (1629-1695)
in 1673 in Horologium oscillatorium. He used the Latin
evoluta. He also described the involute, but used the phrase
descripta ex evolutione [James A. Landau].
Evolute and anti-evolute are found in 1717 in English in
The Lives of the French, Italian and German Philosophers.
[Google print search by James A. Landau]
EXACT DIFFERENTIAL EQUATION.
Exact differential is found in 1824 in
First
Principles of the Differential and Integral Calculus, or the Doctrine of Fluxions, Intended as an Introduction to the Physico-Mathematical Sciences; Taken Chiefly from the Mathematics of Bézout,
And translated from the French For the Use of the Students of the University at Cambridge, New England:
“But when the numerator is the differential of the denominator, multiplied or divided by a constant number, the proposed differential must be decomposed into two factors, of which one shall be
a fraction having for its numerator the exact differential of the denominator, and the other a constant number.”
Exact differential equation is found in 1858 in
A Treatise
on Differential Equations and on the Calculus of Finite Differences, 2nd ed., by J. Hymers.
[Google print searches by James A. Landau]
EXCENTER, EXCIRCLE. See the entry CIRCUMCENTER, CIRCUMCIRCLE, EXCENTER, EXCIRCLE, INCENTER, INCIRCLE, MIDCIRCLE.
Interest in EXCHANGEABLE random variables dates from the 1920s with
Bruno de Finetti (1906 - 1985)
the most influential contributor. However "exchangeable" emerged
only slowly as the standard term. De Finetti used "équivalent" in his most widely read work,
"La
prévision: ses lois logiques, ses sources subjectives," Annales
de l'Institute Henri Poincaré, 7, (1937) 1-68.
L. J. Savage The Foundations
of Statistics (1954) used the term "symmetric." Polyá suggested
the term "échangeable" and it appeared in a 1943 book by Fréchét.
De Finetti took up the term and "exchangeable" was adopted in the
1964 English translation of his 1937 work. David (2001) cites M. Loève’s Probability
Theory (1955) for the first occurrence of "exchangeable" in the English literature.
[This entry was contributed by John Aldrich, based on J. von Plato Creating Modern Probability (1994).]
EXCIRCLE was used in 1883 by W. H. H. Hudson in Nature
XXVIII. 7: "I beg leave to suggest the following names: circumcircle,
incircle, excircle, and midcircle" (OED2).
EXHAUSTION, METHOD OF. See METHOD OF EXHAUSTION.
The expression EXHAUSTIVE ESTIMATION was used by R. A. Fisher in his 1936 address
Uncertain Inference
Proceedings of the American
Academy of Arts and Science, 71: 245-258. Fisher borrowed the phrase
from the book Méthodes d'Estimation by
G. Darmois where exhaustif was
used to translate Fisher’s term sufficient.
Fisher wrote to Darmois, “I notice you use the term ‘exhaustive estimation’ for
what I speak of as ‘sufficient statistics’. I should like, if you approve, to
use the term ‘exhaustive estimation’ in a somewhat wider sense, including not
only the cases in which sufficient statistics, but also those cases … in which
the whole of the ancillary information may be utilised by taking account of
characteristics of the sample, which, by themselves, yield no information
respecting the parameter sought.”
Correspondence p. 65.
See the entries SUFFICIENCY and ANCILLARY.
EXPECTATION. The tract by Christiaan
Huygens, in Latin De Ratiociniis in Ludo Aleae (1657), is about calculating
expectations and the concept of expectation has been attributed to him,
although A. W. F. Edwards (Pascal’s Arithmetical Triangle) argues that
Pascal had already developed it.
The term "expectation" was used neither by Pascal nor by Huygens. The
latter’s Dutch text has no term that translates as "expectation;" it speaks
rather of the "value" of a game. Expectatio appears in the Latin translation
by van Schooten and expectation appears in the
English translation
of the Latin. The translators, however, do not use these terms in the modern way. Huygens’s Proposition
I is rendered, "If I expect a or b, and have an equal chance of
gaining either of them, my Expectation is worth (a + b)/2." The
"worth or "value" of the expectation is the modern concept of expectation. The
same phraseology is used in De Moivre’s Doctrine of Chances (1718), although
"the expectation is worth" is often shortened to "the expectation is."
The expression "l'espérance mathématique," or mathematical
expectation, with its modern meaning is found in a letter by Gabriel Cramer
dated 21st May 1728: see letter 8 in
Correspondence
of Nicholas Bernoulli concerning the
St Petersburg game with Montmort, Daniel Bernoulli and Cramer
(translation by Richard J. Pulskamp.)
Laplace adopted "l'espérance
mathématique" along with Cramer’s complementary term, "l'espérance morale":
see his Théorie Analytique des Probabilités, livre II, chapitre I,
p. 189.
The English "mathematical expectation"
appears in A. de Morgan’s Essay on Probabilities (1838, p. 97), "The
balance is the average required, and is known by the name of the mathematical
expectation." (OED).
In the course of the 19th century the qualification
"mathematical" became optional, perhaps because "moral expectation" fell out
of use. The term "expected value" came into use in the 20th century.
The OED gives a quotation from Arne Fisher’s Mathematical Theory of Probabilities
(1915) p. 97, "Russian and Scandinavian
writers and the followers of the Lexis statistical school of Germany have preferred
to make another quantity known as the ‘probable' or ‘expected value', the nucleus
of their investigations.." Fisher uses expected value as the general term, reserving
expectation for situations where a sum of money is involved.
See also MORAL EXPECTATION and the discussion
of EXPECTATION on the
Symbols in Probability and Statistics page.
[This entry was contributed by John Aldrich, based on Edwards (op. cit.) and Hald (1986)]
The term EXPERIMENT has been used in expositions
of probability theory since W. Feller adopted it in his Introduction
to Probability Theory and its Applications, volume one (1950): "The
mathematical theory of probability gains practical value and an intuitive meaning
in connection with real or conceptual experiments or phenomena such as [a long
list of examples follows]." (p. 8)
See SAMPLE SPACE.
EXPERIMENTS, DESIGN OF in Statistics. See DESIGN OF EXPERIMENTS.
EXPLEMENT is found in 1827 in Mathematical and astronomical tables
by William Galbraith: "...the explement, or difference from four right angles"
[Google print search].
See also CONJUGATE ANGLE.
EXPLICIT FUNCTION is found in 1814 New Mathematical and
Philosophical Dictionary: "Having given the methods ... of
obtaining the derived functions, of functions of one or more
quantities, whether those functions be explicit or implicit, ... we
will now show how this theory may be applied" (OED2).
EXPLORATORY DATA ANALYSIS is the title of J. W. Tukey’s 1971 book Exploratory Data Analysis
volume 1. Exploratory data analysis is "about looking at data to see what it seems
to say," while confirmatory data analysis is about "assessing the precision
with which our inference from sample to population is made."
David (2001). See DATA ANALYSIS and DESCRIPTIVE
STATISTICS.
The term EXPONENT was introduced by Michael Stifel (1487-1567)
in 1544 in Arithmetica integra. He wrote, "Est autem 3
exponens ipsius octonarij, & 5 est exponents 32 & 8 est
exponens numeri 256" (Smith vol. 2, page 521).
Exponent is found in English in 1745 in Sir
Isaac Newton’s Two Treatises of the Quadrature of Curves, and Analysis by Equations of an infinite Number of Terms, explained by John Stewart:
“Wherefore universally the Rule for finding the Fluxion of any Power of a flowing Quantity, be it’s
Exponent positive or negative, integral or fractional, and whether the Quantity affected by the Exponent be simple or compound, is this, multiply the flowing Quantity by the Exponent of the Power, diminish the Exponent by a Unity, and multiply
further by the Fluxion of the Quantity or Root.” [Google print search by James A. Landau]
In the 1771 edition of the
Encyclopaedia Britannica, exponent is spelled differently (in the Logarithm article):
"Dr. Halley, in the philosophical transactions, ... says, they are
the exponements of the ratios of unity to numbers" [James A. Landau].
EXPONENTIAL is found in English in 1704
in John Harris, Lexicon Technicum: "Exponential curves are such as partake both of the nature of Algebraick and Transcendent ones"
(OED2).
In Statistics the adjective EXPONENTIAL has been attached
to several objects--including at times the normal distribution. Today the most
common constructions are:
Exponential distribution. David
(2001) cites Karl Pearson’s reference to the "negative exponential curve"
on p. 345 of his
"Contributions
to the Mathematical Theory of Evolution. II. Skew Variation in Homogeneous Material,"
Philosophical Transactions of the Royal Society of London. A, 186.
(1895), 343-414.
Double exponential distribution. David (2001) cites R. A. Fisher
A Mathematical
Examination of the Methods of Determining
the Accuracy of an Observation by the Mean Error, and by the Mean Square Error.
(1920, p. 770) for the double exponential frequency curve. Laplace discussed
this function in 1774 and it has been known as "the first law of
Laplace" (with the normal distribution as the second.) Other names include the bilateral exponential
and two-tailed exponential.
Exponential family (of distributions). In 1934/6 several authors including
R. A. Fisher,
G. Darmois,
E. J. Pitman and
B. O. Koopman
discussed the type of distribution for which a sufficient statistic exists: in Koopman’s
words, such distributions are of a "very special exponential type."
The papers are Fisher
Two new
properties of mathematical likelihood, Proc.
Roy. Soc., A, 144 (1934), 285-307, Darmois
’sur les lois de probabilité à estimation exhaustive',
C.R. Acad. Sci. 200, (1935), 1265-1266,
Pitman "Sufficient statistics and intrinsic accuracy," Proceedings of the
Cambridge Philosophical Society, 32, (1936), 567-579 and
Koopman "On Distributions admitting a sufficient statistic"
Transactions of the American Mathematical Society, 39, (1936), 399-409. Since around
1950 it has been common to refer to the exponential family of distributions.
David (2001) cites M. A. Girshick & L. J. Savage "Bayes and minimax estimates for quadratic loss functions."
Proceedings of the 2nd Berkely Symposium, (1951) 43-73.
Also used are names on the pattern "Fisher-Pitman-Koopman-Darmois family,"
though usually without all of the names.
[This entry was contributed by John Aldrich]
EXPONENTIAL CURVE is found in 1704 in Lexicon technicum, or
an universal English dictionary of arts and sciences by John
Harris (OED2).
EXPONENTIAL FUNCTION. This term was used by Jakob Bernoulli,
according to an Internet web page.
Lacroix used fonctions exponentielles in Traité
élémentaire de calcul différentiel et de calcul
intégral (1797-1800).
Exponential function appears in 1831 in the second edition of
Elements of the Differential Calculus (1836) by John Radford
Young: "Thus, ax, a log x, sin
x, &c., are transcendental functions: the first is an
exponential function, the second a logarithmic
function, and the third a circular function" [James A. Landau]
EXTERIOR ANGLE is found in English in 1658 in
John Newton
Trigonometria Britanica: Or The Doctrine of Triangles, in Two Books:
“Therefore any two angles of a triangle are lesse then two right. And any side being continued, the exterior angle is equal to the two interior opposite ones.”
[Google print search by James A. Landau]
EXTRANEOUS ROOT is found in 1843 in Theory and Solution of Algebraical Equations of the Higher Orders,
2nd ed., by John Radford Young: “In the researches of Fourier, so
fully discussed in Chapters VIII and IX, we have seen that the object
first to be accomplished, in the analysis of a doubtful interval, is to
reduce the last three of the indices to the values 0, 1, 2. Till we get
three such consecutive indices, either for the three final functions, or
for some preceding three, Fourier’s peculiar method of proceeding does
not come into operation. In bringing about this [page 301] arrangement
of indices, the proposed interval must be narrowed, with a view to the
detection of the situations of those roots of the derived equations
which require to be passed over, or separated, before the desired
arrangement can be present. In the search after these extraneous roots,
in the proposed interval, we are not supplied by Fourier, with any
guide. ...” [Google print search by James A. Landau]
The term EXTREMAL (for a resolution curve) was introduced by
Adolf Kneser (1862-1930), who also introduced these other terms in
the calculus of variations: field (for a family of extremals),
transversal, strong and weak extremum (DSB). The term apparently is in his Lehrbuch der Variationsrechnung (1900).
Extremal is found in English in 1901 in
“Sufficient Conditions in the Calculus of Variations”
by W. F. Osgood in Annals of Mathematics:
“Any function y of x (or curve representing such a function) which, at all interior points of an interval (x’, x”) throughout which it is considered satisfies Lagrange’s equation (2) is called an extremal.”
[Google print search by James A. Landau]
EXTREME VALUE appears in E. J. Gumbel, "Les valeurs extrêmes des distributions statistiques,"
Ann. Inst.
H. Poincaré, 5 (1935), 115-138.
See also L. H. C. Tippett, "On the extreme individuals and the range
of samples taken from a normal population," Biometrika 17
(1925) [James A. Landau].
See also WEIBULL DISTRIBUTION.
EXTREMUM was first used as a mathematical term (in German) by
Paul
Du Bois-Reymond (1831-1889) in German in 1879 in "Fortsetzung der
Erläuterungen zu den Anfangsgründen der Variationsrechnung,"
Math.
Ann. XV. 564, according to the OED2.
Extremum was used in English in 1904 by Oskar Bolza (1857-1942) in
Lectures on the Calculus of Variations
p. 10: "The word 'extremum' will be used for maximum and minimum alike, when
it is not necessary to distinguish between them" (OED2).
Front -
A -
B -
C -
D -
E -
F -
G -
H -
I -
J -
K -
L -
M -
N -
O -
P -
Q -
R -
S -
T -
U -
V -
W -
X -
Y -
Z -
Sources
 and vector x together in the value/vector-equation Ax =
and vector x together in the value/vector-equation Ax =  x :
any value
x :
any value  for which this equation is satisfied for a non-null x
is a value and the associated x is a vector. The existence of a non-null solution x
for (A -
for which this equation is satisfied for a non-null x
is a value and the associated x is a vector. The existence of a non-null solution x
for (A -  I)x = 0 requires the determinant of
(A -
I)x = 0 requires the determinant of
(A -  I) to be zero, i.e. that the roots of a polynomial
are significant. This finite-dimensional case is used to motivate the treatment of differential equations
and integral equations which involve infinite-dimensional spaces where the vector is now a function. The
historical order of development was more or less the reverse. The polynomial equation generated from the
differential equations of celestial mechanics came first, ca. 1780, then the equation was expressed using
determinants ca. 1830, then the equation was associated with matrices ca. 1880, then integral equations were
studied ca. 1900 until finally the modern order of topics starting from the value/vector-equation became established
ca. 1940. (Based on Kline ch. 29, 33, 45 & 46 and Hawkins (1975 and -7.))
I) to be zero, i.e. that the roots of a polynomial
are significant. This finite-dimensional case is used to motivate the treatment of differential equations
and integral equations which involve infinite-dimensional spaces where the vector is now a function. The
historical order of development was more or less the reverse. The polynomial equation generated from the
differential equations of celestial mechanics came first, ca. 1780, then the equation was expressed using
determinants ca. 1830, then the equation was associated with matrices ca. 1880, then integral equations were
studied ca. 1900 until finally the modern order of topics starting from the value/vector-equation became established
ca. 1940. (Based on Kline ch. 29, 33, 45 & 46 and Hawkins (1975 and -7.))
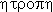 , a transformation. I have
intentionally formed the word entropy so as to be as similar as possible
to the word energy, since both these quantities, which are to be known
by these names, are so nearly related to each other in their physical significance
that a certain similarity in their names seemed to me advantageous.
, a transformation. I have
intentionally formed the word entropy so as to be as similar as possible
to the word energy, since both these quantities, which are to be known
by these names, are so nearly related to each other in their physical significance
that a certain similarity in their names seemed to me advantageous.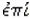 upon +
upon + 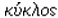 circle. The earliest
quotation in the OED is from Chaucer’s Treatise on the Astrolabe (about 1391): “The Moone Moeuyth the contrarie from othere planetes as in hire
Episicle.”
circle. The earliest
quotation in the OED is from Chaucer’s Treatise on the Astrolabe (about 1391): “The Moone Moeuyth the contrarie from othere planetes as in hire
Episicle.”
 .
The Arabic term was used by many later algebraists in the Islamic world. The Latin equatio is probably a translation from the Arabic.
[Jeffrey A. Oaks]
.
The Arabic term was used by many later algebraists in the Islamic world. The Latin equatio is probably a translation from the Arabic.
[Jeffrey A. Oaks]