Earliest Known Uses of Some of the Words of Mathematics (P)

Last revision: Aug. 7, 2018

p-ADIC INTEGER was coined by Kurt Hensel (1861-1941) (Katz, page 824).

The p* FORMULA, also called Barndorff-Nielsen’s formula, was introduced by Ole Barndorff-Nielsen in his article “On a Formula for the Distribution of the Maximum Likelihood Estimator,” Biometrika, 70, (1983), 343-365.

P-VALUE and prob-value. David (1995) discusses the difficulties in dating P-value, the idea of which goes back to Laplace--at least--before opting for a reference from 1960! Subsequently David (1998) chose W. E. Deming’s Statistical Adjustment of Data of 1943. When Deming wrote the phrase "value of P" was current. It was used in Karl Pearson’s (1900) "On the Criterion that a Given System of Deviations from the Probable in the Case of Correlated System of Variables is such that it can be Reasonably Supposed to have Arisen from Random Sampling" (Philosophical Magazine, 50, 157-175) and used very heavily in R. A. Fisher’s Statistical Methods for Research Workers (1925). The use of P-values (or prob-values) is often set against the use of fixed significance levels, especially 5%. It is ironical then that the "value of P" should feature so strongly in Fisher’s book when that work also did so much to popularise the use of the 5% level. [John Aldrich]

See also SIGNIFICANCE and HYPOTHESIS AND HYPOTHESIS TESTING.

PAIRWISE. A JSTOR search found the term in P. Jordan; J. v. Neumann; E. Wigner “On an Algebraic Generalization of the Quantum Mechanical Formalism,” Annals of Mathematics, 35, (1934), 29-64. The phrase “a set of pairwise orthogonal unit elements” appears on p. 35.

PANGEOMETRY is the term Nicholas Lobachevsky (1796-1856) gave to his non-Euclidea geometry (Schwartzman, p. 157).

PARABOLA was probably coined by Apollonius, who, according to Pappus, had terms for all three conic sections. Michael N. Fried says there are two known occasions where Archimedes used the terms “parabola” and “ellipse,” but that “these are, most likely, later interpolations rather than Archimedes own terminology.”

However, G. J. Toomer believes the names parabola and hyperbola are older than Apollonius, based on an Arabic translation of Diocles’s On burning mirrors.

PARABOLIC GEOMETRY. See hyperbolic geometry.

PARACOMPACT. The term and the concept are due to J. Dieudonné (1906-1992), who introduced them in Une généralisation des espaces compacts, J. Math. Pures Appl., 23 (1944) pp. 65-76. A topological space X is paracompact if (i) X is a Hausdorff space, and (ii) every open cover of X has an open refinement that covers X and which is locally finite. The usefulness of the concept comes almost entirely from condition (ii), while the role of condition (i) has been somewhat controversial. Thus, in his book General Topology (1955), John Kelley (p. 156) replaces (i) by the condition that X be regular (and his definition of regularity does not include the Hausdorff separation axiom), while some other authors do not even mention (i) in defining paracompactness. In any case, however, it is possible to state this important fact (conjectured by Dieudonné in the paper above): every metric space is paracompact. This was proved by A. H. Stone in Paracompactness and product spaces, Bull. Amer. Math. Soc., 54 (1948) 977-982. [This entry was contributed by Carlos César de Araújo.]

PARACONSISTENT LOGIC. The first formal calculus of inconsistency-tolerant logic was constructed by the Polish logician Stanislaw Jaskowski, who published his paper "Propositional calculus for contradictory deductive systems" (in Polish) in Studia Societatis Scientiarum Torunensis, 55--77 in 1948. It was reprinted in English in Studia Logica 24, 143--157 (1969).

Newton Carneiro Affonso da Costa, one of the most prominent researchers in paraconsistent logic, referred to it as inconsistent formal systems in his 1964 thesis, which used that term as its title. [See the introduction of the work "Sistemas Formais Inconsistentes", Newton C. A. da Costa, Editora da UFPr, Curitiba, 1993, p. viii. This work is a reprint of the Prof. Newton’s original 1964 thesis, the initial landmark of all studies in the matter.

The term paraconsistent logic was coined in 1976 by the Peruvian philosopher Francisco Miró Quesada, during the Terceiro Congresso Latino Americano.

[Manoel de Campos Almeida, Max Urchs]

PARADOX is a label fixed to many arguments in Mathematics. See e.g. BANACH-TARSKI PARADOX, HAUSDORFF PARADOX, RUSSELL’S PARADOX, ST. PETERSBURG PARADOX, SIMPSON’S PARADOX, ZENO’S PARADOXES.

Paradox (from the Greek for contrary to received opinion) is an exasperatingly ambiguous word and it is not unusual to read statements like, "This is not a paradox at all, the only reason that it is given this name is that it is counter-intuitive." W. V. Quine Ways of Paradox (1966) classifies paradoxes, distinguishing 3 types:

• A veridical paradox produces a result that appears absurd but is demonstrated to be true nevertheless. E.g. SIMPSON’S PARADOX.
• A falsidical paradox produces a result that not only appears false but actually is false; there is a fallacy in the argument. E.g. ZENO’S PARADOXES.
• An antinomy (from the Greek for against law) produces a self-contradiction by accepted ways of reasoning. E.g. RUSSELL’S PARADOX.

The examples are taken from these pages. The placing of a paradox can be a matter of dispute. Quine notes, "One man’s antinomy can be another man’s veridical paradox, and one man’s veridical paradox can be another man’s platitude." For further discussion see BANACH-TARSKI PARADOX and HAUSDORFF PARADOX.

Paradoxes have been discussed since antiquity; see the LIAR PARADOX. In the Middle Ages variants of the Liar paradox were studied under the heading insolubilia (W. & M. Kneale The Development of Logic (1962) pp. 227-8). The early 20^th century with its disputes on set theory and logic was the great age for paradoxes. Amongst the antinomies discovered then were those of BURALI-FORTI, RUSSELL and RICHARD.

Logical and semantic paradoxes. F. P. Ramsey pointed out that the "contradictions fall into two fundamentally distinct groups." ("Foundations of Mathematics" in Foundations of Mathematics and Other Essays (1931, pp. 20-1)) Ramsey’s Type A are now called the logical paradoxes and his Type B the semantic paradoxes: RUSSELL’S PARADOX is an example of the first and RICHARD’S PARADOX an example of the second. A JSTOR search found the logical/semantic terminology in use in W. V. Quine’s review of The New Logic by Karl Menger et al. in the Journal of Symbolic Logic, 3, (1938), p. 48.

This entry was contributed by John Aldrich.

PARALLEL appears in English in 1549 in Complaynt of Scotlande, vi. 47: "Cosmaghraphie ... sal delcair the eleuatione of the polis, and the lynis parallelis, and the meridian circlis" (OED2).

PARALLELEPIPED. According to Smith (vol. 2, page 292), "Although it is a word that would naturally be used by Greek writers, it is not found before the time of Euclid. It appears in the Elements (XI, 25) without definition, in the form of ’sparallelepipedal solid,’s the meaning being left to be inferred from that of the word ’sparallelogrammic’s as given in Book I."

Parallelipipedon appears in English in 1570 in Sir Henry Billingsley’s translation of Euclid’s Elements.

In the 1644 edition of his Cursus mathematicus (in Latin), Pierre Herigone used the spelling parallelepipedum.

The first citation in the OED2 with the shortened spelling parallelepiped is Walter Charleton (1619-1707), Chorea gigantum, or, The most famous antiquity of Great-Britain, vulgarly called Stone-heng : standing on Salisbury Plain, restored to the Danes, London : Printed for Henry Herringman, 1663.

Charles Hutton’s Dictionary (1795) shows parallelopiped and parallelopipedon.

In Noah Webster’s A compendious dictionary of the English language (1806) the word is spelled parallelopiped.

Mathematical Dictionary and Cyclopedia of Mathematical Science (1857) has parallelopipedon.

U. S. dictionaries show the pronunciation with the stress on the penult, but some also show a second pronunciation with the stress on the antepenult.

PARALLELOGRAM appears in English in 1570 in Sir Henry Billingsley’s translation of Euclid’s Elements (OED2).

In 1832 Elements of Geometry and Trigonometry by David Brewster, which is a translation of Legendre, has:

The word parallelogram, according to its etymology, signifies parallel lines; it no more suits the figure of four sides than it does that of six, of eight, &c. which have their opposite sides parallel. In like manner, the word parallelopipedon signifies parallel planes; it no more designates the solid with six faces, than the solid with eight, ten, &c. of which the opposite faces are parallel. The names parallelogram and parallelelopipedon*, have the additional inconvenience of being very long. Perhaps, therefore, it would be advantageous to banish them altogether from geometry; and to substitute in their stead, the names rhombus and rhomboid, retaining the term lozenge, for quadrilaterals whose sides are all equal.

PARAMETER. Claude Mydorge used the word parameter with the meaning of "latus rectum" on page 3 of “Prodromi catoptricorum et dioptricorum sive conicorum operis libri primus et secundus,” Paris 1631. [Alessio Martini, Siegmund Probst]

A reference to Mydorge’s term is in Frans van Schooten, “In geometriam Renati Descartes commentarii,” 1659, printed in: Geometria, a Renato Des Cartes anno 1637 gallice edita, postea autem una cum notis Florimondi de Beaune (...) in latinam linguam versa et commentariis illustrata opera atque studio Francisci a Schooten (...) Nunc demum ab eodem diligenter recognita, locupletorioribus commentariis instructa, multisque egregiis accessionibus (...) exornata. 2 vols. Amsterdam 1659-1661, vol. I, p. 208.

According to Kline (page 340), parameter was introduced by Gottfried Wilhelm Leibniz (1646-1716). He used the term in 1692 in Acta Eruditorum 11 (Struik, page 272). Kline used the term in its modern sense. According to Siegmund Probst, Frans van Schooten is probably the source that Leibniz used (numerous references since 1673); starting in 1673 Leibniz used parameter for constants in formulas with variables, e.g. equations of curves or series. See Leibniz volumes VII,3 VII,4 VII,5.

PARAMETER (in statistics) Although parameter had been used by earlier writers--David (2001) cites J. C. Kapteyn Skew Frequency Curves in Biology and Statistics (1903)--it was established as the standard term by R. A. Fisher. He introduced it, along with many other terms, in "On the Mathematical Foundations of Theoretical Statistics", Philosophical Transactions of the Royal Society of London, Ser. A. 222, (1922) 309-368.

Parameter arrived with statistic for Fisher saw the need for two terms (p. 311):

it has happened that in statistics a purely verbal confusion has hindered the distinct formulation of statistical problems; for it is customary to apply the same name, mean, standard deviation, correlation coefficient, etc. both to the true value which we should like to know but can only estimate, and to the particular value at which we arrive by our method of estimation ...

Parameter did not replace any existing standard term. Fisher had used "arbitrary element" (1912) and "population-character" (1921), while Karl Pearson’s "frequency-constant" could mean either a parameter or a statistic.

While Fisher’s use of statistic was criticised (See entry on Statistic), parameter fell in with an established usage, which the OED2 traces to the mid-nineteenth century, viz. "a quantity which is constant (as distinct from the ordinary variables) in a particular case considered, but which varies in different cases."

The use of the terms parametric and nonparametric for different kinds of hypotheses dates from the 1940s. See the entry NONPARAMETRIC.

See also STATISTIC and NUISANCE PARAMETER AND PARAMETER OF INTEREST.

[This entry was contributed by John Aldrich, using Hald (1998).]

PARAMETRIC EQUATION is found in 1894 in "On the Singularities of the Modular Equations and Curves" by John Stephen Smith in the Proceedings of the London Mathematical Society [University of Michigan Historical Math Collection].

PARETO DISTRIBUTION, PARETO’S LAW. In the 1890s the economist Vilfredo Pareto (1843-1925) found a pattern in the way incomes were distributed within countries. "La courbe des revenus" is given by

log N = log A - α log x

where N is the number of individuals with incomes higher than x, and A and α are constants. In his Cours d’séconomie politique (1897) Pareto described the curve and provided evidence of its wide applicability. Economists were soon referring to Pareto’s "law of the distribution of income" though they did not necessarily agree that it constituted a law; see e.g. Henry L. Moore "The Statistical Complement of Pure Economics," Quarterly Journal of Economics, 23, (1908), 1-33. The formula can be rewritten as a frequency distribution and statisticians found it natural to refer to "Pareto’s distribution;" see e.g. J. O. Irwin "Recent Advances in Mathematical Statistics (1934)," Journal of the Royal Statistical Society, 99, (1936), 714-769. [John Aldrich]

PARTIAL DERIVATIVE and PARTIAL DIFFERENTIAL. Partial derivatives appear in the writings of Newton and Leibniz.

Partial differential equation was used in 1770 by Antoine-Nicolas Caritat, Marquis de Condorcet (1743-1794) in the title "Memoire sur les Equations aux différence partielles," which was published in Histoire de L’sAcademie Royale des Sciences, pp. 151-178, Annee M. DCCL&ldquo:III (1773).

Partial differential equation appears in English in 1809 in a letter from “Mr. Thomas Knight, Of Papcastle, near Cockermouth” in The Mathematical Repository, New Series, Volume III (1809). The same issue of The Mathematical Repository contains the expression partial fluxion. [James A. Landau]

An early use of the term partial derivative in English is in an 1834 paper by Sir William Rowan Hamilton [James A. Landau].

Partial differential equation is found in English in 1820 in A Collection of Examples of the Applications of the Differential and Integral Calculus by George Peacock: "Given a solution of a partial differential equation, to find whether it is included in the general solution or not." [Google print search]

See the Earliest Uses of Symbols of Calculus page.

PARTIAL FRACTION. Fraction partielle occurs in Legendre’s 1792 paper Mémoire Sur Les Transcendantes Elliptiques: “que chaque fraction partielle soit de la forme N / (1 + n sin² φ)^k, n et N étant des coéfficiens constans reels ou imaginaires.”

In English partial fraction appears in the 1809 translation of Legendre’s 1792 paper, which translates the above French text as “that every partial fraction shall be of the form N / (1 + n sin² φ)^k, n and N being constant coefficients, real or imaginary.”

[James A. Landau]

PARTIAL PRODUCT is found in English in an 1822 translation of Elements of Algebra by Euler. [Google print search]

PARTICULAR SOLUTION is found in 1735-6 Phil. Trans. 39, 325:

In the Author’s second Problem, or the Relation of the Fluxions being given to determine the Relation of the Fluents,..he [sc. Newton] begins with a particular Solution of it. He calls this Solution particular, because it extends only to such Cases, wherein the given Fluxional Equation either has been, or might have been, derived from some previous finite Algebraical Equation.

The term particular case of the general integral is due to Lagrange (Kline, page 532).

Particular integral is found in English in 1814 in New Mathematical and Philosophical Dictionary by P. Barlow:

Particular Integral, in the Integral Calculus, is that which arises in the integration of any differential equation, by giving a particular value to the arbitrary quantity or quantities that enter into the general integral (OED2).

Montmort (Essay d’sanalysis sur les jeux de hazard, 1708) was the first to attach Pascal’s name to the triangle, "Table de M. Pascal pour les combinaisons,"  while De Moivre (Miscellanea analytica, 1730) used the expression "Triangulum Arithmeticum PASCALIANUM."  (From Edwards op. cit.) Montmort and De Moivre both wrote on probability and the application of the triangle to this field was an important new element in the Traité. Indeed the Traité was one of the founding works of probability.

Arithmetical triangle of Pascal is found in Ed. Lucas, "Note sur le triangle arithmétique de Pascal et sur la série de Lamé, N. C. M. (1876). Pascal’s triangle appears in 1886 in Algebra by George Chrystal (1851-1911). 

While triangle research in Western Europe only gained momentum in the Renaissance, there was much earlier work in India, Persia and China. In India there was a tradition beginning with Pingala (ca 200BC). His rule for finding the number of combinations, known as the Meru Prastara (Staircase of Mount Meru), was put into triangular form by the 10^th century AD. (Roger Cooke and Edwards op. cit.)

In Persia and China the binomial theorem seems to have been discovered around 1100. In China the triangle is called Yang Hui’s triangle. The ’sPascal’s triangle as depicted in A.D. 1303 tabulates the binomial coefficients up to the eighth power. See Materials for the History of Statistics for the full reference.

(Based on Edwards’s Pascal’s Arithmetical Triangle.)

See the entries on COMBINATION and PROBABILITY.

PASCAL’S WAGER, an argument for acting as if one believed in God, has been claimed as "the first well-understood contribution to decision theory" (Hacking (1975, ch. 8)). The argument was published in the Pensées, a work assembled from Pascal’s notes after his death; see Infinite--nothing (§233). The argument was discussed by Leibniz, Locke, Voltaire and Diderot as well as by religious writers. The argument never became part of the probability literature but it received renewed attention in the 20^th century with the rise of decision theory. See Pascal’s wager in the Stanford Encyclopedia.

A Google print search finds Pascal’s wager in 1896 in The New World: A Quarterly Review of Religion, Ethics, and Theology, volume 5: “In Pascal’s Thoughts there is a celebrated passage known in literature as Pascal’s wager.”

PATH ANALYSIS is the modern term for what Sewall Wright called the method of path coefficients in his paper "Correlation and Causation," Journal of Agricultural Research, 20, (1921), 557-585. Wright introduced the method as follows, "In the biological sciences, especially, one often has to deal with a group of characteristics or conditions which are correlated because of a complex of interacting, uncontrollable, and often obscure causes.... The present paper is an attempt to present a method of measuring the direct influence along each separate path in such a system and thus of finding the degree to which variation of a given effect is determined by each particular cause." (p. 557) The term path analysis seems to have become common only around 1960. (JSTOR search.)

PATHOLOGICAL as “satisfying the conditions of a theory or theorem but contrary to intuition as to the general nature of the objects concerned, and therefore regarded as bizarre or defective.” (Borowski & Borwein)

The word has been in English as a medical term since the 17^th century but its use as a mathematical term of art appears to date from the 1930s. A JSTOR search found Murray and von Neumann writing in “On Rings of Operators,” Annals of Mathematics, 37, (1936), p. 227 of another “pathological” possibility. The authors put quotes around the word but they quickly became superfluous. The OED’s earliest citation is from I. S. Sokolnikoff Advanced Calculus (1939): “Such pathological behavior of continuous functions led to a careful inquiry into the meaning of such geometrical concepts as the area under a curve.”m [John Aldrich]

See the entry WELL-BEHAVED.

PAULI MATRICES are named after the physicist Wolfgang Pauli, who used them in his “Zur Quantenmechanik des magnetischen Elektrons,” Zeitschrift für Physik, 43, (1927), p. 60. However they had appeared long before in Cayley’s “A Memoir on the Theory of Matrices” (1858) Coll Math Papers, II, 475-96. In paragraph 45 (p. 491) Cayley writes that these matrices satisfy a system of relations “precisely similar to that in the theory of quaternions.” See the Encyclopedia of Mathematics entry Pauli matrices.

See MATRIX, MATRIX MECHANICS and QUATERNIONS.

PEANO’S AXIOMS for arithmetic were presented by Giuseppe Peano in Arithmetices Principia (1889) translated from the Latin in Heijenoort (1967, pp. 83-107). Grattan-Guinness (2000, p. 228) notes that, while Peano refers to Dedekind’s booklet Was sind und Was sollen die Zahlen? (1887) Works, 3, 335-391, he later said he had found his axiom system independently. B. Russell Principles of Mathematics (1903) refers to "Peano’s primitive propositions."

The PEANO CURVE was presented by Peano in "Sur une courbe, qui remplit une aire plane." Math. Ann. 36, 157-160, 1890. Alas there are no diagrams!

The term PEANO-GOSPER CURVE was coined by Mandelbrot in 1977 in Fractals: Form, chance, and dimension. See Mathworld.

PEANO-HILBERT CURVE is found in December 1901 in the Bulletin of the American Mathematical Society. [Google print search by James A. Landau]

PEARLS OF SLUZE. Blaise Pascal (1623-1662) named the family of curves to honor Baron René François de Sluze, who studied the curves (Encyclopaedia Britannica article: "Geometry").

The PEARSON system of CURVES (describing probability distributions) was introduced by Karl Pearson in his "Contributions to the Mathematical Theory of Evolution. II. Skew Variation in Homogeneous Material," Philosophical Transactions of the Royal Society A, 186, (1895), 343-414. The curves were originally classified into Types I to IV but over the years the number of types and their definitions changed. References to "Professor Pearson’s Type III" can found in G. U. Yule "Notes on the History of Pauperism in England and Wales from 1850 ... " Journal of the Royal Statistical Society, 59, (1896), p. 324 or in Student (1908, p. 4). R. A. Fisher (1915, p. 520) refers to the "Pearson curves." [John Aldrich]

See also BETA DISTRIBUTION, CAUCHY DISTRIBUTION, and GAMMA DISTRIBUTION.

The term PEDAL CURVES is due to Olry Terquem (1782-1862) (Cajori 1919, page 228).

PELL’S EQUATION was so named by Leonhard Euler (1707-1783) in a paper of 1732-1733, even though Pell had only copied the equation from Fermat’s letters (Burton, page 504) of 1657 and 1658.

The following is taken from Sir Thomas L. Heath, Diophantus of Alexandria: A Study in the History of Greek Algebra, page 285-286:

Fermat rediscovered the problem and was the first to assert that the equation x² - Ay² = 1, where A is any integer not a square, always has an unlimited number of solutions in integers. His statement was made in a letter to Frénicle of February, 1657 (cf. Oeuvres de Fermat, II, pp. 333-4). Fermat asks Frénicle for a general rule for finding, when any number not a square is given, squares which, when they are respectively multiplied by the given number and unity is added to the product, give squares. If, says Fermat, Frénicle cannot give a general rule, will he give the smallest value of y which will satisfy the equations 61y² + 1 = x² and 109y² + 1 = x² ? ... The challenge was taken up in England by William, Viscount Brouncker, first President of the Royal Society, and Wallis. At first, owing apparently to some misunderstanding, they thought that only rational, and not necessarily integral solutions were wanted, and found of course no difficulty in solving this easy problem. Fermat was, naturally, not satisfied with this solution, and Brouncker, attacking the problem again, finally succeeded in solving it. The method is set out in letters of Wallis of 17th December, 1657, and 30th January, 1658, and in chapter XCVIII of Wallis’s Algebra; Euler also explains it fully in his Algebra (Footnote 3: Part II, chap. VII), wrongly attributing it to Pell (Footnote 4: This was the origin of the erroneous description of our equation as the "Pellian" equation. Hankel (in Zur Geschichte der Math. im Alterthum und Mittlelalter, p. 203) supposed that the equation was so called because the solution was reproduced by Pell in an English translation (1668) by Thomas Brancker of Rahn’s Algebra; but this is a misapprehension, as the so-called "Pellian" equation is not so much as mentioned in Pell’s additions (Wertheim in Bibliotheca Mathematica, III, 1902, pp. 124-6); Konen, pp. 33-4 note). The attribution of the solution to Pell as a pure mistake of Euler’s, probably due to a cursory reading by him of the second volume of Wallis’s Opera where the solution of the equation ax² + 1 = y² is given as well as information as to Pell’s work in indeterminate analysis. But Pell is not mentioned in connexion with the equation at all (Eneström in Bibliotheca Mathematica, III, 1902, p. 206).

This problem of Fermat is now known as "Pell’s equation" as a result of a mistake on the part of Euler. In some way, perhaps from a confused recollection of Wallis’s Algebra, Euler gained the mistaken impression that Wallis attributed the method of solving the problem not to Brouncker but to Pell, a contemporary of Wallis who is frequently mentioned in Wallis’s works but who appears to have had nothing to do with the solution of Fermat’s problem. Euler mentions this mistaken impression as early as 1730, when he was only 23 years old, and it is included in his definitive Introduction to Algebra written around 1770. Euler was the most widely read mathematical writer of his time, and the method from that time on has been associated with the name of Pell and the problem that it solved --- that of finding all integer solutions of y² - Ax² = 1 when A is a given number not a square --- has been known ever since as "Pell’s equation", despite the fact that it was Fermat who first indicated the importance of the problem and despite the fact that Pell had nothing whatever to do with it.

The 1910 Encyclopaedia Britannica has: "Although Pell had nothing to do with the solution, posterity has termed the equation Pell’s Equation" (OED2).

PENCIL OF LINES. Desargues coined the term ordonnance de lignes, which is translated an order of lines or a pencil of lines [James A. Landau].

PENTAGON. Pentagons are discussed in Book IV of Euclid’s Elements. The word “pentagon” appears in English in 1570 in Sir Henry Billingsley’s translation of the Elements. (OED) Earlier in 1551 in Pathway to Knowledge Robert Recorde introduced the word cinqueangle: “Defin., Figures of .v. sydes, other v. corners, which we may call cinkangles, whose sydes partlye are all equall as in A, and those are counted ruled cinkeangles” (OED). See EQUILATERAL and HEXAGON. [John Aldrich]

PENTAGRAM is found in English in 1825 in a translation of Faust. [Google print search]

The term PENTOMINO was coined by Solomon W. Golomb, who used the term in a 1953 talk to the Harvard Math Club. According to an Internet web page, the term was trademarked in 1975. (The first known pentomino problem is found in Canterbury Puzzles in 1907.)

PERCENTILE appears in 1885 in Francis Galton, ’Some results of the Anthropometric Laboratory.’s Journal of the Anthropological Institute, 14, 275-287: "The value which 50 per cent. exceeded, and 50 per cent. fell short of, is the Median Value, or the 50th per-centile, and this is practically the same as the Mean Value; its amount is 85 lbs." (p. 276) (OED2).

According to Hald (p. 604), Galton introduced the term.

PERFECT NUMBER. According to Smith (vol. 2, page 21), the Pythagoreans used this term in another sense, because apparently 10 was considered by them to be a perfect number.

Proposition 36 of Book IX of Euclid’s Elements is: "If as many numbers as we please beginning from a unit be set out continuously in double proportion, until the sum of all becomes a prime, and if the sum multiplied into the last make some number, the product will be perfect."

The Greek poet and grammarian Euphorion (born c. 275 BC?) used the phrase ". . . equal to his [or their] limbs, with the result that they are called perfect." This is an apparent reference to perfect numbers, according to J. L. Lightfoot, "An early reference to perfect numbers? Some notes on Euphorion, SH 417," Classical quarterly 48 (1998), 187-194.

The term was used by Nicomachus around A. D. 100 in Introductio Arithmetica (Burton, page 475). One translation is:

Among simple even numbers, some are superabundant, others are deficient: these two classes are as two extremes opposed to one another; as for those that occupy the middle position between the two, they are said to be perfect.

St. Augustine of Hippo (354-430) wrote De senarii numeri perfectione ("Of the perfection of the number six") in De Civitate Dei. He wrote, in translation: "Six is a number perfect in itself, and not because God created the world in six days; rather the contrary is true. God created the world in six days because this number is perfect, and it would remain perfect, even if the work of the six days did not exist."

Perfect number appears in English in 1570 in Sir Henry Billingsley’s translation of Euclid.

In 1674, Samuel Jeake wrote in Arithmetic (1696) "Perfect Numbers are almost as rare as perfect Men" (OED2).

PERFECT SETS. Georg Cantor introduced perfecte Punktmengen (perfect point-sets) in his article “Über unendliche, lineare Punktmannichfaltigkeiten 5,” Mathematische Annalen, 21 (1883), p. 576. For an account see J. W. Dauben Georg Cantor (1979, pp. 110ff). The French expression appears in a translation, Cantor’s “De la puissance des ensembles parfaits de points,” Acta Mathematica 4 (1884), 381-392. A JSTOR search found the English term perfect set in W. F. Osgood “Non-Uniform Convergence and the Integration of Series Term by Term,” American Journal of Mathematics, 19, (1897) p. 188.

This entry was contributed by John Aldrich. See also SET and SET THEORY.

PERIODOGRAM. Arthur Schuster introduced the term periodogram in "On the Investigation of Hidden Periodicities with Application to a Supposed 26 Day Period of Meteorological Phenomena," Terrestial Magnetism, 3, (1898), 13-41. He had already used the technique in his "On Lunar and Solar Periodicities of Earthquakes," Proceedings of the Royal Society, 61, (1897), 455-465 and the theory was related to his research on optics, "On Interference Phenomena," Philosophical Magazine, 37, 509-545. (David 2001)

See also HARMONIC ANALYSIS.

PERMANENT (of a square matrix). In a paper written with M. Marcus ("Permanents", Amer. Math. Monthly, 1965, p. 577) Henryk Minc, one of the great authorities in permanents, wrote:

The name "permanent" seems to have originated in Cauchy’s memoir of 1812 [B 3]. Cauchy’s "fonctions symétriques permanentes" designate any symmetric function. Some of these, however, were permanents in the sense of the definition (1.1). (...) As far as we are aware the name "permanent" as defined in (1.1) was introduced by Muir [B 38].

In his book Permanents [9] H. Minc mentions that the name permanent is essentially due to Cauchy (1812) although the word as such was first used by Muir in 1882. Nevertheless a referee of one of Minc’s earlier papers admonished him for inventing this ludicrous name!

PERMUTATION. Leibniz used the term variationes and Wallis adopted alternationes (Smith vol. 2, page 528).

In 1678 Thomas Strode, A Short Treatise of the Combinations, Elections, Permutations & Composition of Quantities, has: “By Variations, permutation or changes of the Places of Quantities, I mean, how many several ways any given Number of Quantities may be changed.” [OED]

Lexicon Technicum, or an universal English dictionary of arts and sciences (1710) has: “Variation, or Permutation of Quantities, is the changing any number of given Quantities, with respect to their Places.” [OED]

According to Smith vol. 2, page 528, permutation first appears in print with its present meaning in Ars Conjectandi by Jacques Bernoulli: "De Permutationibus. Permutationes rerum voco variationes..." This seems to be incorrect.

[Mark Thakkar contributed to this entry.]

The term PERMUTATION GROUP was coined by Galois (DSB, article: "Lagrange").

Permutation group appears in English in W. Burnside, "On the representation of a group of finite order as a permutation group, and on the composition of permutation groups," London M. S. Proc. 34.

The term PERMUTATION TEST appears in G. E. P. Box & S. L. Andersen "Permutation Theory in the Derivation of Robust Criteria and the Study of Departures from Assumption," Journal of the Royal Statistical Society. Series B, 17, (1955), p. 3. They use the term for a "remarkable new class of tests" introduced by R. A. Fisher in The Design of Experiments (1935) and quote from p. 51 of this book:  

It seems to have escaped recognition that the physical act of randomisation, which, as has been shown, is necessary for the validity of any test of significance, affords the means, in respect of any particular body of data, of examining the wider hypothesis in which no normality of distribution is implied.

(David 2001)

PERPENDICULAR was used in English by Chaucer about 1391 in A Treatise on the Astrolabe. The term is used as a geometry term in 1570 in Sir Henry Billingsley’s translation of Euclid’s Elements.

PERRON-FROBENIUS THEOREM. This result (or collection of results) is named for Oskar Perron "Zur Theorie der Matrizen" Math. Ann., 64 (1907) pp. 248-263 and Georg Frobenius "Ueber Matrizen aus nicht negativen Elementen" Sitzungsber. Königl. Preuss. Akad. Wiss. (1912) pp. 456-477.  See the entry in Encyclopedia of Mathematics.

PETERS’ FORMULA or METHOD for estimating the standard deviation of the normal distribution using absolute deviations from the mean was widely used by astronomers in the 19^th century. The method was proposed by Christian August Friedrich Peters in his “Über die Bestimmung des wahrscheinlichen Fehlers einer Beobachtung aus den Abweichungen der Beobachtungen von ihrem arithmetischen Mittel,” Astronomische Nachrichten, 44, (1856), 29-32. R. A. Fisher examined Peters’ method (mean error method) in his paper A Mathematical Examination of the Methods of Determining the Accuracy of an Observation by the Mean Error, and by the Mean Square Error (1920) and concluded that it was inferior to the mean square error method. See the entries HELMERT TRANSFORMATION, SUFFICIENCY and EFFICIENCY.

The term PFAFFIAN was introduced by Arthur Cayley, who used the term in 1852: "The permutants of this class (from their connexion with the researches of Pfaff on differential equations) I shall term ’sPfaffians’s." The term honors Johann Friedrich Pfaff (1765-1825).

PIECEWISE is found in 1933 in the phrase "vectors which are only piecewise differentiable" in Vector Analysis by H. B. Phillips (OED2).

The name PIE CHART is found in 1922 in A. C. Haskell, Graphic Charts in Business (OED2). Pie charts only became common in the 20^th century but they seem to have been first used by William Playfair in 1801. See that date in Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization 1800-1849.

PIGEONHOLE PRINCIPLE. The principle itself is attributed to Dirichlet in 1834, although he apparently used the term Schubfachprinzip.

In Dirichlet’s Vorlesungen über Zahlentheorie (Lectures on Number Theory, prepared for publication by Dedekind, first edition 1863), the argument is used in connection with Pell’s equation but it bears no specific name [Peter Flor, Gunnar Berg].

In 1905 in Bachmann’s "Zahlentheorie," part 5, the principle is stated as a "very simple fact" on which Dirichlet is said to have based his theory of units in number fields; no name is attached to the principle [Peter Flor].

In 1910 in Geometrie der Zahlen, Minkowski calls it "a famous method of Dirichlet" [Peter Flor].

According to Peter Flor, "the term Schubfachschluss, with or without a reference to Dirichlet, was used widely by German speaking number theorists at the universities of Vienna and Hamburg when I studied there in the 1950s. It occurs, among others, in the number theory books by Hasse and by Aigner."

In Swedish, the principle is called (in translation) "Dirichlets box principle" [Gunnar Berg]. The French term is "le principe des tiroirs de Dirichlet," which can be translated "the principle of the drawers of Dirichlet." In Portuguese, the term is "principio da casa dos pombos" (lit. principle of the house of the pigeons) or "das gavetas de Dirichlet" (lit. of the drawers of Dirichlet) [Julio González Cabillón].

Pigeonhole principle occurs in English in Raphael M. Robinson’s paper "On the Simultaneous Approximation of Two Real Numbers," presented to the American Mathematical Society on November 23, 1940, and published in the Bulletin of the Society in 1941. Cf. volume 47, pp 512-513. In a footnote to this article, Robinson states:

The method used in this proof (Schubfachprinzip or "pigeonhole principle") was first used by Dirichlet in connection with a similar problem. We sketch the proof here in order to compare it with the proof of the theorem below, which also uses that method.

Paul Erdös referred to Dedekind’s pigeon-hole principle in "Combinatorial Problems in Set Theory," an address he delivered in 1953 before the AMS [Julio González Cabillón].

Pigeon-hole principle occurs in English in Paul Erdös and R. Rado, "A partition calculus in set theory," Bull. Am. Math. Soc. 62 (Sept. 1956):

Dedekind’s pigeon-hole principle, also known as the box argument or the chest of drawers argument (Schubfachprinzip) can be described, rather vaguely, as follows. If sufficiently many objects are distributed over not too many classes, then at least one class contains many of these objects.

Dirichlet’s pigeon-hole principle (chest-of-drawers principle, Schubfachprinzip) asserts, roughly, that if a large number of objects is distributed in any way over not too many classes, then one of these classes contains many of these objects.

PIVOTAL in Statistics. The term was introduced by R. A. Fisher in his "The Asymptotic Approach to Behrens’s Integral, with Further Tables for the d Test of Significance", Annals of Eugenics, 11, (1941), 141-172. Fisher wrote, "In Student’s test the quantity t appears in two roles. First, it is the pivotal quantity the distribution of which is independent of the population sampled, and the distribution of which is therefore accepted for the particular sample under consideration ... Secondly it is the quantity tabulated." (p. 147) Fisher only used the term "pivotal" when expounding the fiducial argument but now the term is used more widely. [John Aldrich, based on information in David (2001)].

PLACE VALUE appears in 1847 in A Treatise on Algebra, Containing the Latest Improvements. Adapted to the Use of Schools and Colleges Charles William Hackley: "It is clear from this, that if we add the figures of the number without regarding their place value, the sum obtained and the proposed number will have the same minimum residue." [Google print search]

The word PLAGIOGRAPH was coined by James Joseph Sylvester (DSB).

PLANE GEOMETRY appears in English in a letter from John Collins to Oldenburg for Tschirnhaus written in May 1676: "...Mechanicall tentative Constructions performed by Plaine Geometry are much to be preferred..." [James A. Landau].

PLATONIC SOLIDS. The five regular polyhedra are discussed by Plato in the Timaeus where they provide the basis for a theory of the universe. Their earlier history is obscure: William C. Waterhouse writes in “The Discovery of the Regular Solids” Archive for History of Exact Science, 9, (1972-1973)

The history of the regular solids thus rests almost entirely on a scholium to Euclid which reads as follows: “In this book, the 13th, are constructed the 5 figures called Platonic, which however do not belong to Plato. Three of these 5 figures, the cube, pyramid, and dodecahedron, belong to the Pythagoreans; while the octahedron and icosahedron belong to Theaetetus.”

This citation was provided by Paul Bien. The five solids are the subject of Book XIII of Euclid’s Elements.

In English, the OED shows a use of Platonicall bodies in 1571 by Thomas Digges and a Google books search found a use of Platonic solids in 1787 in The young geometrician’s companion: being a new and comprehensive course of practical geometry by the Reverend Richard Turner.

See the entries CUBE, POLYHEDRON and PYRAMID.

PLATONISM. In the specific sense now widely used in discussions on the foundations of mathematics, this term was introduced by Paul Bernays (1888-1977) in Sur lê platonisme dans les mathematiques, Einseignement Math., 34 (1935-1936), 52-69. We quote the relevant passage:

If we compare Hilbert’s axiom system to Euclid’s (...), we notice that Euclid speaks of figures to be constructed, whereas, for Hilbert, systems of points, straight lines, and planes exist from the outset. (...) This example shows already that the tendency (...) consists in viewing the objects as cut off from all links with the reflecting subject. Since this tendency asserted itself especially in the philosophy of Plato, allow me to call it "platonism".

PLETHYSM. According to Richard P. Stanley in Enumerative Combinatorics, the term was introduced in D. E. Littlewood, “Invariant theory, tensors and group characters,” Philos. Trans. Roy. Soc. London. Ser. A. 239, (1944), 305–365. The term was suggested to Littlewood by M. L. Clark after the Greek word plethysmos (“multiplication” in modern Greek). [Information from this web page.]

PLUQUATERNION was coined by Thomas Kirkman (1806-1895), as he attempted to extend further the notion of quaternions.

PLUS and MINUS. From the OED2:

The quasi-prepositional use (sense I), from which all the other English uses have been developed, did not exist in Latin of any period. It probably originated in the commercial langauge of the Middle Ages. In Germany, and perhaps in other countries, the Latin words plus and minus were used by merchants to mark an excess or deficiency in weight or measure, the amount of which was appended in figures. The earliest known examples of the modern sense of minus are German, of about the same date as our oldest quotation. ... In a somewhat different sense, plus and minus had been employed in 1202 by Leonardo of Pisa for the excess and deficiency in the results of the two suppositions in the Rule of Double Position; and an Italian writer of the 14th century used meno to indicate the subtraction of a number to which it was prefixed.

PLUS OR MINUS. The expression "plus or minus" is very old, having been in common use by the Romans to indicate simply "more or less" (Smith vol. 2, page 402).

PLUS OR MINUS SIGN. In 1801 Mathematics by Thomas & Andrews has: "The double or ambiguous sign ± signifies plus or minus the quantity, which immediately follows it, and being placed between two quantities, it denotes their sum, or difference." [Google print search]

The symbol ± is called the ambiguous sign in 1811 in An Elementary Investigation of the Theory of Numbers by Peter Barlow [James A. Landau].

PLUS SIGN. Positive sign is found in 1704 in Lexicon Technicum.

Affirmative sign is found in 1752 in The Elements of Algebra: In a New and Easy Method by Nathaniel Hammond. [Google print search]

Plus sign is found in 1835 in Key to professor Young’s Algebra by W. H. Spiller and John Radford Young. [Google print search]

POINT. Definition 1 in the first book of Euclid’s Elements states “A point is that which has no part.” In the notes to his edition of the Elements T. L Heath (1926, vol. 1, pp. 155-6) describes how sêmeion, the term used by Euclid and which elsewhere signified a punctuation mark, replaced stigmê, meaning a puncture. Euclid’s Latin translators used punctum. Thus Capella (c. 460) translated Euclid’s definition as “Punctum est cuius pars nihil est.” (Quoted by Smith vol. 2, p. 274.)

The word appears in English in this sense in John Trevisa’s translation (a1398) of the encyclopaedia De Proprietatibus Rerum which was written about 1245 by Bartholomaeus Anglicus. The quotation in the OED is, “þe lyne..bigynneþ at a poynt and endeþ at a poynt.” Trevisa’s translation was one of the first books to be printed in English (around 1495). The work in its final form (of 1582) has been called “Shakespeare’s encyclopaedia.”

In the nineteenth and early twentieth centuries the concept of space was broadened to accommodate non-euclidean geometries and abstract spaces—see the entry SPACE. Elements of these new spaces were called points. Thus Hausdorff introduces a topological space with the words “Unter einem topologischen Raum verstehen wir einen Menge E, worin den Elementen (Punkten) [a set E, where the elements (points)]...” Grundzüge der Mengenlehre (1914, p. 213).

POINTLESS (geometry or topology). Forms of geometry (topology) that do not use the point as a primitive concept are called “pointless” or “point-free” or “without points.” Such structures have a long history and titles include “Topology without Points” by K. Menger, Rice Institute Pamphlets, 27, (1940), 80-107 and, perhaps inevitably, “The Point of Pointless Topology” by P. T. Johnstone, Bulletin of the American Mathematical Society, 8, (1983), 41-53.

POINT OF ACCUMULATION. See limit point.

The term POINT-SERIES GEOMETRY was coined by E. A. Weiss [DSB, article: "Reye"].

POINT-SET. The term was introduced in German by Georg Cantor. At first Cantor used the term Punktmannichfaltigkeit; see e.g. his “Über unendliche, lineare Punktmannichfaltigkeiten, (Part 1) Mathematische Annalen, 15 (1879), 1-7. He then changed to Punktmenge; see e.g. his “Über verschiedene Theoreme aus der Theorie der Punktmengen in einem n-fach ausgedehnten stetigen Raume,” Acta Mathematica, 7, (1885) 105-124.

The English term is used in E. H. Moore “Concerning Harnack’s Theory of Improper Definite Integrals,” Transactions of the American Mathematical Society, 2, (1901), p. 297. See SET and SET THEORY.

The term POINT-SET TOPOLOGY was coined by Robert Lee Moore (1882-1974), according to the University of St. Andrews website. Moore’s Foundations of point set topology was published in 1932.

POINT-SLOPE FORM. Slope-point form is found in 1904 in Elements of the Differential and Integral Calculus by William Anthony Granville [James A. Landau].

Point-slope form is found in 1904 in The Elements of Analytic Geometry by Percey Franklyn Smith and Arthur Sullivan Gale. [Google print search]

See slope on Earliest Uses of Symbols from Geometry.

POISSON DISTRIBUTION. S. D. Poisson’s result on the limiting form of the binomial appears in the Mémoire sur la proportion des naissances des filles et des garcons (1830, pp. 261-2) and is reproduced in the Recherchés sur la probabilité des jugements en matière criminelle et matière civil (1837, pp. 205ff). Poisson’s ‘ownership’ of this distribution has been debated for De Moivre had come very close to it in 1712 (Hald (1990, p. 214)) and Poisson "does not discuss the properties and applications of this distribution" (Hald (1998, p. 571)). L. J. Bortkiewicz discussed both in his tract Das Gesetz der kleinen Zahlen (1898); this has the famous example of cavalrymen being killed by the kick of a horse. 

In Britain the distribution was not well known at the beginning of the 20^th century--Student actually rediscovered it in his "On the Error of Counting with a Haemacytometer," Biometrika, 5, (1907), 351-360. However Poisson received full attention in two papers published in 1914: Lucy Whitaker’s "On the Poisson Law of Small Numbers," Biometrika, 10, 36-71 and Herbert Edward Soper’s "Tables of Poisson’s Exponential Binomial Limit" Biometrika, 10, 25-35  Whitaker called the distribution the Poisson-exponential, while Soper referred to Poisson’s exponential binomial limit or Poisson’s exponential series.

Poisson distribution appears in 1922 in R. A. Fisher, H.G. Thornton and W.A. Mackenzie The Accuracy of the Plating Method of Estimating the Density of Bacterial Populations, p. 331: "When the statistical examination of these data was commenced it was not anticipated that any clear relationship with the Poisson distribution would be obtained" (OED2). Fisher’s Statistical Methods for Research Workers (1925, section 15) established Poisson as ‘core repertory.’

[This entry was contributed by John Aldrich, based on Hald (1990 and -98) David (1995).]

POLAR COORDINATES. According to Daniel L. Klaasen in Historical Topics for the Mathematical Classroom:

Isaac Newton was the first to think of using polar coordinates. In a treatise Method of Fluxions (written about 1671), which dealt with curves defined analytically, Newton showed ten types of coordinate systems that could be used; one of these ten was the system of polar coordinates. However, this work by Newton was not published until 1736; in 1691 Jakob Bernoulli derived and made public the concept of polar coordinates in the Acta eruditorum. The polar system used for reference a point on a line rather than two intersecting lines. The line was called the "polar axis," and the point on the line was called the "pole." The position of any point in a plane was then described first by the length of a vector from the pole to the point and second by the angle the vector made with the polar axis.

Polar co-ordinates is found in English in 1816 in a translation of Lacroix’s Differential and Integral Calculus: "The variables in this equation are what Geometers have called polar co-ordinates" (OED2).

POLE and POLAR. The term pôle (in projective geometry) was introduced by François Joseph Servois (1768-1847) in 1811 (Smith vol. 2, page 334). It was introduced in his first contribution to Gergonne’s Annales de mathématiques pures et appliquées (DSB).

The term polar (polaire) was introduced by Joseph-Diez Gergonne in its modern geometric sense in 1813 (Smith vol. II, page 334).

The term POLAR (with respect to a triangle) was coined by Arthur Cayley. The term is found in Cayley "Sur quelques théorèmes de la géométrie de position," Crelle’s journal 34 (1847) 270-275, or Cayley’s collected mathematical papers Vol. 1 # 55, pp. 356-361: " ...seront situés (comme on le sait) sur une même droite, qui est celle que je nomme polaire de O, relative aux côtés du triangle, et que M. Plücker a nommé "harmonicale." [Ken Pledger]

The term POLE (in complex analysis) appears in Briot & Bouquet’s Théorie des fonctions elliptiques (1859, p. 15). The concept was used by Cauchy but the term was not. (Grattan-Guinness (1997, p. 388). See the Mathworld entry.

POLISH SPACE (espace polonaise) was defined in Nicolas Bourbaki, Topologie Generale Chapitre IX, deuzième édition 1958 [Stacy Langton]. See the Wikipedia article.

PÓLYA or PÓLYA-EGGENBERGER DISTRIBUTION, FORMULA, URN MODEL etc. are terms associated with the paper by George Pólya and F. Eggenberger “Uber die Statistik verketteter Vorgänge,” Zeitschrift fur Angewandte Mathematik und Mechanik 3 (1923), 279-89. (Reprinted in George Pólya Collected Papers Volume IV.) The term “Pólya-Eggenberger distribution” appears in W. Feller “On a General Class of “Contagious” Distributions,” Annals of Mathematical Statistics, 14, (1943), 389-400. [John Aldrich]

POLYGON was used in classical Greek. Euclid, however, preferred "polypleuron," designating many sides rather than many vertices.

Polygon appears in English in 1570 in Sir Henry Billingsley’s translation of Euclid, folio 125. In an addition after Euclid IV.16, which Billingsley ascribes to Flussates (François de Foix, Bishop of Aire), he mentions "Poligonon figures;" and in a marginal note explains "A Poligonon figure is a figure consisting of many sides." [Ken Pledger]

In 1571 in A Geometricall Practise, named Pantometria, Thomas Digges (d. 1595) wrote, "Polygona are such Figures as haue moe than foure sides" (OED2).

Multangle is found in 1674 in Samuel Jeake, Arith. (1696): "If 3 [angles] then called a Triangle, if 4 a Quadrangle, if more a Multangle or Polygone" (OED2).

In 1768-1771 the first edition of the Encyclopaedia Britannica has: "Every other right lined figure, that has more sides than four, is in general called a polygon."

In the 1828 Webster dictionary, the definition of polygon is: "In geometry, a figure of many angles and sides, and whose perimeter consists at least of more than four sides." In this dictionary, the word polygon appears in the definition of the enneagon (nine sides) and the dodecagon, but not in the definitions of figures consisting of fewer than nine sides.

In 1828, Elements of Geometry and Trigonometry (1832) by David Brewster (a translation of Legendre) has: "Regular polygons may have any number of sides: the equilateral triangle is one of three sides; the square is one of four."

POLYGONAL NUMBER and FIGURATE NUMBER. Pythagoras was acquainted at least with the triangular numbers, and very probably with square numbers, and the other polygonal numbers were treated by later members of his school (Burton, page 102).

According to Diophantus, Hypsicles (c. 190 BC-120 BC) defined polygonal numbers.

Nicomachus discussed polygonal numbers in the Introductio.

A tract on polygonal numbers attributed to Diophantus exists in fragmentary form.

Boethius defined figurate numbers as numbers "qui circa figuras geometricas et earum spatia demensionesque versantur" (Smith vol. 2, page 24).

In 1646 Vieta (1540-1603) referred to triangular and pyramidal numbers: "In prima adfectione per unitatis crementum, in secunda per numeros triangulos, in tertia per numeros pyramidales, in quarta per numeros triangulo-triangulos, in quinta per numeros triangulo-pyramidales."

In 1665 Pascal wrote his Treatise on Figurative Numbers.

Pentagonal number appears in English in 1670 in Collins in Rigaud Corr. Sci. Men (1841): "It is likewise a pentagonal number, or composed of two, three, four, or five pentagonal numbers" (OED2).

Pyramidal number appears in English in 1674 in Samuel Jeake’s Arithmetic: "Six is called the first Pyramidal Number; for the Units therein may be so placed, as to represent a Pyramis" (OED2).

Polygonal number is found in English in 1704 in Lexicon Technicum: "Polygonal Numbers, are such as are the Sums or Aggregates of Series of Numbers in Arithmetical Progression, beginning with Unity; and so placed, that they represent the Form of a Polygon" (OED2).

Figurate number and triangular (as a noun) appear in English in 1706 in William Jones, Synopsis palmariorum matheseos: "The Sums of Numbers in a Continued Arithmetic Proportion from Unity are call’sd Figurate ... Numbers. ... In a Rank of Triangulars their Sums are called Triangulars or Figurates of the 3d Order" (OED2).

Triangular number appears in English in 1796 in Hutton’s Math. Dict.: "The triangular numbers 1, 3, 6, 10, 15, &c" (OED2).

In 1811 Peter Barlow used multangular numbers in An Elementary Investigation of the Theory of Numbers [James A. Landau].

POLYHEDRON. According to Ken Pledger, polyhedron was used by Euclid without a proper definition, just as he used "parallelogram." In I.33 he constructs a parallelogram without naming it; and in I.34 he first refers to a "parallelogrammic (parallel-lined) area," then in the proof shortens it to "parallelogram." In a similar way, XII.17 uses "polyhedron" as a descriptive expression for a solid with many faces, then more or less adopts it as a technical term.

However, according to Smith (vol. 2, page 295), "The word ’spolyhedron’s is not found in the Elements of Euclid; he uses ’solid,’s ’soctahedron,’s and ’sdodecahedron,’s but does not mention the general solid bounded by planes."

In English, polyhedron is found in 1570 in Sir Henry Billingsley’s translation of Euclid XII.17. Early in the proof (folio 377) Billingsley amplifies it to "...a Polyhedron, or a solide of many sides,..." [Ken Pledger].

In English, in the 17th through 19th centuries, the word is often spelled polyedron.

POLYNOMIAL was used by François Viéta (1540-1603) (Cajori 1919, page 139).

The word is found in English in 1674 in Arithmetic by Samuel Jeake (1623-1690): "Those knit together by both Signs are called...by some Multinomials, or Polynomials, that is, many named" (OED2). [According to An Etymological Dictionary of the English Language (1879-1882), by Rev. Walter Skeat, polynomial is "an ill-formed word, due to the use of binomial. It should rather have been polynominal, and even then would be a hybrid word."]

The term POLYOMINO was coined by Solomon W. Golomb in 1954 (Schwartzman, p. 169).

The term POLYSTAR was coined by Richard L. Francis in 1988 (Schwartzman, p. 169).

The English word appears in Alicia Boole Stott “Geometrical Deduction of Semiregular from Regular Polytopes and Space Fillings,” Verhandelingen der Koninklijke Akademie van Wetenschappen te Amsterdam, 11, (1910), 3–24. See Irene Polo-Blanco “Alicia Boole Stott, a Geometer in Higher Dimension,” Historia Mathematica, 35, (2008), 123-139.

PONS ASINORUM usually refers to Proposition 5 of Book I of Euclid. From Smith vol. 2, page 284:

The proposition represented substantially the limit of instruction in many courses in the Middle Ages. It formed a bridge across which fools could not hope to pass, and was therefore known as the pons asinorum, or bridge of fools. It has also been suggested that the figure given by Euclid resembles the simplest form of a truss bridge, one that even a fool could make. The name seems to be medieval.

The proposition was also called elefuga, a term which Roger Bacon (c. 1250) explains as meaning the flight of the miserable ones, because at this point they usually abandoned geometry (Smith vol. 2, page 284).

Pons asinorum is found in English in 1751 in Smollett, Per. Pic.: "Peregrine..began to read Euclid..but he had scarce advanced beyond the Pons Asinorum, when his ardor abated" (OED2).

According to Smith, pons asinorum has also been used to refer to the Pythagorean theorem.

POPULATION and SAMPLE have been linked technical terms in statistics since the turn of the 20^th century. In the 19^th century population came to be applied to animals and plants and sample, which was primarily a commercial term came, to be applied to objects of scientific interest; the OED quotes T. H. Huxley writing in 1878 (Physiography, xvi. 2), "numerous samples of the sea bottom were secured." The terms were brought into statistics by people interested in the statistical analysis of biological populations.

Population and sample acquired a statistical colouring in the work of Francis Galton and W. F. R. Weldon. In "Typical laws of heredity," Nature, 15, (1877), April 19^th, p. 532 Galton wrote, "the population ... will conform to the law of deviation [the normal distribution]." Weldon applied statistical methods to "samples" of crabs in On Certain Correlated Variations in Carcinus moenas, Proceedings of the Royal Society, 54, (1893), 318-329.

The third founder of biometry, Karl Pearson, further abstracted the terms, brought them together and established the population-sample terminology in theoretical statistics. In "On the Probable Errors of Frequency Constants," Biometrika, 2, (1903) p. 273 he wrote, "If the whole of a population were taken we should have certain values for its statistical constants, but in actual practice we are only able to take a sample ...."

It soon became clear that the population of theoretical statistics was a much more complex concept than the population of a country. In his "The Probable Error of a Mean", Biometrika, 6, (1908), pp. 1-25 Student considered a "normal population" from which "random samples" are drawn. In another paper, "Probable Error of a Correlation Coefficient," (Biometrika, 6, (1908), p. 302), Student explained that the "indefinitely large population [from which the random sample is obtained] need not actually exist," i.e. it may exist only in imagination. R. A. Fisher used the phrase "hypothetical infinite population" in "On the Mathematical Foundations of Theoretical Statistics", (Philosophical Transactions of the Royal Society of London, Ser. A, 222, (1922), p. 311) and "infinite hypothetical population" in "Theory of Statistical Estimation.," Proceedings of the Cambridge Philosophical Society, 22, (1925), 700-725. His prefatory note to the latter (p. 700) tries to clarify what he meant by such a thing.

Although Student (1908) had used the phrases, "mean of the population" and "mean of the sample," it was not until the 1930s that such terms as sample mean or population standard deviation became prominent. The new sensitivity to the population-sample distinction was largely a response to Fisher’s complaint that statisticians had not properly distinguished population and sample quantities, a complaint that led him to introduce the terms parameter and statistic.

This entry was contributed by John Aldrich. See BIOMETRY, PARAMETER and RANDOM SAMPLE.

POSET, an abbreviation of "partially ordered set", is due to Garret Birkhoff (1911-1996), as said by himself in the second edition (1948, p. 1) of his book Lattice Theory. The term is now firmly established [Carlos César de Araújo].

POSITIONAL NOTATION is found in 1890 in The Theory of Determinants: In the Historical Order of Development by Thomas Muir: "Taking this up in order, we observe that Vandermonde proposes for coefficients a positional notation essentially the same as that of Leibnitz, writing 1₂ where Leibnitz wrote 12 or 1₂." [Google print search]

Positional notation is also found in "Our Symbol for Zero" by George Bruce Halsted in American Mathematical Monthly, Vol. 10, No. 4. (Apr., 1903), pp. 89-90 [JSTOR].

POSITIVE. In the 15th century the names "positive" and "affirmative" were used to indicate positive numbers (Smith vol. 2, page 259).

In 1544 in Arithmetica integra Stifel called positive numbers numeri veri (Smith vol. 2, page 260).

Cardano (1545) called positive numbers numeri veri or veri numeri (Smith vol. 2, page 259).

Napier (c. 1600) used the adjective abundantes to designate positive numbers (Smith vol. 2, page 260).

The OED shows a use of affirmative to mean positive in 1693 by E. Halley, "Algebra" in Phil. Trans. XVII: "Which is affirmative when 2rq is less than dr - dq, otherwise negative."

Positive is found in English in the phrase "the Affirmative or Positive Sign +" in 1704 in Lexicon technicum, or an universal English dictionary of arts and sciences by John Harris.

In the French language, zero is a positive number. Trésor de la Langue Française has "Nombre positif. Nombre réel égal ou supèrieur à zéro ..." [William C. Waterhouse].

POSITIVE DEFINITE appears in 1905 in volume I of The Theory of Functions of Real Variables by James Pierpont [James A. Landau].

POSTERIOR PROBABILITY and PRIOR PROBABILITY.  Jakob Bernoulli used the terms a priori and a posteriori to distinguish two ways of deriving probabilities: deduction a priori (without experience) is possible when there are specially constructed devices, like dice but otherwise, "what you cannot deduce a priori, you can at least deduce a posteriori--i.e., you will be able to make a deduction from many observed outcomes of similar events." (Ars Conjectandi (1713) Part IV, Chapter 4.) Cournot uses the term in this sense in Chapter VIII, "Des probabilités à posteriori," of his Exposition de la Théorie des Chances et des Probabilités.

In the course of the 19^th century "a priori probability" and "a posteriori probability" became the standard terms in stating the theorem now called after Bayes. Although Bayes’s theorem (the theorem on the probability of causes, the theorem on inverse probability) had an established place in expositions of probability from Laplace’s Théorie Analytique des Probabilités, (1812) onwards, it took some decades for the terminology to become standardised.

In the English literature W. Lubbock & J. E. Drinkwater-Bethune (On Probability, 1830, p. 25) referred to "the probability [of the hypothesis] antecedent to the observations under consideration" as its "à priori probability." W. F. Donkin added the term "a posteriori probability" ("On Certain Questions Relating to the Theory of Probabilities," Philosophical Magazine, 1, (1851), 353-368). By 1866 Isaac Todhunter was writing in his widely-used textbook, Algebra for the Use of Colleges and Schools (p. 456), that "a priori probability" and "a posteriori probability" are the "usual" terms. Todhunter (following Donkin) wrote the formula as

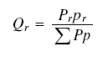
where P_r is "the probability of the hypothesis of the r^th cause" (a priori probability), p_r is "the probability of the event on the hypothesis of the r^th cause" and  Q_r is "the probability of the hypothesis of the r^th cause estimated after the event" (a posteriori probability). There was no standard term for p_r until Harold Jeffreys adopted R. A. Fisher’s term "likelihood" in the 1930s. Nor was there a standard term (or symbol) for conditional probability.

The contractions posterior probability and prior probability were introduced by Dorothy Wrinch and Harold Jeffreys "On Certain Fundamental Principles of Scientific Inquiry," Philosophical Magazine, 42, (1921), 369-390.

Howard Raiffa and Robert Schlaifer introduced the term preposterior, "choice of a terminal act after an experiment has already been performed ... we call terminal analysis, and choice of the experiment which is to be performed ... we call preposterior analysis." (Applied Statistical Decision Theory (1961) p. x.)

This entry was contributed by John Aldrich, using David (2001) and Hald (1998, p. 162). See also BAYES, CONDITIONAL PROBABILITY, INVERSE PROBABILITY and LIKELIHOOD.

POSTFIX NOTATION is found in R. M. Graham, "Bounded Context Translation," Proceedings of the Eastern Joint Computer Conference, AFIPS, 25 (1964) [James A. Landau].

POSTULATE appears in the early translations of Euclid’s Elements and was commonly used by the medieval Latin writers (Smith vol. 2, page 280). The Greek original was .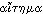

The most debated of the postulates, the parallel postulate, is postulate 5. In the notes to his edition of the Elements T. L Heath (1926, vol. 1, p. 202) writes, "From the very beginning ... the Postulate was attacked as such and attempts were made to prove it as a theorem or to get rid of it by adopting some other definition of parallels."

In English, postulate is found in 1646 in Pseudodoxia epidemica or enquiries into very many received tenents by Sir Thomas Browne in the phrase "the postulate of Euclide" (OED2).

See AXIOM.

POTENTIAL FUNCTION. This term was used by Daniel Bernoulli in 1738 in Hydrodynamica (Kline, page 524).

According to Smith (1906) and the Encyclopaedia Britannica (article: "Green"), the term potential function was introduced by George Green (1793-1841) in 1828 in Essay on the Application of Mathematical Analysis to the Theory of Electricity and Magnetism: "Nearly all the attractive and repulsive forces..in nature are such, that if we consider any material point p, the effect, in a given direction, of all the forces acting upon that point, arising from any system of bodies S under consideration, will be expressed by a partial differential of a certain function of the co ordinates which serve to define the point’s position in space. The consideration of this function is of great importance in many inquiries... We shall often have occasion to speak of this function, and will therefore, for abridgement, call it the potential function arising from the system S." ( Green’s Papers, p. 9)

POTENTIAL as the name of a function was introduced by Gauss in 1840, according to G. F. Becker in Amer. Jrnl. Sci. 1893, Feb. 97. [Cf. Gauss Allgem. Lehrsätze d. Quadrats d. Entfernung Wks. 1877 V. 200: "Zur bequemern Handhabung..werden wir uns erlauben dieses V mit einer besonderen Benennung zu belegen, und die Grösse das Potential der Massen, worauf sie sich bezieht, nennen."]

POWER appears in English in 1570 in Sir Henry Billingsley’s translation of Euclid’s Elements: "The power of a line, is the square of the same line."

POWER (meaning the cardinal number of a set) was coined by Georg Cantor (1845-1918) (Katz, page 734). Cantor used the German word Machtigkeit. See p. 481 of his " Beiträge zur Begründung der transfiniten Mengelehre" [Contributions to the founding of the theory of transfinite numbers], Mathematische Annalen, 46, (1895), 481-512.

POWER (of a test) is found in 1933 in J. Neyman and E. S. Pearson, "The Testing of Statistical Hypotheses in Relation to Probabilities A Priori," Proceedings of the Cambridge Philosophical Society, 24, 492-510. "The probability of rejecting the hypothesis tested, H₀, when the true hypothesis is H_i, or P(w| H_i), may be termed the power of the critical region w with respect to H_i." The concept of a test being more powerful than another is introduced in the same paper, as is the concept of a uniformly more powerful test.

The term uniformly most powerful test (with a result on the existence of such tests) appears in R. A. Fisher, "Two New Properties of Mathematical Likelihood", Proceedings of the Royal Society, Series A, vol. 144 (1934) p. 295  [James A. Landau]. Fisher had not yet started criticising Neyman and Pearson, beyond insisting that their "interesting new line of approach" would benefit if they paid more attention to his theory of estimation.

Power function appears in J. Neyman and E. S. Pearson’s "Contributions to the Theory of Testing Statistical Hypotheses," Statistical Research Memoirs, 1, (1936), 1-37. (David 2001.)

See also HYPOTHESIS AND HYPOTHESIS TESTING.

The expression POWER OF A POINT WITH RESPECT TO A CIRCLE was coined (in German) by Jacob Steiner [Julio González Cabillón].

POWER SERIES is found in English in 1893 in Theory of Functions of Complex Variable by A. R. Forsyth: "Any one of the continuations of a uniform function, represented by a power-series, can be derived from any other" (OED2).

PRECALCULUS is found in 1947 in Mary Draper Boeker, The Status of the Beginning Calculus Students in Pre-Calculus College Mathematics, Bureau of Publications, Teachers College, Columbia University.

Precalculus is found as a noun on Dec. 1, 1968, in the Sunday Gazette-Mail of Charleston, W. Va.: “Although he is chairman of the department, Dr. [James C.] Eaves is now teaching precalculus to about 125 freshmen, and he reportedly knows each by name.”

PREDICATE CALCULUS. The OED refers to D. Hilbert & R. Ackermann Grundzüge der theoretischen Logik (1928) ii. p. 34 for prädikatenkalkül. A JSTOR search found the English term in 1939 in Laszlo Kalmar "On the Reduction of the Decision Problem. First Paper. Ackermann Prefix, A Single Binary Predicate," Journal of Symbolic Logic, 4, (1939), p. 7.

PREFIX (notation) is found in S. Gorn, "An axiomatic approach to prefix languages," Symbol. Languages in Data Processing, Proc. Sympos., March. 26-31, 1962, 1-21 (1962).

PRENEX NORMAL FORM. According to Webster’s Third New International Dictionary, the word comes from Late Latin praenexus (tied up or bound in front), from Latin prae- pre- + nexus, (past participle of nectere to tie, bind).

A JSTOR search finds "the equivalent prenex form" in Lazlo Kalmar, "On the Reduction of the Decision Problem. First Paper. Ackermann Prefix, A Single Binary Predicate," The Journal of Symbolic Logic, March 1939.

Prenex normal form is found in 1944 in A. Church, Ann. Math. Stud. xiii. 60 (OED2).

PRESENT VALUE appears in Edmund Halley, "An Estimate of the Degrees of the Mortality of Mankind," Philosophical Transactions of the Royal Society, XVII (1693) [James A. Landau].

PRE-WHITENING occurs in G. Hext, "A note on pre-whitening and recolouring," Stanford Univ. Dept. Statist. Tech. Rep no. 13 (1964) [James A. Landau]. The term was probably first used in B. Blackman & J. W. Tukey’s "The Measurement of Power Spectra," Bell System Technical Journal, 37, (1958).

PRIMALITY is is found in 1919 in Dickson: "T. E. Mason described a mechanical device for applying Lucas’s method for testing the primality of 2^4q+3 - 1."

PRIME NUMBER. Iamblichus writes that Thymaridas called a prime number rectilinear since it can only be represented one-dimensionally.

In English prime number is found in Sir Henry Billingsley’s 1570 translation of Euclid’s Elements (OED2).

Some older textbooks include 1 as a prime number.

In his Algebra (1770), Euler did not consider 1 a prime [William C. Waterhouse].

In 1859, Lebesgue stated explicitly that 1 is prime in Exercices d’sanalyse numérique [Udai Venedem].

In 1866, Primary Elements of Algebra for Common Schools and Academies by Joseph Ray has:

All numbers are either prime or composite; and every composite number is the product of two or more prime numbers. The prime numbers are 1, 2, 3, 5, 7, 11, 13, 17, etc. The composite numbers are 4, 6, 8, 9, 10, 12, 14, 15, 16, etc.

Numbers which cannot be produced by multiplying together two or more numbers, each of which is greater than a unit, are called prime numbers.

A number that has no exact divisor except itself and 1 is called a Prime Number. Thus, 1, 3, 5, 7, 11, 13, etc. are prime numbers.

[James A. Landau provided some of the above citations.]

PRIME NUMBER THEOREM. The theorem was proved independently by Hadamard and de la Vallée Poussin in 1896. Edmund Landau called it der Primzahlsatz, for brevity and in recognition of the theorem’s importance: see Handbuch der Lehre von der Verteilung der Primzahlen (1909, Erster Band, p. vii.) See also Cajori 1919, page 439. The term was quickly translated into English: see the 1915 quotation from Ramanujan in the entry DEEP THEOREM. For further information see Mathworld: PrimeNumberTheorem. [John Aldrich]

PRIMITIVE (in group theory). The German word primitiv appears in Sophus Lie, Theorie der Transformationsgruppen (1888).

Primitive appears in J. M. Page’s exposition of Lie’s theory, “On the Primitive Groups of Transformations in Space of Four Dimensions,” American Journal of Mathematics 10, (1888), 293-346. Page writes: “A group in the plane is primitive when with each ordinary point which we hold, no invariant direction is connected.” (OED). [John Aldrich]

PRIMITIVE FUNCTION. In Theory of Analytic Functions (Théorie des fonctions analytiques 1797), Joseph Lagrange wrote, in translation:

Let us assign to the variable of a function some increment by adding to this variable an arbitrary quantity; we can, if the function is algebraic, expand it in terms of the powers of this quantity by using the familiar rules of algebra. The first term of the expansion will be the given function, which will be called the primitive function; the following terms will be formed of various functions of the same variable multiplied by the successive powers of the arbitrary quantity. These new functions will depend only on the primitive function from which they are derived and may be called the derivative functions.

The preceding was taken from Struik, A Source Book in Mathematics, p. 388. [Citation provided by Dave L. Renfro]

Lacroix used fonction primitive in Traité du calcul différentiel et integral (1797-1800). The term appears in English in the 1816 translation of this work.

See DIFFERENTIAL CALCULUS.

PRIMITIVE RECURSIVE FUNCTION was coined by Rózsa Péter (1905-1977) in “Über den Zusammenhang der verschiedenen Begriffe der rekursiven Funktion,” Mathematische Annalen, 110, (1934), 612-632.

The English term appeared in S. C. Kleene “General Recursive Functions of Natural Numbers,” Mathematische Annalen, 112, (1936), 727-742.

[John Aldrich, Cesc Rossello, and Dirk Schlimm contributed to this entry].

The term PRIMITIVE ROOT was introduced by Leonhard Euler (1707-1783), according to Dickson, vol. I, page 181.

In "Demonstrationes circa residua ex divisione potestatum per numeros primos resultantia," Novi commentarii academiae scientiarum Petropolitanae 18 (1773), Euler wrote: "Huiusmodi radices progressionis geometricae, quae series residuorum completas producunt, primitivas appellabo" [Heinz Lueneburg].

Primitive root is found in English in 1811 in An Elementary Investigation of the Theory of Numbers by Peter Barlow [James A. Landau].

The method of PRINCIPAL COMPONENTS was introduced by H. Hotelling in  "Analysis of a Complex of Statistical Variables into Principal Components," Jrnl. Educ. Psychol. &ldquo:IV, (1933). On p. 421: "We..determine the components, not exceeding n in number, and perhaps neglecting those whose contributions to the total variance are small. This we shall call the method of principal components." (OED)

The term PRINCIPAL GROUP was introduced by Felix Klein (1849-1925) (Katz, page 791).

PRINCIPAL SQUARE ROOT appears in 1898 in Text-Book of Algebra by G. E. Fisher and I. J. Schwatt, according to Manning (1970).

The term PRINCIPLE OF CONTINUITY was coined by Poncelet (Kline, page 843).

PRINCIPLE OF INDIFFERENCE/INSUFFICIENT REASON. In his Treatise on Probability (1921) J. M. Keynes re-named the principle of insufficient reason the principle of indifference for he thought the older term "clumsy and unsatisfactory. The essence of the principle was, "equal probabilites must be assigned to each of several alternatives, if there is an absence of positive ground for assigning unequal ones."

The term principle of insufficient reason was used by Johannes von Kries in his probability textbook in 1871, according to The Emergence of Probability by Ian Hacking [Hans Fischer].

The principle is usually traced to Jakob (Jacques) Bernoulli’s Ars Conjectandi (1713). Later the principle provided a justification for the use of a uniform prior in problems of inverse probability. In the course of the 19^th century its use in this role was subject to increasingly heavy criticism.  R. A. Fisher echoed these criticisms when he discussed the application of the principle to Bayes’s problem of inference to the probability of success in Bernoulli trials: "Apart from evolving a vitally important piece of knowledge, that of the exact form of the distribution of p, out of complete ignorance, it is not even a unique solution. For ... we might equally have measured probability upon an entirely different scale ..." "On the Mathematical Foundations of Theoretical Statistics" (Phil. Trans. Royal Soc. Ser. A. 222, (1922), p. 326).

See also BAYES, INVERSE PROBABILITY and UNIFORM DISTRIBUTION.

[This entry was contributed by John Aldrich, based on Hacking (op. cit.) and Hald (1998)]

The term PRINCIPLE OF THE PERMANENCE OF EQUIVALENT FORMS was introduced by George Peacock (1791-1858) (Eves, page 377).

PRISM is found in English in Sir Henry Billingsley’s 1570 translation of Euclid’s Elements (OED2). See the Elements, XI, def.13.

PRISMATOID (as a geometric figure) occurs in the title Das Prismatoid, by Th. Wittstein (Hannover, 1860) [Tom Foregger].

Prismatoid is found in English in 1881 in Metrical geometry. An elementary treatise on mensuration by George Bruce Halsted: "&ldquo:XIV. A prismatoid is a polyhedron whose bases are any two polygons in parallel planes, and whose lateral faces are determined by so joining the vertices of these bases that each line in order forms a triangle with the preceding line and one side of either base. REMARK. This definition is more general than &ldquo:XIII., and allows dihedral angles to be concave or convex, though neither base contain a reentrant angle. Thus, BB’s might have been joined instead of A’sC" [University of Michigan Digital Library].

PRISMOID is found in 1704 in Lexicon Technicum: "I, Prismoid, is a solid Figure, contained under several Planes whose Bases are rectangular Parallelograms, parallel and alike situate" [OED2].

The PRISONER’S DILEMMA was posed by A. W. Tucker in 1950, when addressing an audience of psychologists at Stanford University, where he was a visiting professor. The OED entry includes an account it received from Tucker, "The Prisoner’s Dilemma is my brain child. I concocted it at Stanford in early 1950 as a catchy example to enliven a semi-popular talk on Game Theory... My example became known by the ‘grapevine’, but I did not publish it." It is discussed in the 1957 book by Luce & Raiffa Games & Decisions.

PROBABILISTIC is found in Tosio Kitagawa, Sigeru Huruya, and Takesi Yazima, The probabilistic analysis of the time-series of rare event, Mem. Fac. Sci. Kyusyu Univ., Ser. A 2 (1942).

The English words PROBABILITY and CHANCE were given new meanings when the mathematics of Pascal, Fermat and Huygens was translated and developed. (The OED traces "probability" to the mid 16^th century and "chance" to the turn of the 14^th.)

The origins of probability theory are usually traced to the 1654 correspondence between Pascal and Fermat, Les Lettres de Blaise Pascal (pp.188-229), or in 20^th century English translation. Probability (or probabilité) does not figure in the letters and the only word a modern reader might want to translate as probability is le hasard, used by Fermat in his letter of September 25^th: "La somme des hasards... ce qui fait en tout 17/27." Probability in its modern sense is used the last chapter of La Logique, ou L’Art de Penser (1682) by Pascal’s friends Arnauld and Nicole. See La Logique de Port-Royal pp. 365ff.

The word kans (chance) was used repeatedly by Huygens in his Dutch work Van Rekeningh in Spelen van Geluck. (Kees Verduin) The Latin version of this work, De Ratiociniis in Ludo Aleae (1657)), was translated into English as The Value of All Chances ... (1714). Here chances are possibilities or opportunities: e.g. "If the number of Chances I have to gain a, be p, and the number of Chances I have to gain b, be q. Supposing the Chances be equal; my Expectation will then be worth ap+bq / p+q." (Prop. III) The expression "chances are equal," which is used a lot, means that the probabilities of the opportunities are the same. The word probability appears once in the expression "more probability" and once in "equal probability."

The term "probability" was much more important in De Moivre’s The Doctrine of Chances: or, a Method of Calculating the Probability of Events in Play (1718). De Moivre uses "probability" in its modern sense, e.g. "CASE I^st: To find the Probability of throwing an Ace in two throws of one Die." The book’s opening proposition connects chance and probability: "The Probability of an Event is greater or less, according to the number of Chances by which it may happen, compared with the whole number of Chances by which it may happen or fail." Chances are counted and probabilities are derived from them. In his Essay (1767) Bayes re-defined chance when he wrote, "By chance I mean the same as probability." (Definition 6)

Bayes’s title, An Essay towards solving a Problem in the Doctrine of Chances, illustrates the common practice in 18^th century England of referring to the subject as the "doctrine of chances." In the 19^th century probability was more likely to be in the title: e.g. Laplace’s Théorie Analytique des Probabilités, (1812) and, in English, Lubbock & Drinkwater-Bethune’s On Probability (1830) and De Morgan’s Essay on Probabilities (1838). The phrase theory of probability came into use in English after 1860, a fashion set by Todhunter’s A History of the Mathematical Theory of Probability (1865). Bertrand set the fashion for titles in French with his Calcul des Probabilités (1889).

Since 1840 or so there has been a continuing debate on the nature of probability. Everyone with an interest in probability--mathematicians, philosophers, physicists, economists, etc.--has contributed and a special vocabulary has evolved. The most common terms, such as subjective and objective, are used in a variety of senses and have a complex history. Poisson distinguished two concepts in his Recherches sur la Probabilité des Jugements en Matières Criminelles et Matiere Civile (1837): probabilité, a question of "the reason we have to believe that [an event] will or will not occur," and chance, a question of "events in themselves and independent of the knowledge we have of them." More recently Carnap Logical Foundations of Probability (1950) used "probability₁" for probability as degree of confirmation and "probability₂" for probability as relative frequency. Savage Foundations of Statistics (1954) called his probability construction "personal probability." (See I. Hacking The Emergence of Probability and L. Daston "How Probabilities came to be Objective and Subjective," Historia Mathematica, 21, (1994), 330-344. The Poisson translations are Daston’s.)

When Kolmogorov axiomatised probability in the Grundbegriffe der Wahrscheinlichkeitsrechnung (1933) he exploited the analogy between the measure of a set and the probability of an event. The development generated new probability terms. A JSTOR search produced the following appearances in English.

Probability measure appears in J. L. Doob "Stochastic Processes with an Integral Valued Parameter," Transactions of the American Mathematical Society, 44, (1938), 87-150: "any non-negative completely additive function of point sets, defined on a Borel field of sets of some abstract space Ω will be called a probability measure if the space Ω is itself in the field of definition and if the set function is defined as 1 on the space Ω."

Probability space appears in J. L. Doob & R. A. Leibler "On the Spectral Analysis of a Certain Transformation," American Journal of Mathematics, 65, (1943), 263-272: "we consider an abstract space Ω with a measure P of Lebesgue type--that is, completely additive and non-negative on some Borel field of Ω--with P(Ω) = 1; that is we consider a probability space." (p. 268)

Chance variable had a brief career around 1935-40 in the sense of random variable. See e.g. Doob’s paper on martingales, "Regularity Properties of Certain Families of Chance Variables," Transactions of the American Mathematical Society, 47, 455-486.

The word probabilist has been in English since the 17^th century (OED) but it has only been in common use in the sense of a specialist in probability theory since the 1950s (JSTOR). An early sighting is in a 1946 letter from R. A. Fisher "In Paris recently I found an interesting and perhaps useful distinction being made between statisticians and probabilists, broadly speaking putting me in the first class and Cramer in the second." Statistical Inference and Analysis: Selected Correspondence of R. A. Fisher (p. 331)

This entry was contributed by John Aldrich. A complete list of the probability and statistics terms on this web site is here. See also Symbols in Probability on the Symbols in Probability and Statistics page.

PROBABILITY DENSITY FUNCTION. Probability function appears in J. E. Hilgard, "On the verification of the probability function," Rep. Brit. Ass. (1872).

Wahrscheinlichkeitsdichte appears in 1912 in Wahrscheinlichkeitsrechnung by A. A. Markoff (David, 1998).

In J. V. Uspensky, Introduction to Mathematical Probability (1937), page 264 reads "The case of continuous F(t), having a continuous derivative f(t) (save for a finite set of points of discontinuity), corresponds to a continuous variable distributed with the density f(t), since F(t) = integral from -infinity to t f(x)dx" [James A. Landau].

Probability density appears in 1939 in H. Jeffreys, Theory of Probability: "We shall usually write this briefly P(dx|p) = f’s(x)dx, dx on the left meaning the proposition that x lies in a particular range dx. f’s(x) is called the probability density" (OED2).

Probability density function appears in 1946 in an English translation of Mathematical Methods of Statistics by Harald Cramér. The original appeared in Swedish in 1945 [James A. Landau].

See also the Probability and Statistics section of the companion page on the history of mathematical notation.

PROBABILITY DISTRIBUTION appears in a paper published by Sir Ronald Aylmer Fisher in 1920 (p. 758) [James A. Landau].

PROBABILITY DISTRIBUTIONS and STOCHASTIC PROCESSES, NAMES FOR. Several patterns in naming can be identified. The object can be named after a person associated with it (EPONYMY), e.g. CAUCHY, GAUSSIAN, MARKOV, POISSON, WEIBULL, WIENER, WISHART. The object can take its name from the phenomenon with which it is associated, e.g. BRANCHING PROCESS, BROWNIAN MOTION, ERROR, or from the mathematical construction on which it is based, e.g. BETA, BINOMIAL, EXPONENTIAL, GAMMA. The mathematical construction may itself be named after a person, as in the case DIRICHLET. In some cases the symbol used for the random variable has given its name to the distribution, e.g. CHI-SQUARED and F. Systems of distributions, e.g. the PEARSON CURVES, generate ‘family’ names for the distributions: so the beta distribution is also known as a Pearson Type I curve.

PROBABILITY GENERATING FUNCTION. A. de Moivre used this technique when he found the number of chances of throwing s points with n dice in his Miscellanea Analytica (1730); the analysis is reproduced in the 2^nd edition of the Doctrine of Chances (1738). Generating functions were used by other 18^th century authors, including Thomas Simpson in On the Advantage of Taking the Mean of a Number of Observations (1755). Laplace gave the technique its name and developed it further; Book I of his Théorie Analytique des Probabilités (1812) is called Calcul des Functions Génératrices.  See Hald (1990, pp. 210-2)

The term probability generating function has been current only since the 1940s. The earliest result from a JSTOR search was M. S. Bartlett "The Present Position of Mathematical Statistics," Journal of the Royal Statistical Society, 103, (1940), 1-29. Perhaps the growing use of other types of generating function, including the moment generating function and the cumulant generating function, made a more specific term desirable.

This entry was contributed by John Aldrich. See CHARACTERISTIC FUNCTION and MOMENT GENERATING FUNCTION.

PROBABILITY INTEGRAL TRANSFORMATION. The term first appears in E. S. Pearson “The Probability Integral Transformation for Testing Goodness of Fit and Combining Independent Tests of Significance,” Biometrika, 30, (1938), 134-148. Pearson (p. 135) states that the idea had been used in recent work by R. A. Fisher, Karl Pearson and Neyman. However Stephen M. Stigler indicates an earlier use, writing in “Simon Newcomb, Percy Daniell, and the History of Robust Estimation 1885-1920,” Journal of the American Statistical Association, 68, (1973), p. 876 that the transformation was used “apparently for the first time” by P. J. Daniell “Observations Weighted According to Order,” American Journal of Mathematics, 42, (1920), 222-236. [John Aldrich]

PROBABLE ERROR appears in a non-technical sense 1812 in Phil. Mag.: "All that can be gained is, that the errors are as trifling as possible--that they are equally distributed--and that none of them exceed the probable errors of the observation" (OED2).

According to Hald (p. 360), Friedrich Wilhelm Bessel (1784-1846) introduced the term probable error (wahrscheinliche Fehler) without detailed explanation in 1815 in "Ueber den Ort des Polarsterns" in Astronomische Jahrbuch für das Jahr 1818, and in 1816 defined the term in "Untersuchungen über die Bahn des Olbersschen Kometen" in Abh. Math. Kl. Kgl. Akad. Wiss., Berlin. Bessel used the term for the 50% interval around the least-squares estimate.

Probable error is found in 1852 in Report made to the Hon. Thomas Corwin, secretary of the treasury by Richard Sears McCulloh. This book uses the term four times, but on the one occasion where a computation can be seen the writer takes two measurements and refers to the difference between them as the "probable error" [University of Michigan Digital Library].

Probable error is found in 1853 in A dictionary of science, literature & art edited by William Thomas Brande: "... the probable error is the quantity, which is such that there is the same probability of the difference between the determination and the true absolute value of the thing to be determined exceeding or falling short of it. Thus, if twenty measurements of an angle have been made with the theodolite, and the arithmetical mean or average of the whole gives 50° 27’s 13"; and if it be an equal wager that the error of this result (either in excess or defect) is less than two seconds, or greater than two seconds, then the probable error of the determination is two seconds" [University of Michigan Digital Library].

Probable error is found in 1853 in A collection of tables and formulae useful in surveying, geodesy, and practical astronomy by Thomas Jefferson Lee. The term is defined, in modern terminology, as the sample standard deviation times .674489 divided by the square root of the number of observations [James A. Landau; University of Michigan Digital Library].

Probable error is found in 1855 in A treatise on land surveying by William Mitchell Gillespie: "When a number of separate observations of an angle have been made, the mean or average of them all, (obtained by dividing the sum of the readings by their number,) is taken as the true reading. The ’sProbable error’s of this mean, is the quantity, (minutes or seconds) which is such that there is an even chance of the real error being more or less than it. Thus, if ten measurements of an angle gave a mean of 350 18’s, and it was an equal wager that the error of this result, too much or too little, was half a minute, then half a minute would be the ’sProbable error’s of this determination. This probable error is equal to the square root of the sum of the squares of the errors (i. e. the differences of each observation from the mean) divided by the number of observations, and multiplied by the decimal 0.674489. The same result would be obtained by using what is called ’sThe weight’s of the observation. It is equal to the square of the number of observations divided by twice the sum of the squares of the errors. The ’sProbable error’s is equal to 0.476936 divided by the square root of the weight" [University of Michigan Digital Library].

Probable error is found in 1865 in Spherical astronomy by Franz Brünnow (an English translation by the author of the second German edition): "In any series of errors written in the order of their absolute magnitude and each written as often as it actually occurs, we call that error which stands exactly in the middle, the probable error" [University of Michigan Digital Library].

In 1872 Elem. Nat. Philos. by Thomson & Tait has: "The probable error of the sum or difference of two quantities, affected by independent errors, is the square root of the sum of the squares of their separate probable errors" (OED2).

In 1889 in Natural Inheritance pp. 57-8 Galton criticized the term probable error, saying the term was "absurd" and "quite misleading" because it does not refer to what it seems to, the most probable error, which would be zero. He suggested the term Probability Deviation be substituted, opening the way for Pearson to introduce the term standard deviation (Tankard, p. 48).

"Probable error" went out of use in the early 20th century to be replaced by "standard error": the probable error is 0.67449 times the standard error. R. A. Fisher, one of those who adopted the standard error, remarked in Statistical Methods for Research Workers (1925, p. 48) "The common use of the probable error is its only recommendation." [John Aldrich]

See also STANDARD ERROR.

The term PROBABLE PRIME TO BASE a was suggested by John Brillhart [Carl Pomerance et al., Mathematics of Computation, vol. 35, number 151, July 1980, page 1021].

PROBIT. The OED and David (2001) refer to C. I. Bliss "The Method of Probits," Science, 79, (1934), 38-9: "These arbitrary probability units have been termed ‘probits’" (p. 39). Whether Bliss was responsible for the term himself is unclear. D. J. Finney Probit Analysis 2^nd edition (1952, pp. 42-6) traces the underlying principle back to Fechner and his work on psychophysics in 1860 but the probit terminology seems to have arrived with Bliss. R. A. Fisher collaborated with Bliss (see his The Case of Zero Survivors in Probit Assays Annals of Applied Biology, 22: 164-165 (1935)) and he wrote about probit analysis in his book The Design of Experiments (1935). The publicity brought the subject to the attention of statisticians generally.

PROBLEM OF THE NILE. At the end of his paper Uncertain Inference Proceedings of the American Academy of Arts and Science, 71: 245-258 (1936) R. A. Fisher posed the following problem:

The agricultural land of a pre-dynastic Egyptian village is of unequal fertility. Give the height to which the Nile will rise, the fertility of every portion of it is known with exactitude, but the height of the flood affects different parts of the territory unequally. It is required to divide the area, between the several households of the village, so that the yields of the lots assigned to each shall be in pre-determined proportion, whatever may be the height to which the river rises.

Fisher added, "If this problem is capable of a general solution, then ... one of the primary problems of uncertain inference will have reached its complete solution."  Later writers usually referred to this as Fisher’s Problem of the Nile, as in the title of a 1946 paper by D. G. Kendall in the journal Nature.

PRODUCT (in multiplication). According to the OED2, Albertus Magnus (1193-1280) used productum in his Metaphysicorum.

Fibonacci (1202) used factus ex multiplicatione and also the phrase "contemptum sub duobus numeris" (Smith, vol. 1).

Art of Nombryng (about 1430) uses both product and sum for the result in multiplication: "In multiplicacioun 2 nombres pryncipally ben necessary,..the nombre multiplying and the nombre to be multipliede... Also..the 3 nombre, the whiche is clepide product or pervenient. [...] Multiplie .3. by hym-selfe, and þe some of alle wolle be 9" (OED2).

Sum was used for the result in multiplication by Pacioli (1494), Ortega (1512; 1515), and Recorde (c. 1542; 1558) (Smith, vol. 1).

In 1542 Robert Recorde in Ground of Artes (1575) used the obsolete term offcome: "The ofcome or product" (OED2). Offcome also appears in English in 1570 in Billingsley’s translation of Euclid.

According to Smith (vol. 1), Licht (1500) used simply productus, dropping the numerus from numerus productus. Clichtoveus (1503) used both numerus productus and tota summa. Fine (1530) used sum as well as numerus productus. Glareanus (1538) used summa producta. Ramus (1569) used factus.

PROGRAM (of research) often appears in writing about mathematics, e.g. as when Cajori (vol. II, (1929), p. 283) wrote, "The contribution of Leibniz to symbolic logic was a program, rather than an actual accomplishment. He set up an ideal for others to approach." But the word is also used in such permanent constructions as ERLANGEN PROGRAM and HILBERT’S PROGRAM.

PROGRAM and PROGRAMMING (computing.) The OED gives two meanings for the noun program: (1) "A sequence of operations that a machine can be set to perform automatically" with earliest reference from 1945: J. P. Eckert et al. Description of ENIAC (PB 86242) (Moore School of Electr. Engin., Univ. of Pennsylvania) 1 "The intended use of the ENIAC is to compute large families of solutions all based on the same program of operations." (2) "A series of coded instructions which when fed into a computer will automatically direct its operation in carrying out a specific task" with earliest reference from 1946: Nature 20 Apr. 527/2 "Control of the programme of the operation of the machine [sc. ENIAC] is also through electrical circuits."

The verb to program appears in J. P. Eckert et al. Description of ENIAC (PB 86242) (Moore School of Electr. Engin., Univ. of Pennsylvania) B-4 "In this fashion, problems involving numbers of multiplications far in excess of 24 can be programmed."

PROGRAM and PROGRAMMING (optimization.) Programming appears in the title, "The Programming of Interdependent Activities: General discussion" by Marshall K. Wood and George B. Dantzig (obituary) in Econometrica, 17, July-October, 1949. Program appears in Part II of the paper by Dantzig alone, "Programming of Interdependent Activities: II Mathematical Model," Econometrica, 17, p. 203: "A set of values [satisfying the constraints] is called a feasible program." [James A. Landau].

Linear programming. Programming in a Linear Structure is the title of a work by George B. Dantzig published in 1948. Linear programming was used in 1949 by Dantzig’s in "Programming of Interdependent Activities: II Mathematical Model," Econometrica, 17, p. 203: "It is our purpose now to discuss the kinds of restrictions that fit naturally into linear programming" (OED2).

According to Linear Programming and Network Flows by Mokhtar S. Bazaraa, John J. Jarvis, and Hanif D. Sherali, 2nd Edition, 1990), the term linear programming was coined by the economist and mathematician Tjalling Charles Koopmans (1910-1985) in the summer of 1948 while he and George B. Dantzig strolled near the beach in Santa Monica, California.

In an interview of Merrill Flood conducted by Albert Tucker on May 14, 1984, Flood indicated that he and John Tukey coined the term linear programming:

Flood: One of the friendly arguments that Tjallings Koopmans and I had concerned an appropriate name for what is now known as linear programming theory. When I was responsible for organizing the December meeting of the Allied Social Science Associations in Cleveland, probably 1947, I wanted to include a session of what was then commonly referred to as input-output analysis, after the work of Wassily Leontief. Tjallings agreed to organize such a session for the meeting, and we met in California to discuss the arrangements just prior to Neyman’s Second Berkeley Symposium. Actually we discussed this while enroute from Stanford to Berkeley in a car whose other passengers were John Tukey, Francis Dresch, and a Stanford mathematician (Spencer?) who was driving. I knew a bit about Leontief’s work because of the work under Marshall Wood, by George Dantzig and others, that had been pushed and encouraged by Duane Evans, who was then at the Bureau of Labor Statistics - because of my position as Chief Civilian Scientist on the War Department General Staff, with some minor responsibility for the effort in the Air Force under Marshall Wood. When Tjallings and I were trying to decide what to call the session in Cleveland I was unhappy with the input-output analysis title and wanted something that was broader and peppier, partly because of the related Air Force work. Tjallings proposed "activity analysis" as a name for the session, with some support from the economist Dresch, but Tukey and I were not satisfied. As you know, John Tukey is very good at creating good names for things, and between us John and I soon settled upon "linear programming" as an excellent name for the session. As I recall vaguely now Tjallings did not call the Cleveland session "linear programming" but his own 1948 Chicago conference went by that name even though he used ’sactivity analysis’s in the title of his published proceedings. I forget just how Tukey and I arrived at the name ’slinear programming’s, but it has certainly stuck. I doubt that Tukey even remembers the California incident now.

Tucker: The first paper by George Dantzig and Marshall Wood was called "Programming in a Linear Structure".

Flood: Well, it is possible that is where we got the idea.

Tucker: And the two words, interchanged, were pulled out of that. I think that’s the official story.

Flood: When was that paper? Was that before that, do you think? It may be the other way around.

Tucker: Well, that paper appears in the Activity Analysis volume. But it appeared earlier. The Activity Analysis volume was published in 1951. 1 think that the paper had appeared about two years before that.

Flood: That would be later. I suspect that it came the other way around. I’sm remembering vaguely the conversation Tukey and I had, and I don’st remember any awareness of any such terminology by Dantzig and company.

Nonlinear programming appears in the title "Nonlinear Programming" by H. W. Kuhn and A. W. Tucker in Jerzy Neyman (ed.), Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability (1950) [James A. Landau].

Mathematical programming occurs in the title "Mathematical Programming," by A. Henderson and R. Schlaifer, Harvard Business Review 32, May-June 1954 [James A. Landau].

Dynamic programming is found in Richard Bellman, Dynamic Programming of Continuous Processes, The RAND Corporation, Report R-271, July 1954 [James A. Landau].

Quadratic programming is found in 1958 the title On Quadratic Programming by E. W. Barankin and R. Dorfman [James A. Landau].

PROGRESSION. Boethius (c. 510), like the other Latin writers, used the word progressio (Smith vol. 2, page 496).

PROJECTION. The use of the term in functional analysis and matrix theory can be traced to M. H. Stone’s Linear Transformations in Hilbert Space 1932. Stone used the word in two ways, first (p. 23) for the image and then (pp. 70-1) for the transformation producing the image. After proving a theorem about the action of such transformations he wrote, “In the terminology of Hilbert and his followers such a transformation or operator and its associated matrix ... are called "Einzeltransformation" or "Einzeloperator" or "Einzelmatrix": this terminology does not seem to admit a graceful or apt translation into English so that we shall use the term "projection", being justified by the theorem.”

See the entry HILBERT SPACE.

PROJECTIVE GEOMETRY. In his account of the origins of projective geometry Katz (1993) mentions Pascal, Desargues and Monge before saying that J.-V.Poncelet composed the first text in synthetic projective geometry: his Traité des Propriétés Projectives of 1822. See here for an extract from Poncelet’s Introduction.

The OED finds the term projective geometry used in English in 1885 in Charles Leudesdorf’s Elements of Projective Geometry, a translation of Cremona’s Elementi di geometria proiettiva of 1873.

PROPER FRACTION appears in English in 1674 in Samuel Jeake Arithmetic (1701): "Proper Fractions always have the Numerator less than the Denominator, for then the parts signified are less than a Unit or Integer" (OED2).

PROPER VALUE and VECTOR. See Eigenvalue.

PROPORTION. See ratio and proportion.

PROPORTIONAL HAZARD MODEL. The model and the name were introduced by D. R. Cox in "Regression Models and Life Tables (with discussion)," Journal of the Royal Statistical Society, B 34 (1972), 187-220.

PROPOSITIONAL FUNCTION appears in 1905 without explanation in a footnote in Bertrand Russell "On Denoting," Mind, 14, (1905), p. 480. Russell is more expansive in "The Theory of Implication," American Journal of Mathematics, 28, (1906), p. 163: "Such expressions are functions whose values are propositions; hence we call them propositional functions."

PROPOSITIONAL CALCULUS occurs in 1903 in the The Principles of Mathematics by Bertrand Russell, p. 12: "It is not with such entities that we are concerned in the propositional calculus, but with genuine propositions."  (OED2).

PROTRACTOR appears in 1658 in Edward Phillips’s New World of English Words: "Protractor, a certain Mathematical instrument made of brasse, consisting of the Scale and Semicircle, used in the surveying of Land" [OED2].

PSEUDO-PARALLEL was apparently coined by Eduard Study (1862-1930) in 1906 Ueber Nicht-Euklidische und Linien Geometrie.

The term PSEUDOPRIME appears in Paul Erdös, "On pseudoprimes and Carmichael numbers," Publ. Math., 4, 201-206 (1956).

The term was also used by Ivan Niven (1915-1999) in "The Concept of Number," in Insights into Modern Mathematics, 23rd Yearbook, NCTM, Washington (1957), according to Kramer (p. 500). She seems to imply Niven coined the term.

PSEUDOSPHERE was coined by Eugenio Beltrami (1835-1900). He referred to a surface of negative curvature as pseudo-spherical.

PSYCHOMATHEMATICS. Henry Blumberg coined this term and used it in the article "On the technique of generalization" (AMM, 1940, pp. 451-462). He wrote: "By Psychomathematics, I understand, namely, that union of mathematics and psychology - using the latter in a broad, non technicals sense - whose function it is to explain how mathematical ideas arise, and to formulate heuristically helpful principles in mathematical exploration" [Carlos César de Araújo].

PSYCHOMETRICS is defined in the OED as "The science of measuring mental capacities and processes; the application of methods of measurement to the various branches of psychology." The OED’s earliest quotation is from 1930: Proc. & Addr. Amer. Assoc. Stud. Feeble-Minded &ldquo:XV. 94: "To most persons who know the term at all, psychometrics is fairly synonymous with the use of intelligence tests." The subject also embraced the field of psychophysics, so named by Gustav Theodor Fechner (1801-87) in 1859 as Psychophysik. The OED gives a quotation from Francis Galton: "Most of you are aware of the recent progress of what has been termed Psycho-physics, or the science of subjecting mental processes to physical measurements and to physical laws." Rep. Brit. Assoc. Adv. Sci. 1877 II. 95

PURE IMAGINARY is found in 1857 in "A Memoir Upon Caustics" by Arthur Cayley in the Philosophical Transactions of the Royal Society of London: "... the radius may be either a real or a pure imaginary distance ..." [University of Michigan Historical Math Collection].

PURE and APPLIED MATHEMATICS. In Book II of The Advancement of Learning (1605) Francis Bacon distinguished pure and mixed mathematics in much the way modern writers distinguish pure and applied mathematics:

The Mathematics are either pure or mixed. To the Pure Mathematics are those sciences belonging which handle quantity determinate, merely severed from any axioms of natural philosophy; and these are two, Geometry and Arithmetic; the one handling quantity continued, and the other dissevered. Mixed hath for subject some axioms or parts of natural philosophy, and considereth quantity determined, as it is auxiliary and incident unto them. For many parts of nature can neither be invented with sufficient subtilty, nor demonstrated with sufficient perspicuity, nor accommodated unto use with sufficient dexterity, without the aid and intervening of the mathematics; of which sort are perspective, music, astronomy, cosmography, architecture, enginery, and divers others.

In the Mathematics I can report no deficience, except it be that men do not sufficiently understand the excellent use of the Pure Mathematics, in that they do remedy and cure many defects in the wit and faculties intellectual. ... And as for the Mixed Mathematics, I may only make this prediction, that there cannot fail to be more kinds of them, as nature grows further disclosed.

The first edition of the Encyclopaedia Britannica (1768-1771) has: "Pure mathematics have one peculiar advantage, that they occasion no disputes among wrangling disputants, as in other branches of knowledge; and the reason is, because the definitions of the terms are premised, and every body that reads a proposition has the same idea of every part of it."

In the course of the 19^th century the term mixed mathematics was replaced by applied mathematics. The Quarterly Journal of Pure and Applied Mathematics started publication in 1857 and its title echoed that of Liouville’s journal, Journal des mathématiques pures et appliquées, ou Recueil mensuel de mémoires sur les diverses parties des mathématiques (Tome 1) founded in 1836. In the 19^th and 20^th centuries applied mathematics was usually mathematics applied to physics or even just to mechanics, so its scope was not quite the same as Bacon’s "music, astronomy, cosmography, architecture, enginery, and divers others."  

[This entry was contributed by John Aldrich.]

PYRAMID. According to Smith (vol. 2, page 292), "the Greeks probably obtained the word ’spyramid’s from the Egyptian. It appears, for example, in the Ahmes Papyrus (c. 1550 B. C.). Because of the pyramidal form of a flame the word was thought by medieval and Renaissance writers to come from the Greek word for fire, and so a pyramid was occasionally called a ’sfire-shaped body.’s"

The PYTHAGOREAN THEOREM (named after Pythagoras (ca. 569 BC-ca. 475 BC) is the 47th Proposition of the first book of Euclid’s Elements. Euclid did not mention Pythagoras but, according to Heath’s edition of the Elements, later writers, including Apollodorus, Cicero, Proclus, Plutarch and Athenaeus, referred to the proposition as a discovery of Pythagoras.

The term Pythagorean theorem appears in English in 1726 in A New Mathematical Dictionary, 2nd ed., by Edmund Stone.

Pythagorean axiom appears in 1912 in G. Kapp, Electr.: "The well-known Pythagorean axiom that the sum of the squares of the kathetes in a rectangular triangle is equal to the square of the hypotenuse" (OED2).

Some early twentieth-century U. S. dictionaries have Pythagorean proposition, rather than Pythagorean theorem.

[Randy K. Schwartz, John G. Fauvel, Leo Rogers, and John Aldrich contributed to this entry.]

PYTHAGOREAN TRIPLE. Pythagorean triad appears in 1909 in Webster’s New International Dictionary.

Pythagorean number triplet appears in 1916 in Historical Introduction to Mathematical Literature by George Abram Miller: "Pythagorean number triplets appear also in some of the Hindu writings which antedate the lifetime of Pythagoras."

Pythagorean triple is found in March 1937 in The Mathematics Teacher: "Later in the book the quest for primitive Pythagorean triples, a beautiful illustration, by the way, of the methods of mathematical reasoning, leads just as naturally to a consideration of ’sFermat’s last theorem’s and other topics in the theory of numbers." The term may be much older, however.