Earliest Uses of Symbols for Variables
Last revision: June 23, 2017
Greek letters. The use of letters to represent general numbers
goes back to Greek antiquity. Aristotle frequently used single
capital letters or two letters for the designation of magnitude or
number (Cajori vol. 2, page 1).
Diophantus (fl. about 250-275) used a Greek letter with an accent to
represent an unknown. G. H. F. Nesselmann takes this symbol to be
the final sigma and remarks that probably its selection was prompted
by the fact that it was the only letter in the Greek alphabet which
was not used in writing numbers. However, differing opinions exist
(Cajori vol. 1, page 71).
In 1463, Benedetto of Florence used the Greek letter rho for an
unknown in Trattato di praticha d'arismetrica. (Franci and
Rigatelli, p. 314)
Roman letters. In Leonardo of Pisa's Liber abbaci
(1202) the representation of given numbers by small letters is found
(Cajori vol. 2, page 2).
Jordanus Nemorarius (1225-1260) used letters to replace numbers.
Christoff Rudolff used the letters a, c, and d to
represent numbers, although not in algebraic equations, in Behend
vnnd Hubsch Rechnung (1525) (Cajori vol. 1, page 136).
Michael Stifel used q (abbreviation for quantita (which
Cardan had already done) but he also used A, B, C, D, and
F, for unknowns in 1544 in Arithmetica integra (Cajori
vol. 1, page 140).
Girolamo Cardan (1501-1576) used the letters a and b to
designate known numbers in De regula aliza (1570) (Cajori vol.
1, page 120).
In 1575 Guilielmus Xylander translated the Arithmetica of
Diophantus from Greek into Latin and used N (numerus)
for unknowns in equations (Cajori vol. 1, page 380).
In 1591 Francois Vieta (1540-1603) was the first person to use letters
for unknowns and constants in algebraic equations. He used vowels for
unknowns and consonants for given numbers (all capital letters) in
In artem analyticem isogoge. Vieta wrote:
Quod oopus, ut arte aliqua juventur, symbolo constanti et
perpetuo ac bene conspicuo date magnitudines ab incertis quaesititiis
distinguantur ut [illegible in Cajori] magnitudines quaesititias
elemento A aliave litera volcali, E, I, O, V, Y [illegible in
Cajori] elementis B, G, D, aliisve consonis designando. [As one
needs, in order that one may be aided by a particular device, some
unvarying, fixed and clear symbol, the given magnitudes shall be
distinguished from the unknown magnitudes with the letter A or
with another vowel E, I, O, U, Y, the given ones with the
letters B, G, D or other consonants.]
(Cajori vol. 1, page 183, and vol. 2, page 5).
Thomas Harriot (1560-1621) in Artis Analyticae Praxis, ad
Aequationes Algebraicas used lower case vowels for unknowns and
lower case consonants for known quantities.
Descartes' use of z, y, x. The following is from
Cajori (vol 1, page 381):
The use of z, y, x . . . to represent unknowns is due to
René Descartes, in his La géometrie (1637).
Without comment, he introduces the use of the first letters of the
alphabet to signify known quantities and the use of the last
letters to signify unknown quantities. His own langauge is:
"...l'autre, LN, est (1/2)a la moitié de l'autre
quantité connue, qui estoit multipliée par z,
que ie suppose estre la ligne inconnue." Again: "...ie considere
... Que le segment de la ligne AB, qui est entre les poins
A et B, soit nommé x, et quie BC
soit nommé y; ... la proportion qui est entre les
costés AB et BR est aussy donnée, et ie
la pose comme de z a b; de façon qu' AB
estant x, RB sera bx/z, et la toute
CR sera y = bx/z. ..." Later he says: "et
pour ce que CB et BA sont deux quantités
indeterminées et inconnuës, ie les nomme, l'une y;
et l'autre x. Mais, affin de trouver le rapport de l'une a
l'autre, ie considere aussy les quantités connuës qui
determinent la description de cete ligne courbe: comme GA que
je nomme a, KL que je nomme b, et NL,
parallele a GA, que ie nomme C." As co-ordinates he
uses later only x and y. In equations, in the third
book of the Géométrie, x predominates. In
manuscripts written in the interval 1629-40, the unknown z
occurs only once. In the other places x and y occur.
In a paper on Cartesian ovals, prepared before 1629, x alone
occurs as unknown, y being used as a parameter. This is the
earliest place in which Descartes used one of the last letters of the
alphabet to represent an unknown. A little later he used x, y,
z again as known quantities.
Some historical writers have focused their attention upon the
x, disregarding the y and z, and the other
changes in notation made by Descartes; these wrtiers have endeavored
to connect this x with older symbols or with Arabic words.
Thus, J. Tropfke, P. Treutlein, and M. Curtze advanced the view that
the symbol for the unknown used by early German writers, 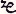 looked so much like an x
that it could easily have been taken as such, and that Descartes
actually did interpret and use it as an x. But Descartes'
mode of introducing the knowns a, b, c, etc., and the unknowns
z, y, x makes this hypothesis improbable. Moreover, G.
Eneström has shown that in a letter of March 26, 1619, addressed
to Isaac Beeckman, Descartes used the symbol
looked so much like an x
that it could easily have been taken as such, and that Descartes
actually did interpret and use it as an x. But Descartes'
mode of introducing the knowns a, b, c, etc., and the unknowns
z, y, x makes this hypothesis improbable. Moreover, G.
Eneström has shown that in a letter of March 26, 1619, addressed
to Isaac Beeckman, Descartes used the symbol 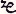 as a symbol in form distinct from x, hence
later could not have mistaken it for an
as a symbol in form distinct from x, hence
later could not have mistaken it for an 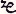 . At one time, before 1637, Descartes used x
along the side of
. At one time, before 1637, Descartes used x
along the side of 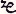 ; at that
time x, y, z are still used by him as symbols for known
quantities. German symbols including the
; at that
time x, y, z are still used by him as symbols for known
quantities. German symbols including the 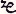 for x, as they are found in the algebra of
Clavius, occur regularly in a manuscript due to Descartes, the
Opuscules de 1619-1621.
for x, as they are found in the algebra of
Clavius, occur regularly in a manuscript due to Descartes, the
Opuscules de 1619-1621.
All these facts caused Tropfke in 1921 to abandon his old view on the
origin of x, but he now argues with force that the resemblance
of x and 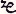 , and
Descartes' familiarity with
, and
Descartes' familiarity with 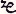 ,
may account for the fact that in the latter part of Descartes'
Géométrie the x occurs more frequently
than z and y. Eneström, on the other hand,
inclines to the view that the predominance of x over y
and z is due to typographical reasons, type for x being
more plentiful because of the more frequent occurrence of the letter
x, to y and z, in the French and Latin
languages.
,
may account for the fact that in the latter part of Descartes'
Géométrie the x occurs more frequently
than z and y. Eneström, on the other hand,
inclines to the view that the predominance of x over y
and z is due to typographical reasons, type for x being
more plentiful because of the more frequent occurrence of the letter
x, to y and z, in the French and Latin
languages.
Descartes introduced the equation ax + by = c,
which is still used to describe the equation of a line (Johnson, page
145).
Johnson says (on page 145):
The predominant use of the letter x to represent
an unknown value came about in an interesting way. During the
printing of La Geometrie and its appendix, Discours de La
Methode, which introduced coordinate geometry, the printer reached
a dilemma. While the text was being typeset, the printer began to run
short of the last letters of the alphabet. He asked Descartes if it
mattered whether x, y, or z was used in each of the
book's many equations. Descartes replied that it made no difference
which of the three letters was used to designate an unknown quantity.
The printer selected x for most of the unknowns, since the
letters y and z are used in the French language more
frequently than is x.
There are, however, other explanations for Descartes' use of x,
y, and z for unknowns. For example, the in the definition
of x in Webster's New International Dictionary
(1909-1916) and the subsequent second edition of the same dictionary,
it is claimed that "X was used as an abbreviation for Arabic
shei a thing, something, which, in the Middle Ages, was used to
designate the unknown, and was then prevailingly transcribed as
xei." Cajori says there is no evidence for this.
According to the Oxford English Dictionary (2nd ed.):
The introduction of x, y, z as symbols of unknown
quantities is due to Descartes (Géométrie,
1637), who, in order to provide symbols of unknowns corresponding to
the symbols a, b, c of knowns, took the last letter of the
alphabet, z, for the first unknown and proceeded backwards to
y and x for the second and third respectively. There is
no evidence in support of the hypothesis that x is derived
ultimately from the mediaeval transliteration xei of shei
"thing", used by the Arabs to denote the unknown quantity, or
from the compendium for L. res "thing" or radix "root"
(resembling a loosely-written x), used by mediaeval
mathematicians.
Descartes used letters to represent only positive numbers; a negative
number could be represented as -b (Cajori vol. 2, page 5).
John Hudde (1633-1704) was first to allow a letter to represent a
positive or negative number, in 1657 in De reductione
aequationum, published at the end of the first volume of F. Van
Schooten's second Latin edition of René Descartes'
Géométrie (Cajori vol. 2, page 5).
Jonas Moore wrote in Arithmetic (1660): "Note alwayes the
given quantities or numbers with Consonants, and those which are
sought with Vowels, or else the given quantities with the former
letters in the Alphabet, and the sought with the last sort of
letters, as z y x, &c. lest you make a confusion in your
work."
Complex numbers. The a + bi notation was
introduced by Leonhard Euler (1707-1783).
This page has been translated into Czech here.
Front Page |
Operation |
Grouping |
Relation |
Fractions and Decimals |
Constants |
Variables |
Functions |
Geometry |
Trigonometry |
Calculus |
Matrices and Vectors |
Set Theory and Logic |
Number theory |
Statistics |
Sources
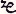 looked so much like an x
that it could easily have been taken as such, and that Descartes
actually did interpret and use it as an x. But Descartes'
mode of introducing the knowns a, b, c, etc., and the unknowns
z, y, x makes this hypothesis improbable. Moreover, G.
Eneström has shown that in a letter of March 26, 1619, addressed
to Isaac Beeckman, Descartes used the symbol
looked so much like an x
that it could easily have been taken as such, and that Descartes
actually did interpret and use it as an x. But Descartes'
mode of introducing the knowns a, b, c, etc., and the unknowns
z, y, x makes this hypothesis improbable. Moreover, G.
Eneström has shown that in a letter of March 26, 1619, addressed
to Isaac Beeckman, Descartes used the symbol 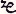 as a symbol in form distinct from x, hence
later could not have mistaken it for an
as a symbol in form distinct from x, hence
later could not have mistaken it for an 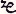 . At one time, before 1637, Descartes used x
along the side of
. At one time, before 1637, Descartes used x
along the side of 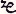 ; at that
time x, y, z are still used by him as symbols for known
quantities. German symbols including the
; at that
time x, y, z are still used by him as symbols for known
quantities. German symbols including the 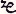 for x, as they are found in the algebra of
Clavius, occur regularly in a manuscript due to Descartes, the
Opuscules de 1619-1621.
for x, as they are found in the algebra of
Clavius, occur regularly in a manuscript due to Descartes, the
Opuscules de 1619-1621.
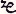 , and
Descartes' familiarity with
, and
Descartes' familiarity with 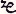 ,
may account for the fact that in the latter part of Descartes'
Géométrie the x occurs more frequently
than z and y. Eneström, on the other hand,
inclines to the view that the predominance of x over y
and z is due to typographical reasons, type for x being
more plentiful because of the more frequent occurrence of the letter
x, to y and z, in the French and Latin
languages.
,
may account for the fact that in the latter part of Descartes'
Géométrie the x occurs more frequently
than z and y. Eneström, on the other hand,
inclines to the view that the predominance of x over y
and z is due to typographical reasons, type for x being
more plentiful because of the more frequent occurrence of the letter
x, to y and z, in the French and Latin
languages.