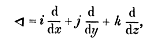Earliest Uses of Symbols of Calculus
Last revision: June 23, 2017
See here for a list
of calculus and analysis entrries on the Words pages.
Derivative. The symbols dx, dy, and dx/dy were introduced by
Gottfried Wilhelm Leibniz
(1646-1716) in a manuscript of November 11, 1675 (Cajori vol. 2, page 204).
f'(x) for the first derivative, f''(x) for the second derivative, etc., were introduced by
Joseph Louis Lagrange (1736-1813). In 1797 in
Théorie des fonctions analytiques
the symbols f'x and f''x are found; in the
Oeuvres, Vol. X,
"which purports to be a reprint of the 1806 edition, on p. 15, 17, one finds the corresponding parts
given as f(x), f'(x), f''(x), f'''(x)" (Cajori vol. 2, page 207).
In 1770 Joseph Louis Lagrange (1736-1813) wrote 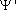 for
for 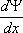 in his memoir
Nouvelle méthode pour résoudre les équations littérales par le moyen des séries
(Oeuvres, Vol. III, pp. 5-76).
The notation also occurs in a memoir by François Daviet de Foncenex in 1759
believed actually to have been written by Lagrange (Cajori 1919, page 256).
in his memoir
Nouvelle méthode pour résoudre les équations littérales par le moyen des séries
(Oeuvres, Vol. III, pp. 5-76).
The notation also occurs in a memoir by François Daviet de Foncenex in 1759
believed actually to have been written by Lagrange (Cajori 1919, page 256).
In 1772 Lagrange wrote u' = du/dx and
du = u'dx in "Sur une nouvelle espèce de calcul relatif à
la différentiation et à l'integration des quantités variables,"
Nouveaux Memoires de l'Academie royale des Sciences et Belles-Lettres de Berlin
(Oeuvres, Vol. III, pp. 451-478).
Dx y was introduced by
Louis François Antoine Arbogast
(1759-1803) in "De Calcul des dérivations et ses usages dans la théorie des suites
et dans le calcul différentiel," Strasbourg, xxii, pp. 404, Impr. de Levrault,
fréres, an VIII (1800). (This information comes from Julio González Cabillón;
Cajori indicates in his History of Mathematics that Arbogast introduced
this symbol, but it seems he does not show this symbol in A History of Mathematical
Notations.)
D was used by Arbogast in the same work, although this symbol
had previously been used by Johann Bernoulli (Cajori vol. 2, page
209). Bernoulli used the symbol in a non-operational sense (Maor,
page 97).
Partial derivative. The "curly d" was used in 1770 by
Antoine-Nicolas Caritat, Marquis de Condorcet
(1743-1794) in "Memoire sur les Equations aux différence partielles,"
which was published in
Histoire de L'Academie Royale des Sciences,
pp. 151-178, Annee M. DCCLXXIII (1773).
On page 152, Condorcet says:
Dans toute la suite de ce Memoire, dz & 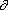 z désigneront ou deux
differences partielles de z,, dont une par rapport a x,
l'autre par rapport a y, ou bien dz sera une
différentielle totale, &
z désigneront ou deux
differences partielles de z,, dont une par rapport a x,
l'autre par rapport a y, ou bien dz sera une
différentielle totale, & 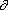 z une difference partielle.
[Throughout this paper, both dz &
z une difference partielle.
[Throughout this paper, both dz & 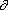 z will either denote two
partial differences of z, where one of them is with respect to
x, and the other, with respect to y, or dz and
z will either denote two
partial differences of z, where one of them is with respect to
x, and the other, with respect to y, or dz and
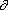 z will
be employed as symbols of total differential, and of partial
difference, respectively.]
z will
be employed as symbols of total differential, and of partial
difference, respectively.]
However, the "curly d" was first used in the form
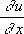 by
Adrien Marie Legendre
in 1786 in his "Memoire sur la manière de distinguer les maxima des minima dans le Calcul des Variations,"
Histoire de l'Academie Royale des Sciences,
Annee M. DCCLXXXVI (1786), pp. 7-37, Paris, M. DCCXXXVIII (1788).
On page 8, it reads:
by
Adrien Marie Legendre
in 1786 in his "Memoire sur la manière de distinguer les maxima des minima dans le Calcul des Variations,"
Histoire de l'Academie Royale des Sciences,
Annee M. DCCLXXXVI (1786), pp. 7-37, Paris, M. DCCXXXVIII (1788).
On page 8, it reads:
Pour éviter toute ambiguité, je
répresentarie par 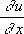 le coefficient de x dans la
différence de u, & par
le coefficient de x dans la
différence de u, & par 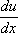 la différence complète de
u divisée par dx.
la différence complète de
u divisée par dx.
Legendre abandoned the symbol and it was re-introduced by
Carl Gustav Jacob Jacobi
in 1841. Jacobi used it extensively in his remarkable paper "De determinantibus Functionalibus"
Crelle’s Journal, Band 22, pp. 319-352, 1841
(
pp. 393-438 of vol. 1 of the Collected Works).
Sed quia uncorum accumulatio et legenti et scribenti
molestior fieri solet, praetuli characteristica d
differentialia vulgaria, differentialia autem partialia characteristica
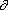 denotare.
denotare.
The "curly d" symbol is sometimes called the "rounded d" or "curved d"
or Jacobi’s delta. It corresponds to the cursive "dey"
(equivalent to our d) in the Cyrillic alphabet.
Integral. Before introducing the integral symbol, Leibniz
wrote omn. for “omnia” in front of the term to be integrated.
The integral symbol was first used by Gottfried Wilhelm Leibniz
(1646-1716) on October 29, 1675, in an unpublished manuscript,
Analyseos tetragonisticae pars secunda:
Utile erit scribi 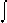 pro omnia, ut
pro omnia, ut 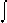 l = omn.
l, id est summa ipsorum l. [It will be useful to write
l = omn.
l, id est summa ipsorum l. [It will be useful to write
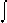 for omn. so
that
for omn. so
that 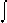 l = omn. l, or the sum of all the
l’s.]
l = omn. l, or the sum of all the
l’s.]
Two weeks later, on Nov. 11, in Methodi tangentium inversae exempla, he first placed dx after the integral symbol, replacing 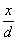
Both manuscripts were first published by Gerhardt. There is now a critical edition (Gottfried Wilhelm Leibniz, Sämtliche Schriften und Briefe, Reihe VII: Mathematische Schriften, vol 5: Infinitesimalmathematik 1674-1676, Berlin : Akademie Verlag, 2008, pp 288-295 and 321-331), online:
http://www.gwlb.de/Leibniz/Leibnizarchiv/Veroeffentlichungen/VII5A.pdf
http://www.gwlb.de/Leibniz/Leibnizarchiv/Veroeffentlichungen/VII5B.pdf
The first appearance of the integral symbol in print
was in a paper by Leibniz in the Acta Eruditorum. The integral
symbol was actually a long letter S for “summa.”
In his Quadratura curvarum of 1704, Newton wrote a small
vertical bar above x to indicate the integral of x. He wrote two
side-by-side vertical bars over x to indicate the integral of (x with
a single bar over it). Another notation he used was to enclose the
term in a rectangle to indicate its integral. Cajori writes that
Newton’s symbolism for integration was defective because the x with a
bar could be misinterpreted as x-prime and the placement of a
rectangle about the term was difficult for the printer, and that
therefore Newton’s symbolism was never popular, even in England.
[Siegmund Probst contributed to this entry.]
Limits of integration. Limits of integration were
first indicated only in words. Euler was the first to use a symbol
in Institutiones calculi integralis, where he wrote the
limits in brackets and used the Latin words ab and ad
(Cajori vol. 2, page 249).
The modern definite integral symbol was originated by Jean
Baptiste Joseph Fourier (1768-1830). In 1822 in his famous The Analytical
Theory of Heat he wrote:
Nous désignons en général par le signe
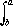 l'intégrale qui commence lorsque la variable équivaut à a, et qui est complète lorsque
la variable équivaut à b. . .
l'intégrale qui commence lorsque la variable équivaut à a, et qui est complète lorsque
la variable équivaut à b. . .
The citation above is from
"Théorie analytique de la chaleur"
[The Analytical Theory of Heat], Firmin Didot, Paris, 1822, page 252 (paragraph 231).
Fourier had used this notation somewhat earlier in the
Mémoires of the French Academy for 1819-20, in an
article of which the early part of his book of 1822 is a reprint
(Cajori vol. 2 page 250).
The bar notation to indicate evaluation of an antiderivative
at the two limits of integration was first used by Pierre Frederic
Sarrus (1798-1861) in 1823 in Gergonne’s Annales, Vol. XIV.
The notation was used later by Moigno and Cauchy (Cajori vol. 2, page
250).
Integration around a closed path. Dan Ruttle, a reader of this page, has found a use of the integral
symbol with a circle in the middle by
Arnold Sommerfeld (1868-1951)
in 1917 in Annalen der
Physik, "Die Drudesche Dispersionstheorie vom Standpunkte des
Bohrschen Modelles und die Konstitution von H2, O2 und N2." This use
is earlier than the 1923 use shown by Cajori. Ruttle reports that J.
W. Gibbs used only the standard integral sign in his Elements of
Vector Analysis (1881-1884), and that and E. B. Wilson used a
small circle below the standard integral symbol to denote integration
around a closed curve in his Vector Analysis (1901, 1909) and
in Advanced Calculus (1911, 1912).
Limit. lim. (with a period) was used first by
Simon-Antoine-Jean L'Huilier (1750-1840).
In 1786, L'Huilier gained
much popularity by winning the prize offered by *l'Academie royale
des Sciences et Belles-Lettres de Berlin*. His essay, "Exposition
élémentaire des principes des calculs superieurs,"
accepted the challenge thrown by the Academy -- a clear and precise
theory on the nature of infinity. On page 31 of this remarkable paper,
L'Huilier states:
Pour abreger & pour faciliter le calcul par une notation
plus commode, on est convenu de désigner autrement que par
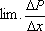 ,
la limite du rapport des changements simultanes de P & de
x, favoir par
,
la limite du rapport des changements simultanes de P & de
x, favoir par
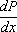 ;
en sorte que
;
en sorte que
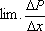 ou
ou
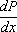 ;
designent la même chose
;
designent la même chose
lim (without a period) was written in 1841 by
Karl Weierstrass
(1815-1897) in one of his papers published in 1894 in
Mathematische Werke, Band I, page 60 (Cajori vol. 2, page 255).
The arrow notation for limits.
In the 1850s, Weierstrass began to use 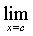 .
.
Our present day expression 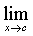 seems to have
originated with the English mathematician John Gaston Leathem in his 1905 book
Volume and Surface Integrals Used in Physics.
seems to have
originated with the English mathematician John Gaston Leathem in his 1905 book
Volume and Surface Integrals Used in Physics.
Leathem wrote the following in his
undated Preface (p. v, paragraph 3) to Elements
of the Mathematical Theory of Limits, G. Bell
and Sons, 1925:
The arrow symbol for tendency
to limit was introduced in my tract on Surface
and Volume Integrals published by the Cambridge
University Press in 1905. It has been erroneously
attributed to another writer owing to its use,
with inadvertent omission of acknowledgment, in
an important book published three years later.
It is now a well-established notation, and I have
thought it desirable to supplement it in the
present work by using sloped arrows to distinguish
upward and downward tendencies.
The widespread use of the arrow notation can probably be attributed to its appearance in two books in 1908:
An Introduction to the Theory of Infinite Series (1st ed.) by Thomas John I'Anson Bromwich and
A Course of Pure Mathematics by Godfrey Harold Hardy. [See pp. 116-118 and 163-164 in Hardy.]
The following comments appear in the Preface of Hardy’s 1908 book (p. ix):

[This entry was contributed by Dave L. Renfro.]
Infinity. The infinity symbol 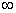 was introduced by
John Wallis (1616-1703)
in 1655 in his De sectionibus conicis (On Conic Sections) as follows:
was introduced by
John Wallis (1616-1703)
in 1655 in his De sectionibus conicis (On Conic Sections) as follows:
Suppono in limine (juxta^ Bonaventurae Cavallerii
Geometriam Indivisibilium) Planum quodlibet quasi ex infinitis
lineis parallelis conflari: Vel potiu\s (quod ego mallem) ex
infinitis Prallelogrammis [sic] aeque\ altis; quorum quidem
singulorum altitudo sit totius altitudinis 1/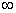 , sive alicuota pars infinite
parva; (esto enim
, sive alicuota pars infinite
parva; (esto enim 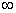 nota numeri infiniti;) adeo/q; omnium simul altitude
aequalis altitudini figurae.
nota numeri infiniti;) adeo/q; omnium simul altitude
aequalis altitudini figurae.
Wallis also used the infinity symbol in various passages of his
Arithmetica infinitorum (Arithmetic of Infinites) (1655 or
1656). For instance, he wrote (p. 70):
Cum enim primus terminus in serie Primanorum sit 0,
primus terminus in serie reciproca erit 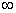 vel infinitus: (sicut, in
divisione, si diviso sit 0, quotiens erit infinitus)
vel infinitus: (sicut, in
divisione, si diviso sit 0, quotiens erit infinitus)
In Zero to Lazy Eight, Alexander Humez, Nicholas Humez, and
Joseph Maguire write: "Wallis was a classical scholar and it is
possible that he derived ![[the infinity symbol]](infinity.gif) from the old Roman sign for 1,000, CD,
also written M--though it is also possible that he got the idea from
the lowercase omega, omega being the last letter of the Greek alphabet
and thus a metaphor of long standing for the upper limit, the
end."
from the old Roman sign for 1,000, CD,
also written M--though it is also possible that he got the idea from
the lowercase omega, omega being the last letter of the Greek alphabet
and thus a metaphor of long standing for the upper limit, the
end."
Cajori (vol. 2, p 44) says the conjecture has been made that Wallis
adopted this symbol from the late Roman symbol 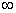 for 1,000. He attributes the
conjecture to Wilhelm Wattenbach (1819-1897),
Anleitung zur lateinischen Paläographie 2. Aufl.,
Leipzig: S. Hirzel, 1872. Appendix: p. 41.
for 1,000. He attributes the
conjecture to Wilhelm Wattenbach (1819-1897),
Anleitung zur lateinischen Paläographie 2. Aufl.,
Leipzig: S. Hirzel, 1872. Appendix: p. 41.
This conjecture is lent credence by the labels inscribed on a Roman
hand abacus stored at the Bibliothèque Nationale in Paris. A
plaster cast of this abacus is shown in a photo on page 305 of the
English translation of Karl Menninger’s Number Words and Number
Symbols; at the time, the cast was held in the Cabinet des
Médailles in Paris. The photo reveals that the column devoted
to 1000 on this abacus is inscribed with a symbol quite close in
shape to the lemniscate symbol, and which Menninger shows would
easily have evolved into the symbol M, the eventual Roman symbol for
1000 [Randy K. Schwartz].
[Julio González Cabillón contributed to this entry.]
Delta to indicate a small quantity. In 1706,
Johann Bernoulli
used δ to denote the difference of functions. Julio González Cabillón believes this
is probably one of the first if not the first use of delta in this sense.
Delta and epsilon. Augustin-Louis Cauchy
(1789-1857) used ε in 1821 in Cours d'analyse
(Oeuvres II.3),
and sometimes used δ instead (Cajori vol. 2, page 256). According to Finney and Thomas (page
113), "δ meant 'différence' (French for difference
and ε meant 'erreur' (French for error)."
The first theorem on limits that Cauchy sets out to prove in the Cours d'Analyse
(Oeuvres II.3, p. 54)
has as hypothesis that
for increasing values of x, the difference f(x + 1) - f(x) converges to a certain limit k.
The proof then begins by saying
denote by ε a number as small as one may wish.
Since the increasing values of x make the difference f(x + 1) - f(x)
converge to the limit k, one can assign a sufficiently substantial
value to a number h so that, for x bigger than or equal to h,
the difference in question is always between the bounds k -
ε, k + ε.
[William C. Waterhouse]
The first delta-epsilon proof is Cauchy’s proof of what is
essentially the mean-value theorem for derivatives. It comes from his lectures
on the Calcul infinitesimal, 1823, Leçon 7, in
Oeuvres, Ser. 2, vol. 4, pp. 44-45.
The proof translates Cauchy’s verbal definition of the derivative as the limit (when it exists) of
the quotient of the differences into the language of algebraic
inequalities using both delta and epsilon. In the 1820s Cauchy did
not specify on what, given an epsilon, his delta or n depended, so
one can read his proofs as holding for all values of the variable.
Thus he does not make the distinction between converging to a limit
pointwise and convering to it uniformly.
[Judith V. Grabiner, author of The Origins of Cauchy’s Rigorous Calculus (MIT, 1981)]
VECTOR CALCULUS SYMBOLS
For vector analysis entries on the Words pages,
see here for a list.
The vector differential operator, now written
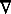 and called nabla or del, was introduced by William Rowan Hamilton
(1805-1865). Hamilton wrote the operator as
and called nabla or del, was introduced by William Rowan Hamilton
(1805-1865). Hamilton wrote the operator as
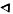 and it was P. G. Tait who established
and it was P. G. Tait who established
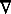 as the conventional symbol--see his An Elementary Treatise on Quaternions
(1867). Tait was also responsible for establishing the term nabla. See
NABLA on the Earliest Uses of Words page.
as the conventional symbol--see his An Elementary Treatise on Quaternions
(1867). Tait was also responsible for establishing the term nabla. See
NABLA on the Earliest Uses of Words page.
David Wilkins suggests that Hamilton may have used the nabla
as a general purpose symbol or abbreviation for whatever operator he wanted
to introduce at any time. In 1837 Hamilton used the nabla, in its modern orientation,
as a symbol for any arbitrary function in Trans. R. Irish Acad. XVII.
236. (OED.) He used the nabla to signify a permutation operator in "On
the Argument of Abel, respecting the Impossibility of expressing a Root of any
General Equation above the Fourth Degree, by any finite Combination of Radicals
and Rational Functions," Transactions of the Royal Irish Academy,
18 (1839), pp. 171-259.
Hamilton used the rotated nabla, i.e.
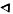 ,
for the vector differential operator in the "Proceedings of the Royal Irish Academy" for the meeting
of July 20, 1846. This paper appeared in volume 3 (1847), pp. 273-292. Hamilton
also used the rotated nabla as the vector differential operator in "On
Quaternions; or on a new System of Imaginaries in Algebra"; which he published
in instalments in the Philosophical Magazine between 1844 and 1850. The
relevant portion of the paper consists of articles 49-50, in the instalment
which appeared in October 1847 in volume 31 (3rd series, 1847) of the Philosophical
Magazine, pp. 278-283. A footnote in vol. 31, page 291, reads:
,
for the vector differential operator in the "Proceedings of the Royal Irish Academy" for the meeting
of July 20, 1846. This paper appeared in volume 3 (1847), pp. 273-292. Hamilton
also used the rotated nabla as the vector differential operator in "On
Quaternions; or on a new System of Imaginaries in Algebra"; which he published
in instalments in the Philosophical Magazine between 1844 and 1850. The
relevant portion of the paper consists of articles 49-50, in the instalment
which appeared in October 1847 in volume 31 (3rd series, 1847) of the Philosophical
Magazine, pp. 278-283. A footnote in vol. 31, page 291, reads:
In that paper designed for Southampton the characteristic was written
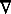 ;
but this more common sign has been so often used with other meanings, that it
seems desirable to abstain from appropriating it to the new signification here
proposed.
;
but this more common sign has been so often used with other meanings, that it
seems desirable to abstain from appropriating it to the new signification here
proposed.
Wilkins writes that "that paper"
refers to an unpublished paper that Hamilton had prepared for a meeting of the
British Association for the Advancement of Science, but which had been forwarded
by mistake to Sir John Herschel’s home address, not to the meeting itself in
Southampton, and which therefore was not communicated at that meeting. The footnote
indicates that Hamilton had originally intended to use the nabla symbol that
is used today but then decided to rotate it to avoid confusion with other uses
of the symbol.
The rotated form appears in Hamilton’s magnum opus, the
Lectures on Quaternions (1853, p. 610).
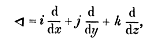
Cajori (vol. 2, page 135) and the OED give this reference.
According to Stein and Barcellos (page 836), Hamilton denoted
the gradient with an ordinary capital delta in 1846. However, this information
may be incorrect, as David Wilkins writes that he has never seen the gradient
denoted by an ordinary capital delta in any paper of Hamilton published in his
lifetime.
David Wilkins of the School of Mathematics at Trinity College in Dublin has made
available texts of the mathematical papers published by Hamilton in his lifetime at his
History of Mathematics website.
grad as a symbol for gradient appears in H. Weber’s Die partiellen differential-gleichungen
der mathematischen physik nach Riemanns Vorlesungen of 1900 (Cajori vol. 2, page 135). See
GRADIENT on the Earliest Uses of Words page.
William Kingdon Clifford (1845-1879) used div u or dv u as symbols for divergence (Cajori vol. 2, page
135).
The symbol Δ for the Laplacian operator (also represented by
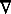 2)
was introduced by Robert Murphy
in 1833 in Elementary Principles of the Theories of Electricity. (Kline, page 786).
See LAPLACE’s OPERATOR on the Earliest Uses of Words page.
2)
was introduced by Robert Murphy
in 1833 in Elementary Principles of the Theories of Electricity. (Kline, page 786).
See LAPLACE’s OPERATOR on the Earliest Uses of Words page.
Front Page |
Operation |
Grouping |
Relation |
Fractions and Decimals |
Constants |
Variables |
Functions |
Geometry |
Trigonometry |
Calculus |
Matrices and Vectors |
Set Theory and Logic |
Number theory |
Statistics |
Sources
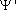 for
for 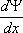 in his memoir
Nouvelle méthode pour résoudre les équations littérales par le moyen des séries
(Oeuvres, Vol. III, pp. 5-76).
The notation also occurs in a memoir by François Daviet de Foncenex in 1759
believed actually to have been written by Lagrange (Cajori 1919, page 256).
in his memoir
Nouvelle méthode pour résoudre les équations littérales par le moyen des séries
(Oeuvres, Vol. III, pp. 5-76).
The notation also occurs in a memoir by François Daviet de Foncenex in 1759
believed actually to have been written by Lagrange (Cajori 1919, page 256).
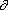 z désigneront ou deux
differences partielles de z,, dont une par rapport a x,
l'autre par rapport a y, ou bien dz sera une
différentielle totale, &
z désigneront ou deux
differences partielles de z,, dont une par rapport a x,
l'autre par rapport a y, ou bien dz sera une
différentielle totale, & 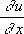 by
Adrien Marie Legendre
in 1786 in his "Memoire sur la manière de distinguer les maxima des minima dans le Calcul des Variations,"
Histoire de l'Academie Royale des Sciences,
Annee M. DCCLXXXVI (1786), pp. 7-37, Paris, M. DCCXXXVIII (1788).
On page 8, it reads:
by
Adrien Marie Legendre
in 1786 in his "Memoire sur la manière de distinguer les maxima des minima dans le Calcul des Variations,"
Histoire de l'Academie Royale des Sciences,
Annee M. DCCLXXXVI (1786), pp. 7-37, Paris, M. DCCXXXVIII (1788).
On page 8, it reads:
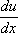 la différence complète de
u divisée par dx.
la différence complète de
u divisée par dx.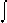 pro omnia, ut
pro omnia, ut 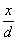
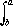 l'intégrale qui commence lorsque la variable équivaut à a, et qui est complète lorsque
la variable équivaut à b. . .
l'intégrale qui commence lorsque la variable équivaut à a, et qui est complète lorsque
la variable équivaut à b. . .
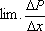 ,
la limite du rapport des changements simultanes de P & de
x, favoir par
,
la limite du rapport des changements simultanes de P & de
x, favoir par
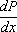 ;
en sorte que
;
en sorte que
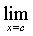 .
.
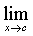 seems to have
originated with the English mathematician John Gaston Leathem in his 1905 book
Volume and Surface Integrals Used in Physics.
seems to have
originated with the English mathematician John Gaston Leathem in his 1905 book
Volume and Surface Integrals Used in Physics.

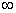 was introduced by
was introduced by
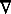 and called nabla or del, was introduced by William Rowan Hamilton
(1805-1865). Hamilton wrote the operator as
and called nabla or del, was introduced by William Rowan Hamilton
(1805-1865). Hamilton wrote the operator as
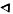 and it was P. G. Tait who established
and it was P. G. Tait who established