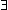 in volume II, number 1, of his Formulaire de
mathematiqués, which was published in 1897, according to Cajori vol. 2,
page 300. However, this document shows
a backwards E with serifs. [Thanks to Ivan Panchenko for noticing this.]
in volume II, number 1, of his Formulaire de
mathematiqués, which was published in 1897, according to Cajori vol. 2,
page 300. However, this document shows
a backwards E with serifs. [Thanks to Ivan Panchenko for noticing this.]Last updated: Oct. 8, 2019
Most of the basic symbols of logic and set theory in use today were introduced between 1880 and 1920. The main contributors were Ernst Schröder (1841-1902), Giuseppe Peano (1858-1932), Alfred North Whitehead (1861-1947) and Bertrand Russell (1872-1970). Peano had a strong influence on Whitehead and Russell and their joint work, Principia Mathematica (1910-1913), was itself very influential. Today Gottlob Frege (1848-1925) is the most admired logician of that age but his notation was not taken up. Most of the symbols described here are treated in the chapter on mathematical logic in Cajori's A History of Mathematical Notations, vol. 2 (1929). The ideas of the period are covered in I. Grattan-Guinness (2000) The Search for Mathematical Roots, 1870-1940: Logics, Set Theories and the Foundations of Mathematics from Cantor through Russell to Gödel. Many of the classic works are available in English in Jan van Heijenoort (1967) From Frege to Gödel: A Source Book in Mathematical Logic, 1879-1931.
For set theory and logic entries on the Words pages, see here for a list.
Intersection and union. The symbols ∩ and ∪ were used by Giuseppe Peano (1858-1932) for intersection and union in 1888 in Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann (Cajori vol. 2, page 298); the logical part of this work with this symbols is ed. in: Peano, opere scelte, 2, Rom 1958, p. 3-19.
Peano also created the large symbols for general intersection and union of more than two classes in 1908. These symbols can be seen in the Wikipedia article on Union (set theory). The source is: G. Peano: Formulario mathematico, tomo V, Torino 1908, Facsimile-Reprint, Rom 1960, p. 82. [This information was provided by Wilfried Neumaier, who reports that Cajori vol. 2 does not have the correct earliest use for these symbols.]
Existence (existential quantifier). Peano used 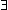 in volume II, number 1, of his Formulaire de
mathematiqués, which was published in 1897, according to Cajori vol. 2,
page 300. However, this document shows
a backwards E with serifs. [Thanks to Ivan Panchenko for noticing this.]
in volume II, number 1, of his Formulaire de
mathematiqués, which was published in 1897, according to Cajori vol. 2,
page 300. However, this document shows
a backwards E with serifs. [Thanks to Ivan Panchenko for noticing this.]
Kevin C. Klement writes, "While Peano had the backwards E for a predicate of classes, Russell was the first to use the backwards E as a variable binding operator, and there are the wonderful manuscripts printed in CPBR vol 4 in which Russell's makes large dots out of Peano's backwards epsilons to change over from the Peano-notation for existence to a more Fregean one."
Membership. Giuseppe Peano (1858-1932) used an epsilon for membership in Arithmetices prinicipia nova methodo exposita, Turin 1889 (page vi, x). He stated that the symbol was an abbreviation for est; the entire work is in Latin. [This citation was contributed by Wilfried Neumaier.]
Peano’s symbol for membership appears to be a lunate (or uncial) epsilon, and not the stylized epsilon  that is now
used. This web page previously stated that the modern stylized epsilon was adopted by Bertrand Russell in Principles of Mathematicsin
1903; however, Russell stated he was using Peano’s symbol, and it
appears also to be a lunate epsilon, and is not intended to be the
modern
symbol.
Peano’s I Principii di geometria logicamente esposti, also 1889, has the more common epsilon ε.
that is now
used. This web page previously stated that the modern stylized epsilon was adopted by Bertrand Russell in Principles of Mathematicsin
1903; however, Russell stated he was using Peano’s symbol, and it
appears also to be a lunate epsilon, and is not intended to be the
modern
symbol.
Peano’s I Principii di geometria logicamente esposti, also 1889, has the more common epsilon ε.
The symbol 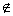 for negated membership was apparently first used in 1939 by Bourbaki, Nicholas, Theorie des ensembles,
Paris, 1939, page 4. [Wilfried Neumaier]
for negated membership was apparently first used in 1939 by Bourbaki, Nicholas, Theorie des ensembles,
Paris, 1939, page 4. [Wilfried Neumaier]
Such that. According to Julio González Cabillón, Peano introduced the backwards lower-case epsilon for "such that" in "Formulaire de Mathematiques vol. II, #2" (p. iv, 1898).
Peano introduced the backwards lower-case epsilon for "such that" in his 1889 "Principles of arithmetic, presented by a new method," according van Heijenoort's From Frege to Gödel: A Source Book in Mathematical Logic, 1879--1931 [Judy Green].
For all. According to M. J. Cresswell and Irving H. Anellis,
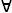 originated in
Gerhard Gentzen,
"Untersuchungen ueber das logische Schliessen,"
Math. Z., 39,
(1935), p, 178. In footnote 4 on that page, Gentzen explains how he came to use the sign. It
is the "All-Zeichen," an analogy with
originated in
Gerhard Gentzen,
"Untersuchungen ueber das logische Schliessen,"
Math. Z., 39,
(1935), p, 178. In footnote 4 on that page, Gentzen explains how he came to use the sign. It
is the "All-Zeichen," an analogy with
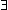 for the existential quantifier which Gentzen says that he borrowed from Russell.
for the existential quantifier which Gentzen says that he borrowed from Russell.
Russell used the notation (x) for "for all x". See his "Mathematical Logic as Based on the Theory of Types," American Journal of Mathematics, 30, (1908), 222-262. [Denis Roegel].
Braces enclosing the elements of a set. The symbol {a} for a set with only one Element and {a, b} for a set with two Elements in the modern sense introduced by Ernst Zermelo 1907 in “Untersuchungen über die Grundlagen der Mengenlehre,” Mathematische Annalen 65 (1908), page 263. Georg Cantor used the set brackets {a, b},..., {a, b, ....} earlier in 1878 in “Ein Beitrag zur Mannifaltigkeitslehre” in Crelles Journal für Mathematik, 84 (1878), p. 242-258, however in another meaning: here {a,b} not a set with two Elements, but the disjoint union of the sets a and b. Another meaning has also {m} in his Definition of set:
Unter einer 'Menge' verstehen wir jede Zusammenfassung M von bestimmten wohlunterschiedenen Objecten m unsrer Anschauung oder unseres Denkens (welche die 'Elemente' von M genannt werden) zu einem Ganzen.In Zeichen druecken wir dies so aus:
M = {m}.
M is here the symbol for any set, not for a set with only one Element. The equation M = {m} means M={m|m M} based on the verbal text in brackets of the Definition.
The citation above is from "Beiträge zur Begründung der transfiniten Mengenlehre" [Contributions to the founding of the theory of transfinite numbers], Mathematische Annalen, Band XLVI [vol. 46], pp. 481-512, B. G. Teubner, Leipzig, 1895. Please recall that Cantor's "Contributions to the founding of the theory of transfinite numbers" [first published by The Open Court publishing Company, Chicago-London, 1915] is a translation of the two memoirs which had appeared in Mathematische Annalen for 1895 and 1897 under the title: "Beiträge zur Begründung der transfiniten Mengenlehre" -- translation from the German, introduction, and notes by Philip Edward Bertrand Jourdain (1879-1919). An unabridged and unaltered republication of the English translation mentioned was edited also by Dover Publications, Inc., New York, 1955 [ISBN: 0486600459].
M stands for the German term "Menge." Cantor may have used this notation earlier in his correspondence with the mathematicians of his day. (This entry was contributed by Julio González Cabillón.)
p is used for propositions in 1897 in Peano's "Studii di logica matematica," according to Kevin C. Klement.
p, q, and r were used as propositional letters by Bertrand Russell in 1903 in The Principles of Mathematics (OED).
Negation. The tilde ~ for negation was used by Peano in 1897. See Peano, “Studii di logica matematica,” ed. in: Peano, opere scelte, 2, Rom 1958, p. 212. [Kevin C. Klement]
~p for "the negation of p" appears in 1908 in the article "Mathematical logic as based on the theory of types" by Bertrand Russell [Denis Roegel].
The symbolism was also used in 1910 by Alfred North Whitehead and Bertrand Russell in the first volume of Principia mathematica (Cajori vol. 2, page 307).
The main symbol for negation wich is used today is ¬. It was first used in 1930 by Arend Heyting in “Die formalen Regeln der intuitionistischen Logik,” Sitzungsberichte der preußischen Akademie der Wissenschaften, phys.-math. Klasse, 1930, p. 42-65. The ¬ appears on p. 43. [Wilfried Neumaier]
Disjunction. ∨ for disjunction is found in Russell's manuscripts from 1902-1903 and in 1906 in Russell's paper "The Theory of Implication," in American Journal of Mathematics vol. 28, pp. 159-202, according to Kevin C. Klement.
p \/ q for "p or q" appears in 1908 in the article (1908) "Mathematical Logic as Based on the Theory of Types," American Journal of Mathematics, 30, 222-262. by Bertrand Russell [Denis Roegel].
The symbolism was also used in 1910 by Alfred North Whitehead and Bertrand Russell in the first volume of Principia mathematica. (These authors used p.q for "p and q.") (Cajori vol. 2, page 307)
Conjunction. The symbol ∧ for logical conjunction "and" was first used in 1930 by Arend Heyting in the same source as shown for the negation symbol above. [Wilfried Neumaier]
Implication. The arrow symbol → for the logical implication was first used in 1922 by David Hilbert in: Hilbert: Neubegründung der Mathematik, 1922, in: Abhandlungen aus dem Mathematischen Seminar der Hamburger Universität, Band I (1922), 157-177. The symbol is found on p. 166. [Wilfried Neumaier]
The arrow with double lines ⇒ was first used 1954 by Nicholas Bourbaki, in: Bourbaki: Theorie des ensembles, 3. edition, Paris, 1954. The symbol appears on p. 14. [Wilfried Neumaier]
Equivalence. The double arrow symbol ↔ for the logical equivalence was apparently first used in 1933 by Albrecht Becker Die Aristotelische Theorie der Möglichkeitsschlüsse, Berlin, 1933, page 4. [Wilfried Neumaier]
The double arrow with double line ⇔ was first used 1954 by Nicholas Bourbaki, in: Bourbaki: Theorie des ensembles, 3. edition, Paris, 1954. The symbol appears on p. 32. [Wilfried Neumaier]
The null set symbol (Ø) first appeared in N. Bourbaki Éléments de mathématique Fasc.1: Les structures fondamentales de l'analyse; Liv.1: Theorie de ensembles. (Fascicule de resultants) (1939): "certaines propriétés... ne sont vraies pour aucun élément de E... la partie qu’elles définissent est appelée la partie vide de E, et designée par la notation Ø." (p. 4.)
André Weil (1906-1998) says in his autobiography that he was responsible for the symbol:
Wisely, we had decided to publish an installment establishing the system of notation for set theory, rather than wait for the detailed treatment that was to follow: it was high time to fix these notations once and for all, and indeed the ones we proposed, which introduced a number of modifications to the notations previously in use, met with general approval. Much later, my own part in these discussions earned me the respect of my daughter Nicolette, when she learned the symbol Ø for the empty set at school and I told her that I had been personally responsible for its adoption. The symbol came from the Norwegian alphabet, with which I alone among the Bourbaki group was familiar.The citation above is from page 114 of André Weil's The Apprenticeship of a Mathematician, Birkhaeuser Verlag, Basel-Boston-Berlin, 1992. Translated from the French by Jennifer Gage. The citation was provided by Julio González Cabillón.
This letter is used in the Norwegian, Danish and Faroese alphabets.
The "therefore" symbol ( )was first published in 1659 in the
original German edition of Teusche Algebra by Johann Rahn
(1622-1676) (Cajori vol. 1, page 212, and vol 2., page 282).
)was first published in 1659 in the
original German edition of Teusche Algebra by Johann Rahn
(1622-1676) (Cajori vol. 1, page 212, and vol 2., page 282).
The "because" symbol ( ).
Cajori writes, "We have not been able to find the use of
).
Cajori writes, "We have not been able to find the use of  for 'because' in
the eighteenth century. This usage seems to have been introduced in Great Britain and the United States
in the nineteenth century. It is found in the Gentleman's Mathematical Companion (1805). It did not
meet with as wide acceptance in Great Britain and America as did
for 'because' in
the eighteenth century. This usage seems to have been introduced in Great Britain and the United States
in the nineteenth century. It is found in the Gentleman's Mathematical Companion (1805). It did not
meet with as wide acceptance in Great Britain and America as did  for 'therefore'"
(pages 282-283).
for 'therefore'"
(pages 282-283).
The halmos (a box indicating the end of a proof). In his Measure Theory (1950, p. 6) P. R. Halmos writes, “The symbol▐ is used throughout the entire book in place of such phrases as “Q.E.D.” or “This completes the proof of the theorem” to signal the end of a proof.”
On the last page of his autobiography, Paul R. Halmos writes:
My most nearly immortal contributions are an abbreviation and a typographical symbol. I invented “iff”, for “if and only if”—but I could never believe that I was really its first inventor. I am quite prepared to believe that it existed before me, but I don't know that it did, and my invention (re-invention?) of it is what spread it thorugh the mathematical world. The symbol is definitely not my invention—it appeared in popular magazines (not mathematical ones) before I adopted it, but, once again, I seem to have introduced it into mathematics. It is the symbol that sometimes looks like, and is used to indicate an end, usually the end of a proof. It is most frequently called the “tombstone”, but at least one generous author referred to it as the “halmos”.
This quote is from I Want to Be a Mathematician: An Automathography, by Paul R. Halmos, Springer-Verlag, New York, Berlin, Heidelberg, Tokyo, 1985, page 403. Thanks to Alexander Brandt for assisting with this entry.
See the entry Q. E. D. on Earliest Known Uses of Some of the Words of Mathematics (Q).
The aleph null symbol was conceived by Georg Cantor (1845-1918) around 1893, and became widely known after "Beiträge zur Begründung der transfiniten Mengenlehre" [Contributions to the Foundation of Transfinite Set Theory] saw the light in Mathematische Annalen, Band XLVI [vol. 46], B. G. Teubner, Leipzig, 1895.
On page 492 of this prestigious journal we find the paragraph Die kleinste transfinite Cardinalzahl Alef-null [The minimum transfinite cardinal number Aleph null], and the following:
...wir nennen die ihr zukommende Cardinalzahl, in Zeichen,... [We call the cardinal number related to that (set); in symbol,
]
In a letter dated April 30, 1895, Cantor wrote, "it seemed to me that for this purpose, other alphabets were [already] over-used" (translation by Martin Davis).
In Georg Cantor, Dauben (page 179) says that Cantor did not want to use Roman or Greek alphabets, because they were already widely used, and "His new numbers deserved something unique. ... Not wishing to invent a new symbol himself, he chose the aleph, the first letter of the Hebrew alphabet...the aleph could be taken to represent new beginnings...." Avinoam Mann points out that aleph is also the first letter of the Hebrew word "Einsof," which means infinity and that the Kabbalists use "einsof" for the Godhead.
Although his father was a Lutheran and his mother was a Roman Catholic, Cantor had at least some Jewish ancestry.
(Julio González Cabillón. contributed to this entry.)
Set inclusion. According to Cajori (vol. 2, page 294), the symbols
![]() for "is included in" (untergeordnet) and
for "is included in" (untergeordnet) and
![]() for "includes" (übergeordnet)
were introduced by Schröder Vorlesungen über die Algebra der Logik vol. 1 (1890). Previously the symbols < and > had been used.
for "includes" (übergeordnet)
were introduced by Schröder Vorlesungen über die Algebra der Logik vol. 1 (1890). Previously the symbols < and > had been used.
According to a web page by Paul Taylor, "Joseph Gergonne introduced C for contient and É for its converse in 1817, and these symbols were used by Peano and by Russell and Whitehead. (In fact Russell and Whitehead also used Ì for containment in our sense.)"
According W. V. Quine, Methods of Logic, 4th ed., Harvard University Press, 1982, page 132:
“The inclusion signs 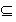 and
and 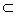 , now current in set theory,
are derived from Gergonne's use in 1816 of 'C' for containment.” In the bibliography he lists the following:
Gergonne, J. D. “Essai de dialectique rationelle.” Annales de mathématiques pure et appliquées,
vol. 7 (1816-17), pp. 189-228. [Susanna Epp]
, now current in set theory,
are derived from Gergonne's use in 1816 of 'C' for containment.” In the bibliography he lists the following:
Gergonne, J. D. “Essai de dialectique rationelle.” Annales de mathématiques pure et appliquées,
vol. 7 (1816-17), pp. 189-228. [Susanna Epp]
Equal by definition. =Def is found in C. Burali-Forti Logicamatematica (1894) (Grattan-Guinness (2000) p. 216).
Double turnstile. The double turnstile 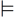 is found in
“Ultraproducts in the Theory of Models,” by Simon Kochen, Annals of
Mathematics, v.74, 1961, pp 221-261, where the writer defines and makes extensive
use of it. Kochen wrote to the Foundations of Mathematics email list in 2017, “The paper is based on my 1959 Ph.D. thesis in Princeton,
which also uses the double turnstile. I cannot recollect whether I
originated it or took it from some other paper.”
According to a message in FOM by Neil Tennant, “Professor Kochen’s 1961 paper in the Annals of Mathematics uses the
double turnstile for the relation between a model and a sentence that it
makes true.”
is found in
“Ultraproducts in the Theory of Models,” by Simon Kochen, Annals of
Mathematics, v.74, 1961, pp 221-261, where the writer defines and makes extensive
use of it. Kochen wrote to the Foundations of Mathematics email list in 2017, “The paper is based on my 1959 Ph.D. thesis in Princeton,
which also uses the double turnstile. I cannot recollect whether I
originated it or took it from some other paper.”
According to a message in FOM by Neil Tennant, “Professor Kochen’s 1961 paper in the Annals of Mathematics uses the
double turnstile for the relation between a model and a sentence that it
makes true.”
The use of the double turnstile for logical consequence started a bit later, probably around 1963 but surely in 1967, as stated here.