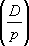 = 1 if D is a quadratic residue of p, and
= 1 if D is a quadratic residue of p, and
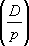 = -1 if D is a quadratic non-residue of p.
= -1 if D is a quadratic non-residue of p.
Divisibility. In the unpublished notes of his 1925 number theory seminar, Hardy used a|b several times in reference to work by Polya. [Jim Tattersall]
In 1927 Edmund Landau used a|b in Elementary Number Theory. [Jim Tattersall]
Congruence of numbers. The congruent symbol used in number theory ≡ was introduced in print in 1801 by Carl Friedrich Gauss (1777-1855) in Disquisitiones arithmeticae:
Numerorum congruentiam hoc signo, ≡, in posterum denotabimus, modulum ubi opus erit in clausulis adiungentes, -16 ≡ 9 (mod. 5), -7 ≡ 15 (mod. 11).The citation above is from Disquisitiones arithmeticae (Leipzig, 1801), art. 2; Werke, Vol. I (Gottingen, 1863), p. 10 (Cajori vol. 2, page 35).
However, Gauss had used the symbol much earlier in his personal writings (Francis, page 82).
See MODULUS on Words page.
The number of primes less than x. Edmund Landau used π(x) for the number of primes less than or equal to x in 1909 in Handbuch der Lehre von der Verteilung der Primzahlen (Cajori vol. 2, page 36).
Letters for the sets of rational and real numbers. The authors of classical textbooks such as Weber and Fricke did not denote particular domains of computation with letters.
In 1872 Richard Dedekind denoted the rationals by R and the reals by blackletter R in Stetigkeit und irrationale Zahlen (1872) (Continuity and irrational numbers Works, 3, 315-334. Dedekind also used K for the integers and J for complex numbers.
In 1888 Richard Dedekind denoted the natural numbers by N in Was ist und was sollen die Zahlen, §6.
In 1889 Giuseppe Peano cited Dedekind’s book in his Arithmetices prinicipia nova methodo exposita, and used the same symbol for the positive integers as Dedekind. Peano used N, R, and Q, and showed their meaning in a table on page 23:
| N | numerus integer positivus |
| R | num. rationalis positivus |
| Q | quantitas, sive numerus realis positivus |
In 1895 in his Formulaire de mathématiques, Peano used N for the positive integers, n for integers, N0 for the positive integers and zero, R for positive rational numbers, r for rational numbers, Q for positive real numbers, q for real numbers, and Q0 for positive real numbers and zero [Cajori vol. 2, page 299].
In 1897 Peano used N1 instead of N. [Wilfried Neumaier]
In 1926 Helmut Hasse (1898-1979) used Γ for the integers and Ρ (capital rho) for the rationals in Höhere Algebra I and II, Berlin 1926. He kept to this notation in his later books on number theory. Hasse's choice of gamma and rho may have been determined by the initial letters of the German terms "ganze Zahl" (integer) and "rationale Zahl" (rational).
In 1929 Otto Haupt used G0 for the integers and Ρ0 (capital rho) for the rationals in Einführung in die Algebra I and II, Leipzig 1929.
In 1930 Bartel Leendert van der Waerden used C for the integers and Γ for the rationals in Moderne Algebra I, Berlin 1930, but in editions during the sixties, he changed to Z and Q.
In 1930 Edmund Landau denoted the set of integers by a fraktur Z with a bar over it in Grundlagen der Analysis (1930, p. 64). He does not seem to introduce symbols for the sets of rationals, reals, or complex numbers.
Q for the set of rational numbers and Z for the set of integers are apparently due to N. Bourbaki. (N. Bourbaki was a group of mostly French mathematicians which began meeting in the 1930s, aiming to write a thorough unified account of all mathematics.) The letters stand for the German Quotient and Zahlen. These notations occur in Bourbaki's Algébre, Chapter 1.
Julio González Cabillón writes that he believes Bourbaki was responsible for both of the above symbols, quoting Weil, who wrote, "...it was high time to fix these notations once and for all, and indeed the ones we proposed, which introduced a number of modifications to the notations previously in use, met with general approval."
[Walter Felscher, Stacy Langton, Peter Flor, Wilfried Neumaier, and A. J. Franco de Oliveira contributed to this entry.]
C for the set of complex numbers. William C. Waterhouse wrote to a history of mathematics mailing list in 2001:
Checking things I have available, I found C used for the complex numbers in an early paper by Nathan Jacobson:Structure and Automorphisms of Semi-Simple Lie Groups in the Large, Annals of Math. 40 (1939), 755-763.The second edition of Birkhoff and MacLane, Survey of Modern Algebra (1953), also uses C (but is not using the Bourbaki system: it has J for integers, R for rationals, R^# for reals). I have't seen the first edition (1941), but I would expect to find C used there too. I'm sure I remember C used in this sense in a number of other American books published around 1950.I think the first Bourbaki volume published was the results summary on set theory, in 1939, and it does not contain any symbol for the complex numbers. Of course Bourbaki had probably chosen the symbols by that time, but I think in fact the first appearance of (bold-face) C in Bourbaki was in the formal introduction of complex numbers in Chapter 8 of the topology book (first published in 1947).
Euler's phi function (totient function). The symbol φ(m) for the number of integers less than m that are relatively prime to m was introduced by Carl Friedrich Gauss (1777-1855) in 1801 in his Disquisitiones arithmeticae articles 38, 39 (p. 30) (Cajori vol. 2, page 35, and Dickson, page 113-115).
The function was first studied by Leonhard Euler (1707-1783), although Dickson (page 113) and Cajori (vol. 2, p. 35) say that Euler did not use a functional notation in Novi Comm. Ac. petrop., 8, 1760-1, 74, and Comm. Arith., 1, 274, and that Euler used πN in Acta Ac. Petrop., 4 II (or 8), 1780 (1755), 18, and Comm. Arith., 2, 127-133. Shapiro agrees, writing: "He did not employ any symbol for the function until 1780, when he used the notation πn."
Sylvester, who introduced the name totient for the function, seems to have believed that Euler had used φ. He writes in 1888 ( vol. IV p. 589 of his Collected Mathematical Papers) "I am in the habit of representing the totient of n by the symbol τ n, τ (taken from the initial of the word it denotes) being a less hackneyed letter than Euler's φ, which has no claim to preference over any other letter of the Greek alphabet, but rather the reverse." This information was taken from a post in sci.math by Robert Israel.
See TOTIENT on Words page.
Legendre symbol (quadratic reciprocity).
Adrien-Marie Legendre introduced the notation
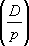 = 1 if D is a quadratic residue of p, and
= 1 if D is a quadratic residue of p, and
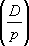 = -1 if D is a quadratic non-residue of p.
= -1 if D is a quadratic non-residue of p.
According to Hardy & Wright's An Introduction to the Theory of Numbers, "Legendre introduced 'Legendre's symbol' in his Essai sur la theorie des nombres, first published in 1798. See, for example, §135 of the second edition (1808)." In the third edition on Gallica this is on p.197.
However, according to William J. Leveque in Fundamentals of Number Theory, "Legendre introduced his symbol in an article in 1785, and at the same time stated the reciprocity law without using the symbol."
[Both of these citations were provided by Paul Pollack.]
Mersenne numbers. Mersenne numbers are marked Mn by Allan Cunningham in 1911 in Mathematical Questions and Solutions from the Educational Times (Cajori vol. 2, page 41).
Fermat numbers. Fermat numbers are marked Fn in 1919 in L. E. Dickson's History of the Theory of Numbers (Cajori vol. 2, page 42).
The norm of a + bi. Dirichlet used N(a+bi) for the norm a2+b2 of the complex number a+bi in Crelle's Journal Vol. XXIV (1842) (Cajori vol. 2, page 33). See NORM on Words page
Galois field. Eliakim Hastings Moore used the symbol GF[qn] to represent the Galois field of order qn in 1893. The modern notation is "Galois-field of order qn" (Julio González Cabillón and Cajori vol. 2, page 41).
Sum of the divisors of n. Euler introduced the symbol
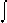 n in a paper published in 1750 (DSB, article:
"Euler").
n in a paper published in 1750 (DSB, article:
"Euler").
In 1888, James Joseph Sylvester continued the use of Euler's notation
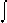 n (Shapiro).
n (Shapiro).
Allan Cunningham used σ(N) to represent the sum of the proper divisors of N in Proceedings of the London Mathematical Society 35 (1902-03):
The Repetition of the Sum-Factor Operation. Abstract of an informal communication made by Lieut.-Col. A. Cuningham, June 12th, 1902.[Cajori, vol. 2, page 29, and Paul Pollack]Let σ(N) denote the sum of the sub-factors of N (including 1, but excluding N). It was found that, with most numbers, σnN = 1, when the operation (σ) is repeated often enough. There is a small class for which σnN = P (a perfect number), and then repeats; another small class for which σnN = A, σn + 1N = B, where A, B are amicable numbers, and then repeats (A, B alternately); another small class for which (even when N is small, < 1000) σnN increases beyond the practical power of calculation.
In 1927 Landau chose the notation S(n) (Shapiro).
L. E. Dickson used s(n) for the sum of the divisors of n (Cajori vol. 2, page 29).
The Möbius function. Möbius' work appeared in 1832 but the µ symbol was not used.
The notation µ(n) was introduced by Franz Mertens (1840-1927) in 1874 in "Über einige asymptotische Gesetze der Zahlentheorie," Crelle's Journal (Shapiro).
Big-O and little-o notation. According to Wladyslaw Narkiewicz in The Development of Prime Number Theory:
The symbols O(·) and o(·) are usually called the Landau symbols. This name is only partially correct, since it seems that the first of them appeared first in the second volume of P. Bachmann's treatise on number theory (Bachmann, 1894). In any case Landau (1909a, p. 883) states that he had seen it for the first time in Bachmann's book. The symbol o(·) appears first in Landau (1909a). Earlier this relation has been usually denoted by {·}.The references are to Paul Bachmann (1837-1920) and his Analytische Zahlentheorie and to Edmund Landau (1877-1938) and his Handbuch der Lehre von der Verteilung der Primzahlen.
[Paul Pollack contributed to this entry.]