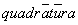meant a division of land into squares.
Last revision: July 7, 2017
Q. E. D. In the Elements Euclid concluded his proofs with ὅπερ ἔδει δεῖξαι “that which was to be shown”: see e.g. the end of the proof of Proposition 4 on p. 11 of Fitzpatrick’s Greek-English Euclid. Medieval geometers translated the expression as quod erat demonstrandum (“that which was to be proven”).
According to Veronika Oberparleiter, the earliest known use in print of the phrase quod erat demonstrandum in a Euclid translation appears in the translation by Bartholemew Zamberti published in Venice in 1505.
In Dialogues Concerning Two New Sciences (1638) in Latin Galileo used quod erat intentum, quod erat demonstrandum, quod erat probandum, quod erat ostendendum, quod erat faciendum, quod erat determinandum, and quod erat propositum.
In 1665 Benedictus de Spinoza (1632-1677) wrote a treatise on ethics, Ethica More Geometrico Demonstrata, in which he proved various moral propositions in a geometric manner. He wrote the abbreviation Q. E. D., as a seal upon his proof of each ethical proposition.
Isaac Barrow used quod erat demonstrandum, quod erat faciendum (Q. E. F.), quod fieri nequit (Q. F. N.), and quod est absurdum (Q. E. A.).
Isaac Newton used the abbreviation Q. E. D.
[Martin Ostwald, Sam Kutler, Robin Hartshorne, David Reed]
See halmos (end of proof sign) on Earliest Uses of Symbols of Set Theory and Logic.
QR ALGORITHM. “The QR algorithm is currently the most popular method for calculating the complete set of eigenvalues of a full (i.e. small) matrix” writes D. S. Watkins “Understanding the QR Algorithm,” SIAM Review, 24, (1982), p. 427. Watkins attributes the method to J. G. F. Francis “The QR transformation I,” Comput. J., 4, (1961), 265-271 and V. N. Kublanovskaya “On Some Algorithms for the Solution of the Complete Eignevalue Problem,” USSR Comput. Math. Phys., 3. 637-657.
QUADRANGLE is found in the geometry sense in English in about 1398 in a translation of Bartholomaeus Anglicus’ De Proprietatibus Rerum. [OED]
The word was used by Shakespeare, in the sense of a rectangular space or courtyard.
QUADRANT, as one fourth of a circle, is found in 1571 in Pantometria by Digges: "Biv, A Quadrant is the fourth part of a Circle, included with two Semidiameters" (OED).
In 1810 Trigonometry, Plane and Spherical; with The Construction and Application of Logarithms by Thomas Simpson has: "The difference of any arch from 90 degrees (or a quadrant) is called its compliment; and its difference from 180 degrees (or a semicircle) its supplement." [Ryan M. Castle]
In 1849, Trigonometry and Double Algebra by August de Morgan has: "The Axes divide the plane into four quarters: and as a line, revolving positively, passes from 0 to 90°, from 90° to 180°, from 180° to 270° , and from 270° to 360°, it is said to be in the first, second, third, and fourth quarters of space. But these might equally well be designated as the ++, +-, --, and -+ quarters of space." [Pat Ballew]
In 1895, Plane and Spherical Trigonometry, Surveying, and Tables by George A Wentworth has: "Let, also, the four quadrants into which the circle is divided by the horizontal and vertical diameters, A A’s, and B B’s, be numbered I, II, III, IV, in the direction of motion." [Pat Ballew, Univ. of Mich. Digital Library]
QUADRATFREI. See the entry SQUAREFREE or SQUARE-FREE.QUADRATIC is derived from the Latin quadratus, meaning "square." In English, quadratic was used in 1668 by John Wilkins (1614-1672) in An essay towards a real character, and a philosophical language [London: Printed for Sa. Gellibrand, and for John Martyn, 1668]. He wrote: "Those Algebraical notions of Absolute, Lineary, Quadratic, Cubic" (OED2)
In his Liber abbaci, Fibonacci referred to problems involving quadratic equations as questiones secundum modum algebre.
QUADRATIC FORM. The term form perhaps in this sense was used by Euler in “Novae demonstrations circa divisors numerorum formae xx _ nyy” which was read Nov. 20, 1775 at the St. Petersburg Academy and published after his death in Nova acta acad. Petrop. I [1783], 1747 47-74. This paper is cited in Disquisitiones Arithmeticae, article 151, page 104.
pq(pp –qq), rt (rr – ss)
fiat quadratum , hic vero casus manifesto ad problema fatis notum deducitur , quo duo triangula rectangula in numeris quarruntur , quorum arese fint inter fe sequales ; quaeruntur igitur duo numeri , uterque formae xy (x x — y y) quorum productum fit quadratum , unde in aequenti Tabella simpliciores numeros huins formae exhibeamus per factores expressos, ubi quidem factores quadratos omittamus:
In hac sectione imprimis de functionibus duarum indeterminatarum x, y, huius formae
axx + 2bxy + cyy ubi a, b, c sunt integri dati, tractabimus, quas formas secundi gradus sive simpliciter formas dicemus.
A translation is: “In this section we shall treat particularly of functions in two unknowns x, y of the form axx + 2bxy + cyy where a, b, c are given integers. We will call these functions forms of the second degree or simply forms.”
Gauss also used Latin terms which are translated binary, ternary, and quaternary forms.
A Google print search finds der binaren quadratischen Formen in a letter dated July 9, 1831, which may have been written by Gauss.
Some other uses in German of quadratic form can be found using Google print search, but these seem to refer to the term as it is used elsewhere in number theory or in chemistry.
Quadratic form is found in English in 1859 in G. Salmon, Less. Mod. Higher Alg.: "A quadratic form can be reduced in an infinity of ways to a sum of squares, yet the number of positive and negative squares in this sum is fixed" (OED2).
Binary quadratic form is found in English in 1861 in “Report on the Theory of Numbers—Part III” by H. J. Stephen Smith [Google print search].
[James A. Landau]
The term QUADRATIC RESIDUE was introduced by Euler in a paper of 1754-55 (Kline, page 611). The term non-residue is found in a paper by Euler of 1758-59, but may occur earlier.
QUADRATRIX. The quadratrix of Hippias was probably invented by Hippias but it became known as a quadratrix when Dinostratus used it for the quadrature of a circle (DSB, article: "Dinostratus"; Webster’s New International Dictionary, 1909).
The term QUADRATRIX OF HIPPIAS was used by Proclus (DSB, article: "Dinostratus").
The quadratrix of Hippias is the first named curve other than circle and line, according to Xah Lee’s Visual Dictionary of Special Plane Curves website.
QUADRATURE, QUADRATURE OF THE CIRCLE, and MECHANICAL QUADRATURE. The OED defines quadrature as the “process of constructing geometrically a square equal in area to that of a given figure, esp. a circle. More widely: the calculation of the area bounded by, or lying under, a curve; the calculation of a definite integral, esp. by numerical methods.”
The problem of squaring the circle was one of classical problems of Greek mathematics: see the MacTutor article
Squaring
the circle. The word quadrature appears in English in the 16th century: the earliest quotation in
the OED is from 1569 in Sanford’s translation of the
contemporary Latin work by Heinrich Corelius Agrippa Of the vanitie and uncertaintie of artes and sciences,
“Yet no Geometrician hath founde out the true
Quadrature [L. quadraturam] of the Circle.” In classical Latin the word
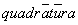meant a division of land into squares.
Agrippa’s book was not a mathematics book and the problem of the quadrature of the circle was well-known outside specialist mathematical circles: the OED’s earliest quotation using the phrase to square the circle is from a 1624 sermon by John Donne (1572-1631): “Goe not Thou about to Square eyther circle [sc. God or thyself].”
Other quotations in the OED illustrate the quadrature of other curves and the connection with CALCULUS: “A method for the Quadrature of Parabola’s of all degrees” from an obituary of Fermat in Philosophical Transactions (1665-1678), 1, (1665 - 1666), 15-16 and “Drawing Tangents to Curves, finding their Curvatures, their Lengths, and Quadratures” from W. Emerson’s The Doctrine of Fluxions 1743.
The term mechanical quadrature is found in German in F. G. Mehler, “Bemerkungen zur Theorie der mechanischen Quadraturen,” J. Reine angew. Math 63 (1864) 152-157. By the early 20th century the term was established in the English mathematical literature. A JSTOR search found G. D. Birkhoff’s “General Mean Value and Remainder Theorems with Applications to Mechanical Differentiation and Quadrature,” Transactions of the American Mathematical Society, 7, 1906), 107-136. The methods of quadrature considered by Birkhoff went back to the early 18th century—one was due to Roger Cotes.
Mechanical quadrature did not usually involve a machine of any kind and in the 20th century the term gave way to numerical quadrature and finally to numerical integration. There is an early appearance of the latter term in the title A Course in Integration and Numerical Integration (1915) by David Gibb. The term is used in the well-known book of 1924, The Calculus of Observations by E. T. Whittaker & G. Robinson. In the course of the 19th century mechanical integrating machines or integrators were developed by physicists. One is described in James Thomson’s “On an Integrating Machine Having a New Kinematic Principle,” Proceedings of the Royal Society of London, 24, (1875 - 1876), 262-265. The history of these machines is related in “Integrators and Planimeters,” chapter 5 of H. H. Goldstine The Computer from Pascal to von Neumann.
QUADRILATERAL appears in English in 1650 in Thomas Rudd’s translation of Euclid.
See also quadrangle.
QUADRIVARIATE is found in J. A. McFadden, "An approximation for the symmetric, quadrivariate normal integral," Biometrika 43, 206-207 (1956).
The QUADRIVIUM of the European Middle Ages consisted of the four mathematical sciences, arithmetic, geometry, astronomy and music. (According to T. L. Heath A History of Greek Mathematics, vol. 1 p. 12, the Pythagoreans divided MATHEMATICS in the same way.) The term was used by the Roman scholar Boethius in his Arithmetica and, according to the DSB, this is “probably the first time the word was used.” Boethius had a profound influence on education in medieval Europe. Preceding the quadrivium in the syllabus was the trivium, for which see the entry LOGIC. The word trivium is echoed in the modern word TRIVIAL.
QUALITY CONTROL. In 1929 W. A. Shewhart gave an address to a meeting of the American Association for the Advancement of Science on "Quality control of the manufactured article." In 1930 Bell Telephone Labs. issued Shewhart’s "Economic quality control of manufactured product". This 26 page pamphlet was followed the next year by a 501 page book Economic Control of Quality of Manufactured Product. (JSTOR search)
The term QUANTIC for a homogeneous function of two or more variables with constant coefficients was introduced by Arthur Cayley in “An Introductory Memoir on Quantics,” Philosophical Transactions of the Royal Society of London, 144 (1854). See Collected Papers II p. 221.
QUANTIFIER (logic.) According to A. Church Introduction to Mathematical Logic (1956, p. 288), "The notion of propositional function and the use of quantifiers, originated with Frege in his Begriffsschrift of 1879... The terms ‘quantifier’ and ‘quantification’ are Peirce’s." In 1885 C. S. Peirce wrote, "If the quantifying part, or Quantifier, contains Σx and we wish to replace the x by a new index i, not already in the Quantifier, and such that every x is an i, we can do so at once by simply multiplying every letter of the Boolian having x as an index by xi." Coll. Papers (1933) III. xiii. P. 232 (OED)
The terms universal quantifier and existential quantifier became established in the 1930s. The OED gives a reference to Łukasiewicz and Tarski writing in Polish in 1930. A JSTOR search found universal quantifier in H. B. Curry "The Universal Quantifier in Combinatory Logic," Annals of Mathematics, 32, (1931), 154-180 and existential quantifier in H. B. Curry "Apparent Variables From the Standpoint of Combinatory Logic," Annals of Mathematics, 34, (1933), 381-404.
For the symbols and for references to the work of Peano and Russell, see the Earliest Use of Symbols page.
QUANTILE as a general term covering quartiles, percentiles, etc. arrived about 60 years after the terms it was generalising.
David (2001) gives M. G. Kendall’s "Note on the Distribution of Quantiles for Large Samples," Supplement to the Journal of the Royal Statistical Society, 7, (1940 - 1941), 83-85.
See QUARTILE.
QUARTILE. Higher and lower quartile are found in 1879 in Donald McAlister, The Law of the Geometric Mean, Proc. R. Soc. XXIX, p. 374: "As these two measures, with the mean, divide the curve of facility into four equal parts, I propose to call them the ’shigher quartile’s and the ’slower quartile’s respectively. It will be seen that they correspond to the ill-named ’sprobable errors’s of the ordinary theory" (OED2). McAlister defined octiles on a similar principle. The topic of McAlister’s paper was suggested by Francis Galton (see LOGNORMAL) and Galton may have had a hand in the terms. However, McAlister’s words seems clear enough.
Upper and lower quartile appear in 1882 in F. Galton, "Report of the Anthropometric Committee," Report of the 51st Meeting of the British Association for the Advancement of Science, 1881, p. 245-260
(From David (1995) and Jeffrey K. Aronson "Francis Galton and the Invention of Terms for Quantiles," Journal of Clinical Epidemiology, 54, (2001) 1191-1194.)
The term QUASI-PERIODIC FUNCTION was introduced by Ernest Esclangon (1876-1954) (DSB, article: Bohl).
QUATERNION (a group of four things) dates to the 14th century in English. The word appears in the King James Bible (Acts 12:4), which refers to "four quaternions of soldiers."
William Rowan Hamilton (1805-1865) used the word to refer to a 4-dimensional object consisting of a real component and three imaginary ones. He introduced quaternions in a paper he presented in 1843, On a new Species of Imaginary Quantities connected with a theory of Quaternions. Hamilton devoted the last 20 years of his life to the development of quaternions; his magnum opus was the Lectures on Quaternions (1853).
See also HAMILTON, VECTOR and VECTOR ANALYSIS. For quaternion terms that have not survived (in their original meaning at least) see TENSOR and VERSOR.
QUEUEING. The OED2 shows a use of "a queueing system" and "a complex queueing problem" in 1951 in David G. Kendall’s "Some Problems in the Theory of Queues," Journal of the Royal Statistical Society, Series B, 13, 151-185 and a use of "queueing theory" in 1954 in Science News. Kendall does not give a history of the "Theory of Queues" but he says that, "the first major study of congestion problems was undertaken by A. K. Erlang in 1908 ... under the auspices of the Copenhagen Telephone Company."
[An interesting fact about the word queueing is that it contains five consecutive vowels, the longest string of vowels in any English word, except for a few obscure words not generally found in dictionaries.]
QUINDECAGON is found in English in 1570 in Henry Billingsley’s translation of Euclid: "In a circle geuen to describe a quindecagon or figure of fiftene angles" (OED2).
The OED2 shows one citation, from 1645, for pendecagon.
QUINTIC was used in English as an adjective in 1853 by Sylvester in Philosophical Magazine: "May, To express the number of distinct Quintic and Sextic invariants."
Quintic was used as a noun in 1856 by Cayley: "In the case of a quantic of the fifth order or quintic" (from his Works, 1889) (OED2).
QUINTILE is found in 1922 in "The Accuracy of the Plating Method of Estimating the Density of Bacterial Populations", Annals of Applied Biology by R. A. Fisher, H. G. Thornton, and W. A. Mackenzie: "Since the 3-plate sets are relatively scanty, we can best test their agreement with theory by dividing the theoretical distribution of 43 values at its quintiles, so that the expectation is the same in each group." There are much earlier uses of this term in astrology [James A. Landau].
QUOTIENT. Joannes de Muris (c. 1350) used numerus quociens.
In the Rollandus Manuscript (1424) quotiens is used (Smith vol. 2, page 131).
Pellos (1492) used quocient.
QUOTIENT (group theory). This term was introduced by Hölder in 1889, according to a paper by Young in 1893.
Quotient appears in English in 1893 in a paper by Cayley, "Note on the so-called quotient G/H in the theory of groups."
QUOTIENT GROUP. Otto Hölder (1859-1937) coined the term factorgruppe. He used the term in 1889.
Quotient group is found in 1893 in Bull. N.Y. Math. Soc. III. 74: "The quotient-group of any two consecutive groups in the series of composition of any group is a simple group" (OED2).
Factor-group appears in English in G. L. Brown, "Note on Hölder’s theorem Concerning the constancy of factor-groups," American M. S. Bull. (1895).
QUOTIENT RING is found in 1946 in Foundations of Algebraic Geometry by Andre Weil: "Furthermore, every quotient-ring derived from this ring and a prime ideal in it will be Noetherian." [Google print search]