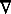Earliest Known Uses of Some of the Words of Mathematics (N)

N-GON is found in 1867-78 in J. Wolstenholme, Math. Probl. (ed. 2): "In the moving circle is described a regular m-gon. .. The same epicycloid may also be generated by the corners of a regular n-gon" [OED].

N-VARIATE is found in J. W. Mauchly, "Significance test for sphericity of a normal n-variate distribution," Ann. Math. Statist. 1 (1940).

See BIVARIATE, MULTIVARIATE, TRIVARIATE and UNIVARIATE.

NABLA (as a name for the Hamiltonian operator 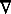, also called DEL). William Robertson Smith (1846-1894) suggested the name to P. G. Tait. Webster’s Third New International Dictionary defines nabla as "an ancient stringed instrument probably like a Hebrew harp of 10 or 12 strings...."

Tait used the symbol 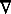for "the very singular operator devised by Hamilton" in An Elementary Treatise on Quaternions (1867, p. 221). Tait made very effective use of the operator in a series of papers, including "On Green’s and other allied theorems" (1870) Scientific Papers I, p. 136. The story of its naming is related in Cargill Gilston Knott’s Life and Scientific Work of Peter Guthrie Tait (1911):

From the resemblance of this inverted delta to an Assyrian harp Robertson Smith suggested the name Nabla. The name was used in playful intercourse between Tait and Clerk Maxwell, who in a letter of uncertain date finished a brief sketch of a particular problem in orthogonal surfaces by the remark "It is neater and perhaps wiser to compose a nablody on this theme which is well suited for this species of composition." [...]

It was probably this reluctance on the part of Maxwell to use the term Nabla in serious writings which prevented Tait from introducing the word earlier than he did. The one published use of the word by Maxwell is in the title to his humorous Tyndallic Ode, which is dedicated to the "Chief Musician upon Nabla," that is, Tait.

In a letter from Maxwell to Tait on Nov. 7, 1870, Maxwell wrote, "What do you call this? Atled?"

In a letter from Maxwell to Tait on Jan. 23, 1871, Maxwell began with, "Still harping on that Nabla?"

Maxwell and Tait were school friends and the background to the fun was Maxwell’s search for a suitable term to use in his own work. In the event Maxwell called the operator 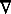the slope: see A Treatise on Electricity and Magnetism (1873, pp.15-16.)  In "On the importance of quaternions in physics" (1890) Scientific Papers II, pp. 303-4 Tait wrote "we must have a name attached to [this remarkable operator] and I shall speak of it as Nabla."

Heaviside also used "nabla" but without enthusiasm, "The fictitious vector 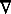... is very important. Physical mathematics is very largely the mathematics of 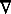. The name Nabla seems, therefore, ludicrously inefficient." ("On the Forces, Stresses, and Fluxes of Energy in the Electromagnetic Field," Philosophical Transactions of the Royal Society of London. A, 183, (1892), p. 431.)

See DEL, VECTOR ANALYSIS and the Earliest Uses of Symbols of Calculus page.

NAPIERIAN LOGARITHM. The term, which honors John Napier, refers to the natural logarithm, although Napier did not strictly use this type of logarithm.

Phil. Trans. (1750) 46, 562 has: "The Logarithms to that Spiral which cuts its Rays at Angles of 45Degrees, are of the Napierian Kind" [Alan Hughes, Associate Editor of the OED].

Napers logarithm is found in 1706 in Synopsis Palmariorum Matheseos: Or, a New Introduction to the Mathematics Containing the Principles of Arithmetic & Geometry Demonstarted, In a Short and Easie Method. [Google print search, James A. Landau]

Napierian appears in Traité élémentaire de calcul différentiel et de calcul intégral (1797-1800) by Lacroix: "Le nombre e se présente souvent dans les recherches analytiques; on le prend pour base d'un système logarithmique, que j'ai appelé Népérien, du nom de Néper, inventeur des logarithmes."

Napierian appears in English in 1816 in a translation of Lacroix’s Differential and Integral Calculus: "A system of logarithms, which we shall call Naperian, from the name of Naper their inventor" [OED].

NAPIER’s CONSTANT or NUMBER is a rarely used name for the number generally denoted by e; see the Earliest Uses of Symbols for Constants. The author of the Encyclopedia of Mathematics entry believes the term has no justification but the MacTutor entry on John Napier supplies a hint of one.

Surprisingly a JSTOR search found only one use of Napier’s constant, viz. in Steven F. Maier, David W. Peterson, James H. Vander Weide, “A Monte Carlo Investigation of Characteristics of Optimal Geometric Mean Portfolios,” The Journal of Financial and Quantitative Analysis, 12, No. 2, June 1977. The term Napier’s constant was used twice in an episode of the television series The X-Files titled “Paper Clip,” which originally aired on Sept. 29, 1995.

NASH EQUILIBRIUM, a solution concept in non-cooperative game theory, was introduced by John Nash in his PhD dissertation and published in two papers, "Equilibrium Points in n-Person Games," Proceedings of the National Academy of Sciences of the United States of America, 36, (1950), 48-49 and "Non-Cooperative Games," Annals of Mathematics, 54, (1951), 286-295. The concept is generally referred to by his name, see e.g. I. L. Glicksberg "A Further Generalization of the Kakutani Fixed Point Theorem, with Application to Nash Equilibrium Points," Proceedings of the American Mathematical Society, 3, (1952), 170-174.  Nash received the 1994 Nobel Prize in Economic Science for this contribution to game theory.

See THEORY OF GAMES.

NATURAL LOGARITHM (early sense). According ti the DSB, Thomas Fantet de Lagny (1660-1734) "attempted to establish trigonometric tables through the use of transcription into binary arithmetic, which he termed 'natural logarithm' and the properties of which he discovered independently of Leibniz."

NATURAL LOGARITHM (modern sense). Boyer (page 430) implies that Pietro Mengoli (1625-1686) coined the term: “Mercator took over from Mengoli the name ‘natural logarithm’ for values that are derived by means of this series.”

Joseph Ehrenfried Hofmann, in Classical Mathematics: A Concise History of Mathematics in the Seventeenth and Eighteenth Centuries (1959), writes, “Mercator, himself, took over Mengoli’s designation of ‘natural logarithms’ ... ”

Natural logarithm is found (in Latin) in 1659 in Mengoli’s Geometriae speciosae Elementa. [Siegmund Probst]

Siegmund Probst writes that the term logarithmus naturalis apparently does not appear in Mercator’s Logarithmo-technia sive methodus construendi logarithmos nova, accurata, & facilis in 1668.

Mercator does use the term natural logarithm (in Latin) in 1668 in Some Illustration Of the Logarithmotechnia, in Philosophical Transactions, volume 3, No. 38, August 17/27 1668, 759-764. [Siegmund Probst]

Merriam-Webster dates the term in English to 1746.

In 1748 Euler called these logarithms “natural or hyperbolic” in his Introductio, according to Dunham (page 26), who provides a reference to Vol. I, page 97, of the Introductio.

NATURAL NUMBER. Chuquet (1484) used the term progression naturelle for the sequence 1, 2, 3, 4, etc.

In 1727, Bernard le Bouyer de Fontenelle (1657-1757) wrote in Elemens de la Geometrie de l'infini: "Pour mieux concevoir l'Infini, je considere la suite naturelle des nombres, dont l'origine est 0 ou 1" [Gunnar Berg].

Natural number appears in 1763 in The method of increments by William Emerson: "To find the product of all natural numbers from 1 to 100" [OED].

Natural number, defined as the numbers 1, 2, 3, 4, 5, etc., appears in the 1771 Encyclopaedia Britannica in the Logarithm article.

In 1889, Elements of Algebra by G. A. Wentworth has: "The natural series of numbers begins with 0; each succeeding number is obtained by adding one to the preceding number, and the series is infinite."

Apparently, except for the various Random House dictionaries, all modern dictionaries define the term natural number to exclude 0. [The term whole number is defined to include 0.]

Gerald A. Edgar wrote in sci.math that he has found that algebra texts tend to include 0 and analysis texts tend to exclude it.

Bertrand Russell in his 1919 Introduction to Mathematical Philosophy writes:

To the average educated person of the present day, the obvious starting-point of mathematics would be the series of whole numbers,

1, 2, 3, 4, . . . etc.

Probably only a person with some mathematical knowledge would think of beginning with 0 instead of with 1, but we will presume this degree of knowledge; we will take as our starting-point the series:

0, 1, 2, 3, . . . n, n + 1, . . .

and it is this series that we shall mean when we speak of the "series of natural numbers."

John Conway writes:

The older nomenclature was that "natural number" meant "positive integer." This was unfortunate, because the set of non-negative integers is really much more "natural" in the sense that it has simpler properties. So starting in about the 1960s lots of people (including me) started to use "natural number" in the inclusive sense. After all, for the positive integers we have the much better term "positive integer."

Some authors use "natural numbers" as a synonym for "positive integers" 1, 2, 3, ..., obliging one to use the more cumbersome name "nonnegative integers" for 0, 1, 2, .... Besides, in this age, we should accept 0 on the same footing with 1, 2, 3, ... .

NAUGHT or NOUGHT. See ZERO.

NEGATIVE. According to Burton (page 245), Brahmagupta introduced negative numbers and a word equivalent to negative.

In his Ars Magna (1545) Cardano referred to negative numbers as numeri ficti. In speaking of the roots of an equation, he wrote, "una semper est rei uera aestimatio, altera ei aequalis, ficta" (Smith vol. 2, page 260).

Stifel (1544) called negative numbers numeri absurdi. He spoke of zero as "quod mediat inter numeros veros et numeros absurdos" (Smith vol. 2, page 260).

The word negative was used by Scheubel (1551) (Smith vol. 2, page 260).

Robert Recorde in Whetstone of Witt (1557) used absurde nomber: "8 - 12 is an Absurde nomber. For it betokeneth lesse then nought by 4" [OED].

Napier (c. 1600) used the adjective defectivi to designate negative numbers (Smith vol. 2, page 260).

Negative was used in English in 1673 by John Kersey in Elements of Algebra: "A negative Root (which Cartesius calls a false Root) expresseth a Quantity whose Denomination is opposite to an affirmative, as -5 or -20" [OED].

NEGATIVE BINOMIAL DISTRIBUTION appears in Major Greenwood and G. Udny Yule’s "An Inquiry into the Nature of Frequency Distributions Representative of Multiple Happenings with Particular Reference to the Occurrence of Multiple Attacks of Disease or of Repeated Accidents," Journal of the Royal Statistical Society, Vol. 83, No. 2. (Mar., 1920), pp. 255-279. [David (1995)].

NEIGHBORHOOD OF A POINT. In an 1877 paper in the Messenger of Mathematics, Arthur Cayley wrote, "The lines in the neighbourhood of a point of maximum, or of minimum, parameter are ovals surrounding the point in question, each oval being itself surrounded by the consecutive oval" [University of Michigan Historical Math Collection].

Neighborhood of a point appears in 1891 in George L. Cathcart’s translation of An Introduction to the Study of the Elements of the Differential and Integral Calculus by Axel Harnack:

With the foregoing considerations we have attained the conception of the Region or Neighbourhood of a point. By it we mean an arbitrarily small but still always finite interval at both sides of the value x.

The epicycloid with two cusps (the dotted curve of fig. 39, which, from its shape, we may call the nephroid) presents also many interesting relations.

The term NET was coined by J. Kelley. He had considered using the term "way" so the analog of subsequence would be "subway." E. J. McShane also proposed the term "stream" since he thought it was intuitive to think of the relation of the directed set as "being downstream from" (McShane, Partial Orderings and Moore-Smith Limits, 1950, p. 282).

NEW MATH. New mathematics is found in Time magazine of Feb. 3, 1958, in the heading, "The new mathematics" [OED].

New math is found in an article which appeared in numerous newspapers on Sept. 25, 1960: “But the ‘new math’ is being promoted energetically by such influential bodies as the U. S. Office of Education, the National Science Foundation, the National Education Association, the Mathematical Association of America, the College Entrance Examination Board and the Carnegie Corporation.”

NEWTON’S METHOD and the NEWTON-RAPHSON METHOD. By 1669 Isaac Newton had devised a method for approximating the roots of equations. The method circulated among his friends and is first referred to in print in the Algebra (1685) of John Wallis: “Another Method of Approximation, by Mr. Isaac Newton.” In 1695 Wallis used the phrase “Mr. Newton’s Method of Approximation for the Extracting of Roots” in “A Discourse concerning the Methods of Approximation in the Extraction of Surd Roots,” Phil. Trans. 19, p. 2. (The quotations are from the OED).

In 1695 Wallis also referred to a modification of Newton’s method given by Joseph Raphson in his Analysis aequationum universalis (1690). This eventually became the preferred method: Lagrange described it as “plus simple que celle de Newton.” However Raphson’s modification came to be called “Newton’s method.” The origins of the methods were examined by the historian Florian Cajori, most thoroughly in his “Historical note on the Newton-Raphson method of approximation,” American Mathematical Monthly, 18, (1911), 29-32. Cajori (p. 31) concluded that “the ‘Newton-Raphson method’ would be a designation more nearly representing the facts of history than is ‘Newton’s method.’” Cajori’s term is now widely used although the older term, “Newton’s method,” survives.

NEXT TO CONVEX. In a post to the geometry forum, Michael E. Gage wrote that he believed the term was coined by Gromov in "Hyberbolic manifolds, groups and actions," Annals of Mathematics Studies, v. 97, page 183.

NEYMAN ALLOCATION. This method for allocating sample numbers to different strata was proposed by Jerzy Neyman, "On the two different aspects of the representative method; the method of stratified sampling and the method of purposive selection," J. R. Statist. Soc., 97, (1934), 558-625. The term "Neyman allocation" seems to have come into use in the 1950s. See e.g. W. Edwards Deming Journal of the American Statistical Association, 51, (1956), p. 31. (JSTOR search.) The method was proposed earlier by Aleksandr Aleksandrovich Chuprov (1874-1926) in "On the mathematical expectation of the moments of frequency distributions in the case of correlated observations," Metron, 2, (1923), 461-493, 646-683.

See STRATIFIED SAMPLING.

NEYMAN-PEARSON (FUNDAMENTAL) LEMMA. When J. Neyman and E. S. Pearson first described the construction of a best critical region they did not dignify the inequality they obtained with a title (Section III of "On the Problem of the Most Efficient Tests of Statistical Hypotheses," Philosophical Transactions of the Royal Society of London, Ser. A (1933), 231, 289-337.) The custom of calling it a "lemma" seems to have been established by Neyman; see his "Tests of Statistical Hypotheses Which are Unbiased in the Limit," Annals of Mathematical Statistics, 9, (1938), 69-86. The phrase "Neyman-Pearson lemma" appears in P. L. Hsu "On the Power Functions of the E²-Test and the T²-Test," Annals of Mathematical Statistics, 16, (1945), pp. 278-286 and the "Neyman-Pearson fundamental lemma" in E. L. Lehmann’s "On Optimum Tests of Composite Hypotheses with One Constraint," Annals of Mathematical Statistics, 18, (1947), p. 487 [John Aldrich].

See the entry on Hypothesis and hypothesis testing.

NILPOTENT. See idempotent.

The term NINE-POINT CIRCLE first appears in 1820 in "Recherches sur la détermination d'une hyperbola équilatére, au moyen de quatres conditions données" by Charles-Julien Brianchon (1783-1864) and Poncelet (DSB).

Nine-points circle appears in English in 1865 in Brande & Cox, Dict. Sci., etc., which has: "The circle which passes through the middle points of the sides of a triangle is referred to by Continental writers as 'the nine-points circle' [OED].

Nine-point circle appears in W. F. Mc Michael, "Elementary proof of the contact of the nine-point circle with the inscribed and escribed circles," Mess. (1881).

Nine-point circle also appears in English in C. Pendlebury, "Proof of a nine-point circle theorem," Ed. Times (1881).

In Plane Geometry (1904), James Sturgeon Mackay wrote, "The designation often given to the circle, namely, Euler’s circle, is quite erroneous" [Ken Pledger].

According to Eves (page 437), the circle is sometimes called Euler’s circle because of misplaced credit, and in Germany the circle is called Feuerbach’s circle.

NODE. In 1753 Daniel Bernoulli used the Latin word noeud [James A. Landau].

NOETHERIAN RING (named for Emmy Noether) is defined in Claude Chevalley “On the Theory of Local Rings,” Annals of Mathematics, 44, (1943), 690-708. (JSTOR search)

NOETHER’S THEOREM (named for Max Noether). Noether’s fundamental theorem is found in English in H. J. Baker, "On Noether’s fundamental theorem," Math. Ann. (1893).

Noether’s theorem is found in English in F. S. Macaulay, "The theorem of residuation, Noether’s theorem, and the Riemann-Roch theorem," Lond. M. S. Proc. (1899).

NOME. The OED2 indicates this word comes to English from the French nôme, the second element in binôme (binomial).

In 1665 Collins used the term in English in correspondence: "The limits of such equations as have but two nomes."

In 1704 Harris’s Lexicon technicum has: "Nome, in Algebra, is any Quantity with a Sign prefixed to it, and by which 'tis usually connected with some other Quantity, and then the whole is called a Binomial, a Trinomial, &c."

About 1727 nome appears in English meaning "one of the 36 territorial divisions of ancient Egypt." Most recent dictionaries indicate the word is derived from the Greek nomos meaning "a pasture or district"; however, the OED2 indicates the word is derived a Greek word meaning "to divide."

According to a post by Eric Conrad to the history of mathematics mailing list, "the term nome for the argument q in elliptic function theory comes from a Greek word meaning to partition or divide. Many identities in elliptic function theory have combinatorial interpretations involving partitions. For example, the Fourier expansion of the elliptic function dn leads to an identity which counts partitions of an integer into a sum of four squares."

The term NOMOGRAPHY is due to Philbert Maurice d'Ocagne (1862-1938). It occurs in his Traité de nomographie (1899) (DSB).

NONAGON is dated 1639 in MWCD10.

In 1688, R. Holme, Armoury has: "An Henneagon, or Enneagon or Nonagon, a fort of nyne corners" [OED].

The 1828 Webster dictionary defines nonagon and enneagon.

NON-CANTORIAN appears in Paul J. Cohen and Reuben Hersh, "Non-Cantorian Set Theory," Scientific American, December 1967.

The term also appears in 1967 in the article "Set Theory" in The Encyclopedia of Philosophy [James A. Landau].

The term NON-EUCLIDEAN GEOMETRY was introduced by Carl Friedrich Gauss (1777-1855) (Sommerville). Gauss had earlier used the terms anti-Euclidean geometry and astral geometry (Kline, page 872).

Non-Euclidean geometry is found in 1868 in the title of the paper "Saggio di interpretazione della geometria non-euclidea" by Eugenio Beltrami.

Non-Euclidean geometry is found in English in 1872 in A. Cayley "On the Non-Euclidian Geometry", Mathematische Ann. vol. 5. p. 630: "The theory of Non-Euclidean Geometry as developed in Dr. Klein’s paper 'Uber die Nicht-Euclidische Geometrie' may be illustrated by showing how in such a system we actually measure a distance and an angle" [David B. Shirt, Senior Science Editor, OED].

NONINFORMATIVE (or UNINFORMATIVE) PRIOR. These terms entered circulation in the 1960s. A JSTOR search found an earliest appearance of noninformative in G. E. P. Box & George C. Tiao "A Bayesian Approach to the Importance of Assumptions Applied to the Comparison of Variances," Biometrika, 51, (1964), 153-167. Box and Tiao were referring to Jeffreys’s invariant prior.

See JEFFREYS PRIOR.

NON-NORMAL appears in 1929 in Biometrika in the heading: "On the distribution of the ratio of mean to standard deviation in small samples from non-normal universes" [OED].

NONPARAMETRIC (referring to a statistical inference) is found in 1942 in Jacob Wolfowitz (1910-1981), "Additive Partition Functions and a Class of Statistical Hypotheses," Annals of Mathematical Statistics, 13, 247-279  "We shall refer to this situation [where the knowledge of the parameters, finite in number, would completely determine the distributions involved] as the parametric case, and denote the opposite case, where the functional forms of the distributions are unknown, as the non-parametric case." p. 264. (OED, David, 1995)

NON-STANDARD ANALYSIS was introduced by Abraham Robinson in a 1961 paper "Non-standard Analysis," Proceedings of the Royal Academy of Sciences of Amsterdam Series A, 64, 432-440. "It is our main purpose to show that these [non-standard models of the real number system] provide a natural approach to the age old problem of producing a calculus involving infinitesimal (infinitely small) and infinitely large quantities. As is well known, the use of infinitesimals, strongly advocated by Leibnitz and unhesitatingly accepted by Euler fell into disrepute after the advent of Cauchy’s methods which put Mathematical Analysis on a firm foundation." (p. 433)

NON-TERMINATING DECIMAL. Interminate decimal is found in 1714 in S. Cunn, Treat. Fractions Pref.: "The Reverend Mr. Brown, in his System of Decimal arithmetick, manages such interminate Decimals as have a single Digit continually repeated" [OED].

Non-terminating decimal is found in 1903 in A College Algebra by G. A. Wentworth: "In the decimal scale of notation a common fraction in its lowest terms will produce a non-terminating decimal if its denominator contains any prime factor except 2 and 5." [Google print search]

NORM and NORMAL. According to the OED, in Latin norma could mean a square used by carpenters, masons, etc., for obtaining right angles, a right angle or a standard or pattern of practice or behaviour. These meanings are reflected in the mathematical terms based on norm and normal.

NORM has at least three current meanings. The first two, from algebra and analysis, may apply to the same things, which can be confusing.

Norm in number theory (and then algebra) comes from the term norma introduced by Carl Friedrich Gauss (1777-1855) in 1832 in "Theoria residuorum biquadraticorum, Commentatio secunda" Commentationes Recentiones Soc. R. Scient. Gottingensis VII. Class. math. 98 Werke II, p. 132. Gauss was considering the complex integer (GAUSSIAN INTEGER) a + ib and its norma referred to a² + b².

In 1856 W. R. Hamilton used norm to refer to a² + b² for any complex number a + ib. The OED quotes from his Notebook in H. Halberstam & R. E. Ingram Math. Papers Sir W. R. Hamilton (1967) III. 657, "a + ib is said to be a complex number, when a and b are integers, and i = 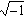; its norm is a² + b²; and therefore the norm of a product is equal to the product of the norms of its factors."

In 1911-12 M. Bôcher & L. Brand used norm to refer to | a₁ |² + ... +| a_k |² for the "complex quantity" (a₁, ... a_k) in "On Linear Equations with an Infinite Number of Variables," Annals of Mathematics, 2nd Ser., 13, p. 168.

In 1967 S. MacLane & G. Birkhoff Algebra v. 187, "Each quadratic field Q(√ d), with the elements σ = r + s√d, has as automorphisms the identity and σ → 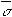 = r - s√d. The product σ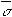 = r² + s²d is called the norm N(σ) of σ." (OED).

Norm in analysis is identified with distance and a norm is required to satisfy the triangle inequality, which Gauss’s norma does not. 

In 1921 Albert A. Bennett "Normalized Geometric Systems," Proc. National Acad. Sci. U.S.A. 7 p. 84: "The notion of norm or numerical value of a complex quantity, c = a + b√- 1, namely, |c| = √(a² + b²), as it arises in algebra, has a more or less immediate generalization to more extensive matric systems." (OED)

In 1922 S. Banach defined “la norme” for an abstract linear space in “Sur les opérations dans les ensembles abstraits et leur application aux équations integrales”, Fundamenta Mathematicae, 3, pp. 135-6. Among the examples (pp. 167-8) is ║φ║ defined by

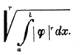
The norm of a matrix. In his Theory of Matrices in Numerical Analysis (1964, p. 55) A. S. Householder writes, "The notion of norms is fundamental in functional analysis, but until recently does not often appear in the literature of numerical analysis or of the theory of matrices." Things changed around 1940. For example, the term "norm" appears in Harold Hotelling "Some New Methods in Matrix Calculation," Annals of Mathematical Statistics, 14, (1943), p. 11 and there is a general discussion of norms in Albert H. Bowker "On the Norm of a Matrix," Annals of Mathematical Statistics, 18, (1947), 285-288. The norm used by Hotelling is the "absolute value of a matrix" described in 8.09 (p. 125) of J. H. M. Wedderburn’s Lectures on Matrices (1934).  Wedderburn traces the idea back to Peano in 1887.

Another usage, unrelated to those given, is the norm of a partition of an interval used e.g. in Riemann integration, to indicate the fineness of the sub-division. The term is found in "On the Integration of Discontinuous Functions" by Henry John Stephen Smith, which was read before the London Mathematical Society on June 10, 1875: "We may term d the norm of the division; it is evident that there is an infinite number of different divisions having a given norm; and that a division appertaining to any given norm, appertains also to every greater norm." [Google print search]

[The above was contributed by John Aldrich.]

Norm of a vector. On page 57 of his 1908 paper “Über die Auflösung linearer Gleichungen mit unendlich vielen Unbekannten,” Rendiconti del Circolo Matematico di Palermo, 25 (1908), Erhard Schmidt defines for a function A(x), x = 1, 2, 3 ..., which, he says in a footnote, can be regarded as a vector in an infinite-dimensional space, a positive quantity ||A||, the Euclidean norm, which he calls the length, and calls a vector “normirt,” if its length is equal to 1. [Jan Peter Schäfermeyer]

The NORMAL distribution has been studied under various names for nearly 300 years. Some names were derived from ERROR, e.g. the law of error, the law of facility of errors and the law of frequency of errors. Some were derived from persons associated with the distribution, e.g. Laplace’s second law and the GAUSSIAN law. Stigler remarks in his "Stigler’s law of eponymy" (see EPONYMY) that as the distribution has never been called after Abraham De Moivre, who worked on it in 1733, we may conclude that he was its originator. (See also Symbols Associated with the Normal Distribution on the Symbols in Probability and Statistics page.)

According to Kruskal & Stigler, the term normal was used, apparently independently, by Charles S. Peirce (1873) in an appendix to a report of the US Coast Survey (reprinted in Stigler (1980, vol. 2), Wilhelm Lexis Theorie der Massenerscheinungen in der menschlichen Gesellschaft (1877) and Francis Galton 'Typical laws of heredity' (1877).

Of the three, Galton had most influence on the development of Statistics in Britain and, through his ‘descendants’ Karl Pearson and R. A. Fisher, on Statistics worldwide. In the 1877 article Galton used the phrase "deviated normally" only once (p. 513)--his name for the distribution was "the law of deviation." However in the 1880s he began using the term "normal" systematically: chapter 5 of his Natural Inheritance (1889) is entitled "Normal Variability" and Galton refers to the "normal curve of distributions" or simply the "normal curve." Galton does not explain why he uses the term "normal" but the sense of conforming to a norm ( = "A standard, model, pattern, type." (OED)) seems implied.

Karl Pearson wrote, in his "Contributions to the Mathematical Theory of Evolution," Philosophical Transactions of the Royal Society of London. A, 185, (1894) p. 72, "A frequency-curve, which for practical purposes, can be represented by the error curve, will for the remainder of this paper be termed a normal curve." Later Pearson seemed to imply that he had introduced the term: "Many years ago I called the Laplace-Gaussian curve the normal curve ..." (Biometrika, 13, (1920), p. 25). While Pearson did not introduce the term, it is fair to say that his "consistent and exclusive use of this term in his epoch-making publications led to its adoption throughout the statistical community." (DSB) Curiously a main theme in Pearson’s scientific work was that data did not ‘normally’ follow this distribution and that alternative distributions had to be devised. (See the entry on Pearson curves.)

Once the basic normal terminology was adopted NORMAL appeared in many expressions. These must have seemed more or less obvious to their creators and were probably re-invented many times.

Normal correlation appears in W. F. Sheppard, "On the application of the theory of error to cases of normal distribution and normal correlation," Phil. Trans. A, 192, (1899) page 101, and Proc. Roy. Soc. 62, page 170 (1898) [James A. Landau].

Normal curve appears in Galton’s Natural Inheritance (1889)--see above.

Normal distribution appears in Karl Pearson’s 1897 "Contributions to the Mathematical Theory of Evolution. II. Skew Variation in Homogeneous Material," Philosophical Transactions of the Royal Society of London. A, 186, (1895), pp. 343-414: "A random selection from a normal distribution" [OED].

Normal deviate is found in 1925 in R. A. Fisher, Statistical Methods for Research Workers p. 47:  "Table I. shows that the normal deviate falls outside the range +/-1.598193 in 10 per cent of cases" [OED].

Normal law is found in Francis Galton’s "Results Derived from the Natality Table of Korosi by Employing the Method of Contours or Isogens," Proceedings of the Royal Society, 55, (1894), p. 23 (JSTOR search).

Normal population appears in Karl Pearson’s "Contributions to the Mathematical Theory of Evolution," Philosophical Transactions of the Royal Society of London. A, 185. (1894), p. 104. [JSTOR search].

Normal sample is found in R. A. Fisher’s The Goodness of Fit of Regression Formulae and the Distribution of Regression Coefficients. Journal of the Royal Statistical Society, 85, No. 4. (1922), p. 599 [JSTOR search]

Normal universe is found in W. A. Shewhart & F. W. Winters "Small Samples--New Experimental Results" Journal of the American Statistical Association, 23, (Jun., 1928), p. 145. [JSTOR search].

Normal variate was in wide use in the 1930s and is found in Joseph Pepper’s "Studies in the Theory of Sampling," Biometrika, 21, (1929), p. 239. [JSTOR search]

Normality appears in Karl Pearson "Contributions to the Mathematical Theory of Evolution. II. Skew Variation in Homogeneous Material," Philosophical Transactions of the Royal Society of London. A, 186, (1895), p. 386. [JSTOR search]

This entry was contributed by John Aldrich drawing on Kruskal & Stigler "Normative Terminology" in Stigler (1999), Hald (1998, p. 356) and Walker (p. 185). See CENTRAL LIMIT THEOREM, ERROR and GAUSSIAN.

The term NORMAL EQUATION in least squares was introduced by Gauss in 1822 [James A. Landau]. Kruskal & Stigler‘s "Normative Terminology" (in Stigler (1999)) consider various hypotheses about where the term came from but do not find any very satisfactory.

NORMAL MATRIX. C. C. MacDuffee, The Theory of Matrices, Springer (1933, p. 76) refers to O. Toeplitz, "Das algebraische Analogon zu einem Satze von Fejér," Mathematische Zeitschrift, 2, (1918), 187-197.

NORMAL NUMBER. The concept of a normal number was introduced by Émile Borel in "Les probabilités dénombrables et leurs applications arithmétiques," Rend. Circ. Mat. Palermo, 27 (1909), 247-271, reprinted in Oeuvres T. II. Borel’s result that almost all numbers in [0,1] are normal was important in both number theory and probability theory. For the former aspect see the Encyclopedia of Mathematics entry Normal number and, for the latter, Section 3.3 of Vovk & Shafer "The Origins and Legacy of Kolmogorov’s Grundbegriffe," Statistical Science (2006) Number 1 70-98. Borel’s result was the earliest version of the strong law of large numbers.

See LAW OF LARGE NUMBERS.

NORMAL SPACE in topology. Normale Räume are defined in P Alexandroff and P. Urysohn “Zur Théorie der topologischen Räume,” Mathematische Annalen, 92, (1924), 258-266. In their Topologie Alexandroff and Hopf (1935, p. 68) also call them T₄ spaces. A JSTOR search found the English phrase in M. H. Stone’s “Boolean Algebras and their Application to Topology,” Proceedings of the National Academy of Sciences 20, (1934), 197-202. See the Encyclopedia of Mathematics entry.

See the entry T₁ SPACE.

NORMAL SUBGROUP. According to Kramer (p. 388), Galois used the adjective "invariant" referring to a normal subgroup.

According to The Genesis of the Abstract Group Concept (1984) by Hans Wussing, "The German Normalteiler (normal subgroup) goes back to Weber [H., Lehrbuch der Algebra, vol. 1, Braunschweig, 1895. p.511] and is possibly linked to Dedekind’s term Teiler (divisor), which was employed in ideal theory" [Dirk Schlimm].

Normal subgroup is found in English in 1908 in An Introduction to the Theory of Groups of Finite Order by Harold Hilton: "Similarly, if every element of G transforms a subgroup H into itself, H is called a normal, self-conjugate, or invariant subgroup of G (or 'a subgroup normal in G')."

G. A. Miller writes in Historical Introduction to Mathematical Literature (1916), "In the newer subjects the tendency is especially strong to use different terms for the same concept. For instance, in the theory of groups the following seven terms have been used by various writers to denote a single concept: invariant subgroup, self-conjugate subgroup, normal divisor, monotypic subgroup, proper divisor, distinguished subgroup, autojug."

NORMALCY, meaning normality, is found in 1857 in Mathematical Dictionary and Cyclopedia of Mathematical Science by Charles Davies and William Guy Peck. The word was used more famously by President W. G. Harding in 1920, in a non-mathematical sense.

NORMALIZER appears in German as Normalisator in Theorie der Gruppen von endlicher Ordnung, 2nd ed., by A. Speiser [Huw Davies].

NTH is found in 1756 in Philosophical transactions of the Royal Society of London 49/84: “If the given series..be raised to the n^th power, the terms of the series will truly exhibit all the different chances in all the proposed (n) observations.” [OED]

Nth is found in 1820 in Functional Equations by Babbage: "To find periodic functions of the nth order...."

Nth is found in 1831 in Elements of the Integral Calculus (1839) by J. R. Young:

In all the foregoing examples, the first differential coefficient is given to determine the primitive function from which it has been derived; when, however, it is not the first, but the nth differential coefficient which is given, then by a first integration, we shall arrive at the preceding or n - 1th differential coefficient; by a second integration we get the n - 2th coefficient; and, by thus continuing the integration, we at length arrive at the original function.

[John Aldrich, based on David (2001)]

NULL CLASS is found in Bertrand Russell’s Principles of Mathematics (1903). G. Peano’s "Dizionario di Matematica," Revue de mathématiques, 7, (1900-1), 160-172 has an entry under Nulla: "La classe nulle, classe non contenente individui ..."

See NULL SET and EMPTY SET.

NULL HYPOTHESIS. See HYPOTHESIS and HYPOTHESIS TESTING.

NULLITY appears in 1884 in James Joseph Sylvester, "Lectures on the Principles of Universal Algebra," Amer. Jrnl. Math. VI. (1883-4) 274 Coll Math Papers p. 211:

The absolute zero for matrices of any order is the matrix all of whose elements are zero. It possesses so far as regards multiplication .. the distinguishing property of the zero, viz. that when entering into composition with any other matrix .. the product .. is itself over again... This is the highest degree of nullity which any matrix can possess, and (regarded as an integer) will be called ω, the order of the matrix... In general.., if all the minors of order ω - i + 1 vanish, but the minors of order ω - i do not all vanish, the nullity will be said to be i.

NULL SPACE appears in 1884 in Arthur Buccheim’s "Proof of Professor Sylvester’s ‘Third law of motion,’" Philosophical Magazine, 18, 459-460.  This "law of motion" for matrices states that "the nullity of the product of two matrices is not less than the greater of their nullities, but not greater than the sum of the two nullities." 

Buccheim writes,  "A linear space of (α-1) dimensions will be called an α-point... A matrix A of order n is considered as operating on the coordinates of the points of an n-point... If A is of nullity α, the equation A(x₁...x_n) = 0 is satisfied by all the points of a certain α-point, and conversely. I call this α-point the null space of A." (OED).

The word NUMBER entered English around 1300. The OED gives several quotations and traces the word to the Anglo-Norman and to the Old French, and ultimately to the Latin numerus.

NUMBER LINE. An earlier term was scale of numbers.

Number line seems to appear in the June 1899 Telephone Magazine: “Gauss’s representation of complex numbers is not systematic, on account of the direct step from the number line to the num-...” This use is found using Google books search, which only provides snippet views of this periodical; thus the word “seems.” [James A. Landau]

Number Line appears several times in Herbert Ellsworth Slaught, "The evolution of numbers — An historical drama in two acts," American Mathematical Monthly 35 #3 (March 1928), 146-154. [Dave L. Renfro, Pat Ballew]

Lawrence M. Henderson, "An Alternative Technique for Teaching Subtraction of Signed Numbers," The Mathematics Teacher, Nov. 1945 has: "In teaching subtraction of signed numbers, I first draw a number scale."

Number line is found in January 1956 in "An exploratory approach to solving equations" by Max Beberman and Bruce E. Meserve in The Mathematics Teacher: "In an earlier paper we described a procedure by which students could ’solve' equations and inequalities using a number line. The set of points on a number line is in one-to-one correspondence with the set of real numbers."

NUMBER THEORY. According to Diogenes Laertius, Xenocrates of Chalcedon wrote a book titled The theory of numbers. However, the most famous classical work on number theory was the Arithmetika of Diophantus. See the entry ARITHMETIC.

A letter written by Blaise Pascal to Fermat dated July 29, 1654, includes the sentence, "The Chevalier de Mèré said to me that he found a falsehood in the theory of numbers for the following reason."

The term appears in 1798 in the title Essai sur la théorie des nombres by Adrien-Marie Legendre (1752-1833).

Zahlentheorie appears in 1802 in Geschichte der griechischen Astronomie bis auf Eratosthenes by Johann Konrad Schaubach.

In English, theory of numbers appears in 1811 in the title An elementary investigation of the theory of numbers by Peter Barlow.

Number theory appears in 1853 in Manual of Greek literature from the earliest authentic periods to the close of the Byzantine era by Charles Anthon: "The ethics of the Pythagoreans consisted more in ascetic practice and in maxims for the restraint of the passions, especially of anger, and the cultivation of the power of endurance, than in scientific theory. What of the latter they had was, as might be expected, intimately connected with their number-theory" [University of Michigan Digital Library].

Number theory appears in 1864 in A history of philosophy in epitome by Dr. Albert Schwegler, translated from the original German by Julius H. Seelye: "Not only the old Pythagoreans, who have spoken of him, delighted in the mysterious and esoteric, but even his new-Platonistic biographers, Porphyry and Jamblichus, have treated his life as a historico-philosophical romance. We have the same uncertainty in reference to his doctrines, i. e. in reference to his share in the number-theory. Aristotle, e. g. does not ascribe this to Pythagoras himself, but only to the Pythagoreans generally, i. e. to their school" [University of Michigan Digital Library].

Number theory appears in 1912 in the Bulletin of the American Mathematical Society [OED].

The words NUMERATOR and DENOMINATOR are found in 1202 in Liber abbaci by Leonardo of Pisa:

Cum super quemlibet numerum quedam uirgula protracta fuerit, et super ipsam quilibet alius numerus descriptus fuerit, superior numerus partem uel partes inferioris numeri affirmat; nam inferior denominatus, et superior denominans appellatur. Vt si super binarium protracta fuerit uirgula, et super ipsam unitas descripta sit ipsa unitas unam partem de duabus partibus unius integri affirmat, hoc est medietatem sic 1/2 [When above any number a line is drawn, and above that is written any other number, the superior number stands for the part or parts of the inferior number; the inferior is called the denominator, the superior the numerator. Thus, if above the two a line is drawn, and above that unity is written, this unity stands for one part of two parts of an integer, i. e., for a half, thus 1/2].

NUMERICAL ANALYSIS. Although the name numerical analysis is fairly new, the concerns of the subject go back centuries. Thus H. H. Goldstine’s A History of Numerical Analysis from the 16^th through the 19^th Century (1977) begins with the invention of LOGARITHMS.

Numerical analysis is found in 1730 in The Present State of the Republick of Letters. For March 1730. This is a review of Mathematique Universelle by P. Castell: “The numerical Analysis (or the small Analysis, as ’tis sometimes term’d) composes the second part of this Algebra, and is perhaps a treatise of as great variety, and made here as amusing and entertaining to read, as Algebra has been generally deem’d dry and difficult. The Author has added to it several curious arts, that depend upon Algebra. And first we find the analysis of Numbers, their generation, their properties, their magick, and all the other pretended mysteries.” [Google print search, James A. Landau]

Lagrange wrote a paper “Essai d'analyse numérique sur la transformation des fractions,” which appeared in 1799 in Journal De l’ecole Polytechnique, Vol. II. An English translation of this paper appeared in Thomas Leybourn, ed The Mathematical Repository, New Series Volume I (1806) under the title “An Essay of Numerical Analysis, on the Transformation of Fractions.”

The phrase numerical analysis was used intermittently in the 19^th century but it only became the generally accepted name for the subject some decades into the 20^th century.

Numerical analysis appears in 1853 in A dictionary of science, literature & art in a discussion of the rule of false position: "The rules given for the solution of questions in double position, are founded on certain principles of algebra, which may be applied with much greater facility to the immediate solution of the questions themselves. Such questions, therefore, cannot be considered as properly belong to arithmetic, but to what may be denominated numerical analysis" [University of Michigan Digital Library].

It appears in S. Réalis, "Questions d'analyse numérique," N. C. M. V. (1879).

In German the term numerisches Rechnen became standard: see e.g. the 1902 article by R. Mehmke in the Encyklopädie Band I Teil II p. 941 and the 1924 book Vorlesungen über numerisches Rechnen by C. Runge and H. König. Meanwhile in English there was still no standard term. E. T. Whittaker & G. Robinson’s well-known book of 1924 is called The Calculus of Observations: A Treatise on Numerical Mathematics.

Numerical mathematical analysis occurs in 1930 in the title Numerical Mathematical Analysis by J. B. Scarborough. "The object of this book is to set forth in a systematic manner ... the most important principles, methods and processes used for obtaining numerical results; and also methods and means for estimating the accuracy of such results." (Preface) (OED)

The form numerical analysis re-appears in the 1940s. See Randolph Church, "Numerical analysis of certain free distributive structures," Duke Math. J. 6 (1940) and from 1946 Ann. Computation Lab. Harvard Univ. 1 338 (heading) Bibliography of numerical analysis. (OED)

In the 1950s the term became established with the authors of textbooks/treatises, e.g. from 1952, D. R. Hartree Numerical Analysis. (OED)

[John Aldrich, James A. Landau]

NUMERICAL DIFFERENTIATION is found in W. G. Bickley, "Formulae for Numerical Differentiation," Math. Gaz. 25 (1941) [James A. Landau].

NUMERICAL INTEGRATION. See the entry QUADRATURE.