Earliest Known Uses of Some of the Words of Mathematics (T)
Last revision: Apr. 13, 2019
T1 SPACE is a translation of the term T1-Raum
introduced in P. Alexandroff and H. Hopf’s Topologie (1935). The letter is an abbreviation for
Trennungsaxiom (separation axiom) and Alexandroff and Hopf originally defined five such spaces
T0,..., T4 corresponding to different axioms. They associated
T0, T1 and T2 with Kolmogorov, Fréchet and Hausdorff respectively.
See Encyclopaedia of Mathematics.
TABLE in the sense of "an arrangement of numbers, words, or items of any kind, in a definite and compact
form, so as to exhibit some set of facts or relations in a distinct and comprehensive
way, for convenience of study, reference, or calculation."
The OED’s earliest quotation is from Chaucer’s Canterbury Tales c1386:
"Hise tables Tolletanes forth he brought Ful wel corrected."
Franklin’s Tale.
The Toletan tables were ‘the astronomical tables composed by
order of Alphonso X, king of Castile (1252-82), from their being adapted to the city of Toledo.’ (OED)
See MULTIPLICATION TABLE.
TAIL of a distribution appears in the writings of Karl Pearson although
the image probably presented itself to earlier workers: "... a
frequency-curve calculated from low moments fits best near the centre;
one calculated from high moments fits best near the tails of the
observation-curve." ("Contributions to the Mathematical Theory of Evolution"
Philosophical Transactions of the Royal Society. A, 185,
(1894), p. 108.) The term tail area seems to have come into circulation in the
1920s: see e.g. Karl Pearson’s "On a Method of Ascertaining Limits to
the Actual Number of Marked Members in a Population of Given Size from a
Sample," Biometrika, 20A, (1928) p. 171.
For "shorter" and "longer" tails see the entry on KURTOSIS. The terms "light" and "heavy" and
"thin" and "thick" entered currency in the 1970s (JSTOR search.)
TANGENT (in geometry). Tangents to a circle are treated in the propositions of
Book
III of Euclid’s Elements.
The Latin līnea tangens (touching
line) appears in Fincke’s Geometria
rotundi (1583). In
English the term “line tangent” appears in Thomas
Blundevil’s Exercises (1597) “Our moderne Geometricians haue of late inuented two other
right lines belonging to a Circle, called lines Tangent, and lines Secant.”
Blundevil also uses “tangent” as a noun: “Of
which Arke the line AD is the Tangent, and the line CD is the Secant thereof.”
(The citations are from the OED.)
TANGENT (in trigonometry). Bradwardine and other writers used
the term umbra versa.
Tangent was introduced by Thomas Fincke (1561-1656) in his
Thomae Finkii Flenspurgensis Geometriae rotundi libri XIIII,
Basileae: Per Sebastianum Henricpetri, 1583. He wrote tangens
in Latin.
Vieta did not approve of the term tangent because it could be
confused with the term in geometry. He used (c. 1593) sinus
foecundarum (abridged to foecundus) and also
amsinus and prosinus (Smith vol. 2, page 621).
According to the DSB, "Rheticus' Canon of the Doctrine of
Triangles (Leipzig, 1551) was the first table to give all six
trigonometric functions, including the first extensive table of
tangents and secants (although such modern designations were eschewed
by Rheticus as ’saracenic barbarisms')."
See Earliest Uses of Symbols of Trigonometry.
TANGRAM. The modern meaning of this term is a puzzle or square figure
divided into five triangles,
a square, and a rhomboid.
According to various dictionaries, the word may be derived from a Chinese word tang, or it may be derived
from the obsolete English word trangam, meaning a trinket or a gimcrack. Merriam-Webster says the word is of unknown origin.
Trangam is found in a 1658 dictionary.
On June 1, 1809, the American Citzien reported, “Vast numbers of those ‘tangrams and gimcracks’
are piled up in the office, of every shape and size, making
it a great toy shop. [Joel S. Berson]
A classified advertisement in the Franklin Gazette of Feb. 24, 1818, offers “Chinese Tangrams,” which were
probably puzzles [Bill Mullins].
According to Wikipedia and
this web page,
the word tangram was coined by Dr. Thomas Hill in 1848 for his book Geometrical Puzzles for the Young. [Perhaps
this is the first use of the word with its modern meaning.]
According to the same web page, the device was invented between 1796
and 1802 in China by Yang-cho-chu-shih, who published the book Ch'i
ch'iao t'u (Pictures using seven clever pieces).
The expression TAUBERIAN THEOREMS was introduced by G. H. Hardy and J. E. Littlewood in their
"Contributions to the Arithmetic Theory of Series," Proc. London Math. Soc. (2) XI. (1913), p. 411:
"The general character of the theorems which it [this paper] contains is
'Tauberian': they are theorems of the type whose first example was the
beautiful converse of Abel’s theorem originally proved by Tauber." The reference is to
Alfred
Tauber "Ein Satz aus der Theorie der unendlichen Reihen" Monatsch. für Math.,
8, (1897) 273-277. Norbert Wiener judged the work of Hardy and
Littlewood such an advance on that of Tauber that, "I feel it would be far more
appropriate to term these theorems Hardy-Littlewood theorems, were it not that
usage has sanctioned the other appellation." ("Tauberian Theorems,"
Annals of Mathematics, 2nd Ser., 33, No. 1. (Jan., 1932), 1-100.
See the article Tauberian theorems.
This entry was contributed by John Aldrich. See also HARDY-LITTLEWOOD THEOREM.
TAYLOR’S FORMULA, SERIES, THEOREM etc. are terms associated with propositions in
Brooke Taylor’s
Methodus incrementorum directa et inversa (1715), a book on what came to be called the CALCULUS OF FINITE DIFFERENCES.
Taylor did not consider questions of convergence—that came much
later—and the modern distinctions between formula, series and theorem were not
registered.
Kline (pp. 441-2) states that Taylor’s result was known to Gregory and Leibniz and
John Bernoulli published “practically the same result in 1694.” In the English
literature the theorem was attributed to Taylor: Colin Maclaurin wrote in his Treatise of Fluxions (1742): “This theorem
was given by Dr. TAYLOR ...” French writers also attributed the result to
Taylor, including Condorcet in 1784 and L'Huillier in 1786: the latter writes
in his Exposition
élémentaire des principes des calculs supérieurs about “le beau théorème que Taylor a le premier développé” (p. 47)
and refers to “le théorème de Taylor” (p. 207).
English writers of the early 19th century modelled their expositions on the French. Taylor’s theorem appears in
English in the 1816 translation of Lacroix’s Traité élémentaire
de calcul différentiel et de calcul intégral (1797-1800): “This formula is called Taylor”s Theorem, from the English
geometer by whom it was discovered.” (OED). Taylor’s series appears in 1819 in Thomas
Leybourn’s New Series of the Mathematical
Repository (p. 103): “Re-searches into some points of the theory of
derivative functions, which lead to a new demonstration of TAYLOR’s series, and
to the finite expression for the terms which are neglected, when the series stops
at any term, by AMPERE.” (The book is available on Google Book Search.)
[John Aldrich, Judith V. Grabiner, Julio
González Cabillón]
TENSOR was one of the family of terms introduced by William Rowan Hamilton (1805-1865) in his study of QUATERNIONS.
VECTOR and SCALAR and VERSOR were among the others. The tensor is for quaternions what the
MODULUS is for complex numbers. The term derives from the Latin tendĕre to stretch.
In 1846 Hamilton wrote in The London, Edinburgh, and Dublin Philosophical Magazine XXIX. 27:
Since the square of a scalar is always positive, while
the square of a vector is always negative, the algebraical excess of the former
over the latter square is always a positive number; if then we make (TQ)2 = (SQ)2 — (VQ)2, and if we suppose TQ to be always a real
and positive or absolute number, which we may call the tensor of the quaternion
Q, we shall not thereby diminish the generality of that quaternion. This tensor
is what was called in former articles the modulus.
The passage is reproduced in Section 19 of “On
Quaternions”. This ‘article’ is a compilation of 18 short papers
published in the Philosophical Magazine between 1844 and 1850 made by the editors of Hamilton’s Mathematical Papers. The editors
concatenated them to form a seamless whole, with no indication as to how the
material was distributed into the individual papers.
Tensor in Hamilton’s sense is no longer used.
[Information for this article was provided by David Wilkins and Julio González Cabillón.]
TENSOR, TENSOR ANALYSIS, TENSOR CALCULUS, etc. are 20th century
terms associated with the ABSOLUTE DIFFERENTIAL CALCULUS developed by
Ricci-Curbastroin
the 1880s and -90s on the basis of earlier work by Riemann,
Christoffel,
Bianchi and others. See Kline ch. 37 “The Differential Geometry
of Gauss and Riemann” and ch. 48 “Tensor Analysis and
Differential
Geometry.”
Ricci’s most influential publication was a substantial
article written with his former student Levi-Civita.
The article by the two Italians was written in French and appeared in the
leading German mathematical journal: “Méthodes de calcul différentiel absolu et leurs
applications,”
Mathematische Annalen, 54 (1901), p.
125-201. The word tensor does not appear: Ricci and Levi-Civita write about systèmes. Tensor is due to the well-known
Goettingen physicist Woldemar Voigt (1850-1919), who used it in his Die fundamentalen physikalischen Eigenschaften der
Krystalle in elementarer Darstellung of 1898 (OED and Julio González Cabillón).
Critically tensor was the term adopted by
Einstein and
Grossmann
in their first publication on general relativity, Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie
der Gravitation (Outline of a
Generalized Theory of Relativity and of a Theory of Gravitation)
(1913). Einstein made the subject fashionable. MacTutor relates that on a visit
to Princeton in 1921 he commented on the large audience his lecture attracted:
“I never realised that so many Americans were interested in tensor analysis.”
See also MacTutor:
General Relativity.
The OED reports that tensor analysis is
found in English in 1922 in H. L. Brose’s translation of Weyl’s Space-Time-Matter (Raum, Zeit, Materie): “Tensor analysis
tells us how, by differentiating with respect to the space co-ordinates, a new
tensor can be derived from the old one in a manner entirely independent of the
co-ordinate system. This method, like tensor algebra, is of extreme
simplicity.” The phrase tensor calculus appears in the same book. When
Levi-Civita’s Lezioni di
calcolo differenziale assoluto was translated into English in 1926, its
title included an explanation: The Absolute
Differential Calculus (Calculus of Tensors).
[This entry was contributed by John Aldrich.]
The term TERAGON was coined by Mandelbrot, according to
an Internet web page.
TERMINATING DECIMAL is found in 1804 in The Mathematical Repository by T. Leybourn:
“It has been shown that a whole number, having no integral root, has no
terminating decimal root....” [James A. Landau]
Finite decimal appears in
1850 in Arithmetic on the productive system, accompanied by a key and cubical blocks by Roswell C. Smith:
"17. REPEATING DECIMALS are also called INFINITE DECIMALS, those that terminate, or come
to an end, FINITE DECIMALS" [University of Michigan Digital Library].
TESSELLATION is found in 1660 in The History of the
Propagation and Improvement of Vegetables by Robert Sharrock
(1630-1684): "Yet they, instead of those elegant Tessellations, are
beautified otherwise in their site with as great curiosity."
The OED2 shows numerous citations in the 1800s of the spellings
tesselation, tesselated, and tesselate, and some modern
U. S. dictionaries show these as alternate spellings.
TESSERACT was used in 1888 by Charles Howard Hinton
(1853-1907) in A New Era of Thought (OED2). According to an
Internet site, Hinton coined the term.
The term TEST OF INDIVIDUAL EQUIVALENCE RATIOS was coined by
Anderson & Hauck (1990), according to an Internet web page by J. T.
Gene Hwang.
TETRAHEDRON is found in English in Sir Henry Billingsley’s
1570 translation of Euclid’s Elements (OED2).
TETRATION, a term for repeated exponentiation, was introduced
by Reuben Louis Goodstein. In "Transfinite ordinals
in recursive number theory, " Journal of Symbolic Logic 12 (1947),
he writes "... defines
successive new processes (which we may call tetration, pentation,
hexation, and so on)" [Samuel S. Kutler, Dave L. Renfro].
THEOREM. In Euclid 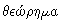 is a proposition to be proved.
It comes from an older word meaning “to look at” and related modern English
words include “theatre” and “theory.” (From Schwartzman and the OED.)
The word was adopted in Late Latin and French before being taken into English.
is a proposition to be proved.
It comes from an older word meaning “to look at” and related modern English
words include “theatre” and “theory.” (From Schwartzman and the OED.)
The word was adopted in Late Latin and French before being taken into English.
The earliest citation given by the OED for the word in English is in 1551 in
The Pathwaie to Knowledge by Robert Recorde: “Argts., The
Theoremes, (whiche maye be called approued truthes) seruing for the due
knowledge and sure proofe of all conclusions...in Geometrye.” In
the first
English translation of Euclid, which appeared in 1570, Billingsley
writes “A Theoreme, is a proposition, which requireth the
searching out and
demonstration of some propertie..of some figure.”
THEOREMA EGREGIUM is the name given to a theorem of Gauss to the
effect that the measure of curvature does not change if the surface is
transformed by a distance-preserving transformation. Gauss applied the
adjective himself in the “Disquisitiones
generales circa superficies curvas” (1827): see Gauss
Werke 4, p. 237.
The adjective is rendered as “remarkable” in
General investigations of
curved surfaces translated by Morehead and Hiltebeitel p. 20.
The term THEORY OF CLOSEDNESS was introduced in 1910 by
Vladimir Andreevich Steklov (1864-1926) (DSB).
THEORY OF GAMES appears in the title
"La théorie
du jeu et les équations intégrales à noyau symétrique," by Emile Borel, Compt. Rend. Acad. Sci.,
(Dec. 19, 1921) pp. 1304-8.
The term Theorie der Gesellschaftsspiele appears in
1928 in the title, "Zur Theorie der Gesellschaftsspiele" by J. von Neumann,
Math. Ann., 100,
295-320. Gesellschaftsspiele is translated as "parlor
games" by Kramer [James A. Landau].
Referring to the 1928 paper, von Neumann’s collaborator Herman
H. Goldstine wrote in The Computer from Pascal to von Neumann (1972):
This was his first venture in the field [of game theory],
and while there had been other tentative approaches --- by Borel, Steinhaus,
and Zermelo, among others --- his was the first to show the relations between
games and economic behavior and to formulate and prove his now famous minimax
theorem which assures the existence of good strategies for certain important
classes of games.
The English term, theory of games, appears in 1944
in the title Theory of Games and Economic Behavior by John von Neumann
and Oskar Morgenstern. This work established the theory of games as a major
subject. [James A. Landau].
Game theory appears in 1946-47 in Carl Kaysen, Review of
Economic Studies XIV. 14: "It is extremely doubtful whether the
degree of restriction of possible solutions offered by the ’solution'
of game-theory will be great enough to be of much practical value in
really complex cases" [Fred Shapiro].
THEORY OF NUMBERS. See NUMBER THEORY.
THEORY OF PROBABILITY. See PROBABILITY.
THEORY OF TYPES is found in Bertrand Russell, "Mathematical
Logic as Based on the Theory of Types," American Journal of
Mathematics 30 (1908) [James A. Landau].
THRACKLE and the THRACKLE CONJECTURE date from the 1960s to
speculations by John Horton Conway. For an explanation see the Wikipedia entry
Conway’s
thrackle conjecture.
The word thrackle is not in the OED and
Dan Archdeacon’s
site quotes Conway’s account of its origin:
When I was a teenager, on holiday with my
parents in Scotland, we once stopped to ask directions of a man who was fishing
by the side of a lake. He happened to mention that his line was thrackled. I'd
previously called this kind of drawing a tangle, but since I'd just found a
knot-theoretical use for that term, I changed this to thrackle. Several people
have told me that they've searched in vain for this word in dialect
dictionaries, but since I quizzed the fisherman about it, I'm sure I didn't
mishear it; he really did use it.
[This entry was contributed by John Aldrich.]
The use of the designations TIME DOMAIN and FREQUENCY DOMAIN to distinguish the correlation
and the spectral approaches to filtering theory, and to time series analysis generally, seems to have originated
in communication engineering.
"Frequency domain" appears in L. A. Zadeh’s "Theory of Filtering" (Journal of the Society for Industrial and
Applied Mathematics, 1, (1953), 35-51).
"Time domain" and "frequency domain" appear together in W. F. Trench’s "A General Class of Discrete Time-Invariant
Filters," Journal of the Society for Industrial and Applied Mathematics, 9, (1961), 405-421.
The terms soon became established in statistical time series analysis, see e.g. M. Rosenblatt & J. W. Van
Ness’s "Estimation of the Bispectrum," Annals of Mathematical Statistics, 36, (1965), 1120-1136
[John Aldrich].
TIME SERIES and TIME SERIES ANALYSIS. The term “time
series” appears in W. M. Persons’s “The Correlation of Economic
Statistics,” Publications of the
American Statistical Association, 12, (1910), 287-322. The phrase “time series analysis” entered circulation at the
end of 1920s, e.g. in S. Kuznets’s “On the Analysis of Time Series,”
Journal of the American Statistical Association, 23, (1928), 398-410, but it only
became really popular much later [John Aldrich].
Entries on Time Series topics include ABBE-HELMERT CRITERION, AUTOCORRELATION, AUTOREGRESSION,
BOX-JENKINS, CORRELOGRAM, MOVING AVERAGE, SAMPLE PATH, SERIAL CORRELATION,
SPECTRUM, TIME DOMAIN, TREND. See also the
full
list of Probability and Statistics entries.
The term TITANIC PRIME (a prime number with at least 1000
decimal digits) was coined in 1984 by Samuel D. Yates (died, 1991)
of Delray Beach, Florida ["Sinkers of the Titanic", J. Recreational
Math. 17, 1984/5, p268-274]. Yates also coined the term gigantic
prime in the mid-1980s, referring to a prime number with at least
10,000 decimal digits. [The term megaprime refers to a prime
of at least a million decimal digits.]
TOPOLOGY and TOPOLOGICAL. These terms came into wide use only in the 1930s, although the name topology
had been coined in the 19th century, topological results obtained
in the 18th and the study projected in the 17th. See MacTutor
History of Topology.
The earliest reference in Kline’s account of the history of topology (ch. 50, p. 1163) is to
Leibniz’s
Characteristica Geometrica of 1679. On Kline’s reading, "to the extent
that he was at all clear, Leibniz envisioned what we now call combinatorial
topology." On the other hand, M. J. Crowe A History of Vector Analysis
interprets the same work as an envisioning of vector analysis! Leibniz called
the study analysis situs or geometria situs.
Work from the 17th and 18th centuries,
now be classified as topological, include the EULER-DESCARTES RELATION
V + F - E = 2 for polyhedra and the KÖNIGSBERG BRIDGE PROBLEM. When
Euler
wrote about the latter he began by referring to Leibniz:
The branch of geometry that deals with magnitudes has been
zealously studied throughout the past; but there is another branch that has
been almost unknown up to now; Leibnitz spoke of it first, calling it the "geometry
of position" (geometria situs). This branch of geometry deals with relations
dependent on position alone, and investigates the properties of position; it
does not take magnitudes into consideration, nor does it involve calculation
with quantities.
(For publication details see the entry KÖNIGSBERG BRIDGE PROBLEM.)
The word TOPOLOGY was introduced in German in 1847 by
Johann
Benedict Listing (1808-1882) in "Vorstudien zur Topologie," Vandenhoeck
und Ruprecht, Göttingen, pp. 67, 1848. However, Listing had already used the
word for ten years in correspondence. Listing wrote about the EULER-DESCARTES RELATION
and about the MÖBIUS STRIP.
Topology is found in English
in February 1883 in Nature: "The term Topology was introduced by
Listing to distinguish what may be called qualitative geometry from the ordinary
geometry in which quantitative relations chiefly are treated" (OED2).
Listing, however, was not a major contributor to the field he named and
the major contributors of the 19th century favoured
Leibniz’s term analysis situs.
Riemann
revived the term (see section 2 of his Theorie der Abel’schen Functionem (1857)
Werke
p. 92) and Poincaré,
the most important contributor of the 19th century, also used it.
Poincaré’s first big paper on the subject was "Analysis Situs,"
Journal de l’École Polytechnique, 1, (1892) 1-121; a short
communication is available on-line, "Sur L’Analysis Situs,"
Comptes Rendus, 115, (1892), 633-636.
Analysis situs was the title of
Dehn and
Heegaard’s
survey in the Encyklopädie
der mathematischen Wissenschaften (1907, p. 153) and of
O. Veblen’s
American Mathematical Society Colloquium lectures (1922).
In the first decades of the 20th century the adjective
TOPOLOGICAL was more used than the noun. Thus the expression
"topological point of view" appears in O. Veblen & J. W. Alexander "Manifolds of N Dimensions,"
Annals of Mathematics, 14, (1912 - 1913), p. 163 as a variation on "point
of view of analysis situs." (JSTOR search.)
The term TOPOLOGICAL SPACE (topologischer Raum) was coined by
Hausdorff
and appears in his book on set theory (and analysis), Grundzüge der Mengenlehre
(1914, p. 211). The same work discusses METRIC SPACES.
By 1930 the term analysis situs was dead and in 1930-5
major works appeared in English, French and German called TOPOLOGY:
Lefschetz Topology (1930),
Kuratowski
Topologie I (1933) and
Alexandroff
& Hopf
Topologie (1935).
Hausdorff’s definition, however, is not equivalent to what is now known as
topological space; what he called Topologischer Raum is, in present day
terminology, a Hausdorff space since he includes the separation axiom T2 in
his definition. In his later book Mengenlehre (1927), Hausdorff discusses
various separation axioms, adding that
“...und wenigstens eins der Trennungsaxiome ist wohl das Minimum
dessen, was man von einem topologischen Raum fordern muß, wenn er nicht gar zu
abnorm ausfallen soll.” (...at least one of these seems to be the
minimum to be required so that a topological space shall not turn out too
abnormal). In this book, he does not attempt to fix the concept in a definitive
manner. The present usage of the term TOPOLOGICAL SPACE (topologischer Raum) was
firmly established in the German language textbook Topologie I (1935) by
Alexandroff and Hopf where they use what they call KURATOWSKI’S AXIOMS; they are
equivalent to Hausdorff’s axioms without axiom T2 which is then discussed
separately, along with other separation axioms. [Peter Flor]
The terms TOPOLOGICAL ALGEBRA and TOPOLOGICAL GROUP
were coined by David
van Dantzig. The first appears in the title of his 1931 Ph. D. dissertation
“Studiën over topologische Algebra” (DSB) and the second in his
“Ueber
topologisch homogene Kontinua” in Fundamenta
Mathematicae vol. 15 (1930) pages 102-125. In a footnote van
Dantzig states that this notion is essentially the same notion as that of a
“limesgruppe” which is said to be introduced by Otto Schreier
(1901-1929) in Abstrakte Kontinuierliech Gruppen (Abh. Math. Sem. Hambirg 4
(1925) 15-32) [Michael van Hartskamp].
TORSION. According to Howard Eves in A Survey of
Geometry, vol. II (1965), “The name torsion was introduced
by L. I. Valleé in 1825, replacing an older name
flexion” [James A. Landau].
TORSION as used in group theory: an element of a
group G is a torsion element if it generates a finite subgroup of G. An abelian
group consisting entirely of torsion elements is called a torsion group. In
any abelian group, the torsion elements form a subgroup, frequently called the torsion
subgroup of G. An abelian group is torsion-free if the neutral
element is its only torsion element.
This terminology seems to have arisen around 1930. Its
origin lies in algebraic (or combinatorial) topology. Poincaré (Second
complément à l´Analysis Situs, Proc. London Math. Soc, vol. 32 (1900),
277-308) defined torsion coefficients for manifolds (variétés), and he
distinguished manifolds with and without torsion. In a later terminology, his
torsion coefficients are structure constants of homology groups. In 1935, the
textbook Topologie I by Alexandroff-Hopf has the following concept of
torsion: “The elements of finite order of the r-th Betti group of E form
a subgroup called the r-th torsion group of E.” Here, the use of the
word torsion group is still tied to a topological context even though
the concept of a torsion subgroup seems to be hinted at. In the group
theoretical chapter of this book, the word torsion is not used. But in the same
year 1935, the paper Countable torsion groups by Leon Zippin (Annals of
Math. 36, 86-99) contains the following definition: “A torsion group T is a
discrete countable abelian group, every element of which is of finite order” -
quite the modern definition, except for the restriction to countable groups. Two
years before, Ulm (Zur Theorie der abzählbar-unendlichen Abelschen Gruppen, Math.
Annalen 107, pp. 774-803) did not yet use these terms, writing instead “groups
all of whose elements have finite exponents.” The torsion terminology was slow
in obtaining general acceptance; it was frequently used in research papers in
the 1940s, and is applied consistently in Kaplansky’s Infinite Abelian
Groups of 1954, while on the other hand, Marshall Hall’s textbook on group
theory, published in 1959, introduces the term “periodic group,” explaining
that “the term torsion group is used in certain applications.” The influential
book on topological groups, Abstract Harmonic Analysis I by Hewitt and
Ross (1963) uses the torsion terminology and may have been important in
promoting it.
[This entry was contributed by Peter Flor.]
TORUS. Hero mentions a mathematician named Dionysodorus as the
author of On the Tore, in which a formula for the volume of
the torus is given [DSB].
An early use of torus as a mathematical term in English is in
1860 in The Practical Draughtsman’s Book of Industrial Design
by William Johnson: “In geometry, the torus is a solid, generated by a circle,
revolving about an axis, continuing constantly in the
plane of this axis, in such a manner, that all sections
made by planes passing through the axis are equal circles,
and all sections by planes perpendicular to the axis will
also be circles, but of variable diameters.” [Google print search]
TOTIENT. E. Prouhet used indicateur (indicator) in 1846
in Nouv. Ann. de Math. V. 176.
Totient was introduced by Sylvester in "On Certain Ternary Cubic-Form Equations",
Amer. J. Math 2 (1879) 280-285, 357-393, in Sylvester’s Collected Mathematical Papers
vol. III p. 321. He writes: "The so-called (phi) function of any number I shall
here and hereafter designate as its (tau) function and call its
Totient." This information was taken from a post in sci.math by
Robert Israel.
See Euler’s φ function on Earliest Use of Symbols of Number Theory.
TOWER OF HANOI. The Tower of Hanoi puzzle was published by
Edouard Lucas
in 1883. Lucas published it under the name of M. Claus, an anagram of Lucas.
See Paul K. Stockmeyer’s page.
TRACE (of a matrix) is a translation of the German die Spur (related to the English word
"spoor.") In his 1922 translation of H. Weyl’s Raum, Zeit, Materie (Space-Time-Matter) H. L.
Brose writes: "the trace (spur) of a matrix." Some writers in English preferred the term "spur," e.g.
A. C. Aitken Determinants and Matrices (9th edition 1956) writes "the spur or trace of A. We
shall denote it by sp A."
The TRACTRIX was named by Christiaan Huygens (1629-1695) in 1692, according to the
University of St. Andrews website.
The OED quotes the entry from Chambers Cyclopædia (1727-41),
"Tractrix, in geometry, a curve line, called also catenaria."
[Error: the tractrix is the involute of the catenary, not the catenary itself.]
In Webster’s 1828 dictionary, the word is spelled tractatrix,
with the middle syllable stressed.
TRAMCAR PROBLEM also called NEWMAN’S TRAMCAR PROBLEM. In the Theory of Probability (1939, p. 186)
Harold Jeffreys writes, “The following problem was suggested to me several years ago by Mr
M. H. A. Newman.
A man travelling in a foreign country has to change trains at
a junction, and goes into the town, the existence of which he has only just
heard. He has no idea of its size. The first thing that he sees is a tramcar
numbered 100. What can he infer about the number of tramcars in the town? It
may be assumed for the purpose that they are numbered consecutively from 1
upwards.”
TRANSCENDENTAL. Leibniz coined the word transcendental in mathematics, using
transcendens in the fall of 1673 in Progressio figurae segmentorum
circuli aut ei sygnotae.
Leibniz used curvae transcendentes and figurae transcendentes
in December 1674 in De progressionibus et geometria arcana et methodo tangentium inversa.
Leibniz used aequatio transcendens in 1676 in Series convergentes duae.
[This information was provided by Siegmund Probst, who reports that these Leibniz papers
can be viewed at an archive of publications by Leibniz at
http://www.nlb-hannover.de/Leibniz/Leibnizarchiv/Veroeffentlichungen/].
According to Paulo Ribenboim in My Numbers, My Friends,
"LEIBNIZ seems to be the first mathematician who employed the expression
'transcendental number' (1704)."
Euler used transcendental in his 1733 article in Nova
Acta Eruditorum titled "Constructio aequationum quarundam differentialium
quae indeterminatarum separationem non admittunt":
Now there are kinds of constructions, which can be called transcendental,
which arise in solving differential equations and cannot be transformed into
algebraic equations.
The above citation and translation were provided by Ed Sandifer.
Euler used a phrase which is translated transcendental
quantities in 1745 in Introductio in analysin infinitorum
[James A. Landau]. Euler wrote that these numbers "transcend the
power of algebraic methods" (Burton, p. 603). He also used the term
in the title "De plurimis quantitatibus transcendentibus, quas nullo
modo per formulas integrales exprimere licet," which was presented in
1780 and published in 1784 in Acta Academiae Scientarum Imperialis
Petropolitinae.
Transcendental function appears in 1809 in the title
"Théorie d'un nouvelle fonction transcendente" by Soldner.
Transcendental curve is found in English in 1811 in C. Hutton,
Course Math. III.: “Transcendental or mechanical curves,
are such as cannot be ... expressed by a pure algebraical equation. Thus, y
= log x, y = A sin x, ... y = Ax, are equations to transcendental curves.” [OED]
Transcendental equation is found in English in
1813 in Pantologia. A new cabinet cyclopædia, by John Mason Good, Olinthus Gilbert Gregory, and N. Bosworth
[Google print search]
Transcendental quantity appears in 1820 in
A Collection of Examples of the Applications of the Differential and Integral Calculus
by George Peacock
In 1828, in Elements of Geometry and Trigonometry (1832)
by David Brewster (a translation of Legendre), the term
transcendental is not used in this passage:
It is probable that this number π
is not even included among algebraical irrational
quantities, in other words, that it cannot be the root of an
algebraical equation having a finite number of terms with rational
co-efficients: but a rigorous demonstration of this seems very
difficult to find; we can only show that the square of π is also an irrational number.
Transcendental number appears (as transscendente Zahl)
in 1882 in "Ueber die Zahl  " by F.
Lindemann.
" by F.
Lindemann.
Transcendental number appears in English in
a lecture delivered on Sept. 4, 1893, "The Transcendency of the Numbers e and π," found in
Lectures on Mathematics: Delivered from Aug. 28 to Sept. 9, 1893, Before Members of the Congress of Mathematics
by Felix Klein: "The proof that π is a transcendental number will forever mark an epoch in
mathematical science." [Google print search]
Transcendental irrational is found in 1902 in The
Number-System of Algebra by Henry B. Fine (and may occur in the
earlier 1891 edition): "This number e, the base of the
Naperian system of logarithms, is a "transcendental" irrational,
transcendental in the sense that there is no algebraic equation with
integral coefficients of which it can be a root."
In 1906 in History of Modern Mathematics, David Eugene Smith
refers to transcendent numbers.
Webster’s unabridged 1913 dictionary has: "In mathematics, a
quantity is said to be transcendental relative to another
quantity when it is expressed as a transcendental function of the
latter; thus, ax, 102x, log x,
sin x, tan x, etc., are transcendental relative
to x.
TRANSFINITE. Georg Cantor (1845-1918) used this word in the title of a paper published in 1895,
"Beiträge zur Begründung der Transfiniten Mengenlehre"
Mathematische Annalen, 46,
p. 481 The English word appears in Bertrand Russell’s Principles of Mathematics.
The OED quotes from a review of this work in Nature
(1903) 3 Sept. 411/2 "To readers unacquainted with [Cantor’s] 'Mengenlehre',
the introduction of transfinite numbers must appear rather startling."
TRANSITIVE. (Of a binary relation)
Bertrand Russell wrote in "On the Notion of Order," Mind, 10, (1901), p. 32. "When
ARB and BRC imply ARC, I call R transitive .... This term was used in this
sense by De Morgan ... It is now generally adopted." De Morgan wrote in "On
the Symbols of Logic, the Theory of the Syllogism, and in particular of the
Copula," Transactions of the Cambridge Philosophical Society, 9,
(1850) p. 104: "The first is what I shall call transitiveness, symbolized
in X—Y—Z = X—Z; meaning that if X stand in the relation
denoted by — to Y, and Y to Z, X therefore stands
in that relation to Z." (OED)
TRANSPOSE (noun, of a matrix).
Transposed matrix appears in 1858 in A. Cayley "A Memoir on the Theory of Matrices"
Phil.
Trans. R. Soc. CXLVIII, p. 32:
Coll
Math Papers, I, 475-96 "A matrix compounded with the transposed matrix gives rise to a symmetrical matrix" (OED2).
Transpose is found 1937 in Mod. Higher Algebra by A. A. Albert: "Every square matrix is similar
to its transpose" (OED2).
TRANSPOSITION (for a two-element cycle) is found in Cauchy’s 1815 memoir
"Sur le nombre des valeurs q'une fonction peut acquérir lorsqu'on permute de
toutes les manières possibles les quantités qu'elle renferme" (Journal de
l'Ecole Polytechnique, Cahier XVII = Cauchy’s Oeuvres, Second series, Vol.
13, pp. 64--96.) This usage was found by Roger Cooke, who believes this is the first
use of the term.
TRANSVERSAL. In 1828 in Elements of Geometry and
Trigonometry (1832) by David Brewster (a translation of
Legendre), the line is referred to as "a third line" and as "the
secant line."
In Webster’s dictionary of 1828, the term is "the cutting
line."
Transversal is found in 1847 in Cayley, Camb. & Dubl. Math.
Jrnl. II. 52: "When three conics have the same points of
intersection, any transversal intersects the system in six points,
which are said to be in involution."
TRAPEZIUM and TRAPEZOID. The early editions of Euclid
1482-1516 have the Arabic helmariphe; trapezium is in
the Basle edition of 1546.
Both trapezium and trapezoid were used by Proclus (c.
410-485). From the time of Proclus until the end of the 18th century,
a trapezium was a quadrilateral with two sides parallel and a
trapezoid was a quadrilateral with no sides parallel. However,
in 1795 a Mathematical and Philosophical Dictionary by Charles
Hutton (1737-1823) appeared with the definitions of the two terms
reversed:
Trapezium...a plane figure contained under four
right lines, of which both the opposite pairs are not parallel. When
this figure has two of its sides parallel to each other, it is
sometimes called a trapezoid.
No previous use the words with Hutton’s definitions is known.
Nevertheless, the newer meanings of the two words now prevail in U. S.
but not necessarily in Great Britain (OED2).
Some geometry textbooks define a trapezoid as a quadrilateral with
at least one pair of parallel sides, so that a parallelogram is
a type of trapezoid.
TRAVELING SALESMAN PROBLEM. The first use of this term "may
have been in 1931 or 1932, when A. W. Tucker heard the term from
Hassler Whitney of Princeton University." This information comes from
an Internet web page, which refers to E. L. Lawler, J. K. Lenstra, A.
H. G. Rinnooy Kan, D. B. Shmoys, editors, The Traveling Salesman
Problem (1985).
Other terms are knight’s tour and the messenger problem.
The term TREATMENT for any stimulus that is applied
to observe the effect in an experiment was introduced, by R. A. Fisher in chapter
VIII, section 48, Technique of Plot Experimentation, of his
Statistical Methods
for Research Workers (1925). This was the first presentation of Fisher’s
theory of experimental design and several other terms were introduced there
as well.
The term TREE in graph theory was coined by James Joseph
Sylvester, according to an Internet web site.
Tree was used by Arthur Cayley in 1857 and appears in his
Mathematical Papers (1890) III. 242: "On the Theory of the
analytical Forms called Trees" (OED2).
TREND. According to the OED
trend was originally a geological term for "the way something [e.g. a
coast-line] trends or bends away" and then it acquired a figurative sense meaning
"the general course, tendency, or drift of action, thought etc." Statistical
writers used the word in this latter sense but R. H. Hooker
seemed to be aware he was extending the meaning when he wrote, "The
curve or line representing the successive instantaneous averages [moving-averages]
I propose to call the trend." See his "Correlation
of the Marriage-Rate with Trade," Journal of the Royal Statistical Society,
64, (1901), p. 486. W. I. King’s Elements
of Statistical Method (1912) took Hooker’s construction and the term "trend"
to a broader audience. The term was soon applied to curves or lines constructed
on other principles.
See also MOVING AVERAGE.
TRIANGLE. Three-sided figures are discussed in Book I of Euclid’s
Elements; Definitions 20 and 21
describe different kinds of triangles. The English word “triangle” appears in Sir
Henry Billingsley’s translation of the Elements (1570). However the OED finds earlier appearances in English,
including a passage from John de Trevisa’s translation of De Proprietatibus Rerum, “Some [nuts] ben distinguid in
þe cop as it were with
þe schap
of a triangle [orig. per formam trianguli]” (1398).
TRIANGLE INEQUALITY appears in 1921 in Albert A. Bennett "Normalized Geometric Systems,"
Proc. National Acad. Sci. U.S.A. 7 p. 88. (JSTOR)
Fréchet had drawn attention to this property of "l’écart" in his
Sur quelques points du calcul fonctionnel,"
Rendiconti del Circolo matematico di Palermo,
22, (1906) p. 30 but he did not give it a name. In his
Grundzüge der Mengenlehre (1914, p. 211) Hausdorff used the term "Dreiecksaxiom" (triangle axiom.)
See METRIC SPACE.
TRIANGULAR NUMBER. Vieta used the terms triangular,
pyramidal, triangulo-triangular, and triangulo-pyramidal
number.
Triangular (as a noun) appears in English in 1706 in
Synopsis Palmariorum Matheseos by William Jones (OED2).
The TRIDENT was named by Isaac Newton, according to John Harris
in Lexicon Technicum.
Eves (page 279) has, "The locus is a cubic that Newton called a
Cartesian parabola and that has also sometimes been called a
trident; it appears frequently in La géometrie.
TRIDIMENSIONAL and UNIDIMENSIONAL appear in Sir William
Rowan Hamilton, Lectures on Quaternions (London: Whittaker &
Co, 1853) [James A. Landau].
Tridimensional appears in the following sentence: "But there
was still another view of the whole subject, sketched not long
afterwards in another communication to the R. I. Academy, on which it
is unnecessary to say more than a few words in this place, because it
is, in substance, the view adopted in the following Lectures, and
developed with some fulness in them: namely, that view according to
which a QUATERNION is considered as the QUOTIENT of two directed
lines in tridimensional space."
Unidimensional appears in the following sentence: "It seemed
(and still seems) to me natural to connect this extra-spatial
unit with the conception [3] of TIME, regarded here merely as an
axis of continuous and uni-dimensional progression."
TRIGONOMETRIC EQUATION is found in English in 1855 in
A treatise on plane and spherical trigonometry
by William Chauvenet. In this book "trigonometric equations" is a chapter title
but the term does not appear in the running text [University of Michigan Digital Library].
The term TRIGONOMETRIC FUNCTION was introduced in 1770 by Georg
Simon Klügel (1739-1812), the author of a mathematical dictionary
(Cajori 1919, page 234).
TRIGONOMETRIC LINE. Vincenzo Riccati (1707-1775) "for the
first time used the term 'trigonometric lines' to indicate circular
functions" in the three-volume Institutiones analyticae
(1765-67), which he wrote in collaboration iwth Girolamo Saladini
(DSB).
TRIGONOMETRIC SERIES. Trigonometrical series is found in 1843 in
The Penny Cyclopædia of the Society for the Diffusion of Useful Knowledge.
[Google print search]
Trigonometric series is found in English in 1855 in
A treatise on plane and spherical trigonometry
by William Chauvenet. In this book "trigonometric series" is a chapter title
but the term does not appear in the running text [University of Michigan Digital Library].
The term TRIGONOMETRY is due to Bartholomeo Pitiscus
(1561-1613) and was first printed in his Trigonometria: sive de
solutione triangulorum tractatus brevis et perspicuus, which was
published as the final part of Abraham Scultetus' Sphaericorum
libri tres methodicé conscripti et utilibus scholiis
expositi (Heidelberg, 1595) (DSB).
The word first appears in English in 1614 in the English translation
of the same work: Trigonometry: or The Doctrine of Triangles.
First written in Latine, by B. Pitiscus..., and now Translated into
English, by Ra. Handson.
TRIMMING, TRIMMED MEAN, etc. are found in John W. Tukey’s
"The Future of Data Analysis," Annals of Mathematical Statistics,
33, (1962), pp. 1-67. Tukey writes that in problems of location "it is
natural to attempt to eliminate the effects of "wild shots" by trimming
each sample, by removing equal numbers of the lowest and highest observations,
and then proceeding as if the trimmed sample were a complete sample." (p. 17)
The same section contains a discussion of WINSORIZING.
(David 2001)
TRINOMIAL was used in English in 1674 in Arith. (1696)
Samuel Jeake (1623 - 1690): "If three Quantities be conjoyned, and but
three, they are sometime called Trinomials" (OED2). [According to
An Etymological Dictionary of the English Language (1879-1882),
by Rev. Walter Skeat, "Not a good form; it should rather have been
trinominal."]
TRISECTION appears in English in 1664 in Power, Exp.
Philos.: "The Trisection of an Angle" (OED2).
TRIVARIATE (in Statistics) appears in the phrase “trivariate distributions” in S. J. Pretorius “Skew Bivariate
Frequency Surfaces, Examined in the Light of Numerical
Illustrations,” Biometrika, 22, (1930), p. 138. (JSTOR search)
See BIVARIATE, N-VARIATE, TRIVARIATE and UNIVARIATE.
TRIVIAL (deriving from trivium, for which see LOGIC)
has become a term of art in mathematics.
In “Deuxième mémoire sur les fonctions doublement
périodiques,” Journal de Mathématiques Pures et
Appliquées, tom. xix. (1854), pp. 193-208, Cayley wrote,
“Je suppose d'abord que 2k + 1 soit égal à l'unité, transformation que l'on peut nommer triviale.”
[I first suppose that 2k + 1 may be equal to unity, a transformation that one could call “trivial.”]
In “A Second Memoir Upon Quantics,” Philosopohical Transactions of the Royal Society of London (1856), Cayley
wrote in a footnote: “It is hardly necessary to remark, that the multipliers ... and generally any coefficients or
quantities not expressly stated to contain the set {a, b, c, ...}, are considered as independent of the set, or
to use a convenient word, are considered as ‘trivials.’”
The OED illustrates
with the following quotations: R. D. Carmichael Diophantine Analysis
(1915, p. 28) "We have thus established the fact that Eq. (2) has at least one
integral solution which is not trivial." G. Birkhoff & S. MacLane Survey
of Modern Algebra (1941, p. 135) "The reflexive property is trivial (every
group is isomorphic to itself by the identity transformation)."
[John Aldrich, James A. Landau]
TROCHOID was coined by Gilles Persone de Roberval (1602-1675)
(Smith vol. I, page 385; Cajori 1919, page 162).
TROY WEIGHT. This term is believed to derive from the name of
the city of Troyes, France. The OED shows a use of “marc. de
troye” in 1390-91
and troy weyght in about 1500.
The terms TRUNCATED CUBE, TRUNCATED OCTAHEDRON, TRUNCATED
ICOSAHEDRON, and TRUNCATED DODECAHEDRON are all due to
Johannes Kepler. He used cubus simus and dodekaedron
simum in Harmonice Mundi (1619).
TRUNCATION (in statistics). See CENSORING.
TRUTH SET is found in 1940 in Mathematical logic by
Willard Van Orman Quine: “A truth set S of φ
will include..anywhere from all to none of the ultimate truth-functional
components..of φ.” [OED]
The term TRUTH TABLE was used by Emil Leon Post
(1897-1954) in the title “Determination of all closed systems of truth tables”
(abstract of a paper presented at the 24 April 1920 meeting of the American
Mathematical Society), Bulletin of the American Mathematical Society 26.
Post also used the term in “Introduction to a General
Theory of Elementary Propositions” American Journal of Mathematics, 43,
(1921), p. 167:
So corresponding to each of the 2n
possible truth-configurations of the p’s a definite truth-value of f
is determined. The relation thus effected we shall call the truth-table of f.
The same concept was introduced by Ludwig
Wittgenstein (1889-1951) as Wahrheitstafel in his Tractatus
Logico-Philosophicus (1921). In the facing English version the word is
translated as truth table.
This entry was contributed by James A. Landau and John Aldrich.
TRUTH VALUE. Gottlob Frege (1848-1925) used the term
Wahrheitswert in 1891 in Funktion, Begriff, Bedeutung
(1975): "Ich sage nun: 'der Wert unserer Funktion ist ein
Wahrheitswert' und unterscheide den Wahrheitswert des Wahren von dem
des Falschen."
In English, truth value is found in 1903 in Principles
of Mathematics by Bertrand Russell: “There are, we are told.., three
elements in judgment: (1) the recognition of truth, (2) the Gedanke, (3) the truth-value (Wahrheitswerth).” [OED]
TSCHIRNHAUS' CUBIC appears in R. C. Archibald’s paper
written in 1600 where he attempted to classify curves, according to
the University of St. Andrews website.
The term TURING MACHINE appears in 1937 in A. Church’s
review of A. M.Turing’s
1937 paper "On Computable Numbers
with an Application to the Entscheidungsproblem": "Certain further
restrictions are imposed on the character of the machine, but these are of such
a nature as obviously to cause no loss of generality - in particular, a human
calculator, provided with pencil and paper and explicit instructions, can be
regarded as a kind of Turing machine." (Journal of Symbolic Logic, 2,
p. 42) (OED)
The term TURING TEST, referring to the procedure described in Turing’s "Computing Machinery
and Intelligence," Mind, 79, (1950), 433-460,
is apparently found in 1956 in
Mental Health Research Institute Staff Publications,
University of Michigan, Mental Health Research Institute, based on a Google print search which provides only snippet view:
“To check the validity of his claim he subjects it to the Turing test.
This is a hypothetical test in which both the behavior of a human and the
mechanical translator is presented to an impartial observer...”
The term seems to have entered currency in
the 1970s. A JSTOR search found it used in B. A. Farrell “On the Design of a Conscious Device,” Mind, 79,
(1970), p. 345.
See DECISION PROBLEM.
The term TWIN PRIME was coined in 1916 by Paul Gustav
Stäckel (1862-1919) in "Die Darstellung der geraden Zahlen als
Summen von zwei Primzahlen," Sitz. Heidelberger Akad. Wiss.
(Mat.-Natur. Kl.) 7A (10) (1916), according to Algorithmic Number
Theory by Bach and Shallit [Paul Pollack].
Twin-prime is found in English in 1930 in Number by T.
Dantzig: “ It has been shown that the so-called twin-primes, such
as (3,5), (5,7),..(41,43), etc., become rarer and rarer as the numbers
increase.” [OED]
TYPE I ERROR and TYPE II ERROR. In their first joint
paper "On the Use of Certain Test Criteria for Purposes of Statistical
Inference, Part I," Biometrika, (1928) 20A, 175-240 Neyman and
Pearson referred to "the first source of error" and "the second source of error" (David, 1995).
Errors of first and second kind
is found in 1933 in J. Neyman and E. S. Pearson,
"On the Problem
of the Most Efficient Tests of Statistical
Hypotheses," Philosophical Transactions of the Royal Society
of London, Ser. A (1933), 289-337 (David, 1995).
Type I error and Type II error are found in 1933 in J.
Neyman and E. S. Pearson, "The Testing of Statistical Hypotheses in
Relation to Probabilities A Priori," Proceedings of the
Cambridge Philosophical Society, 24, 492-510 (David, 1995).
Front -
A -
B -
C -
D -
E -
F -
G -
H -
I -
J -
K -
L -
M -
N -
O -
P -
Q -
R -
S -
T -
U -
V -
W -
X -
Y -
Z -
Sources
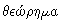 is a proposition to be proved.
It comes from an older word meaning “to look at” and related modern English
words include “theatre” and “theory.” (From Schwartzman and the OED.)
The word was adopted in Late Latin and French before being taken into English.
is a proposition to be proved.
It comes from an older word meaning “to look at” and related modern English
words include “theatre” and “theory.” (From Schwartzman and the OED.)
The word was adopted in Late Latin and French before being taken into English.
 " by F.
Lindemann.
" by F.
Lindemann.