Earliest Known Uses of Some of the Words of Mathematics (Z)
Last revision: Aug. 11, 2008
z-AXIS. Axis of z appears in "On the Attractions of Homogeneous Ellipsoids" by James Ivory,
Philosophical Transactions of the Royal Society of London, Vol. 99. (1809), pp. 345-372.
[JSTOR].
Axis z is found in 1866 in the 8th edition of
Elements of analytical mechanics
by William Holms Chambers Bartlett:
"Take the axis z as the axis of rotation; denote the angular velocity by
φ, and the distance of the particle M from the axis
z by r" [University of Michigan Digital Library].
The terms z and the z DISTRIBUTION were introduced by R. A. Fisher in
"On a Distribution Yielding the Error Functions of Several well Known Statistics",
Proceedings of the International Mathematics Congress, Toronto (1924). Fisher’s development of the analysis
of variance in this paper and in his book
Statistical Methods for Research Workers
(1925) was based on the z distribution. Fisher’s z is related to the
modern F by z = ½ ln F [James A. Landau].
See also F DISTRIBUTION and VARIANCE.
ZENO’S PARADOXES are due to
Zeno of Elea
(c. 490 BC - c. 425 BC) but none of his works survive and the paradoxes are known through the writings of Aristotle and
Simplicius,
a 6th century AD commentator on Aristotle. The four paradoxes, relating to motion, the dichotomy, the Achilles,
the arrow, and the stadium, are discussed in
Book VI of Aristotle’s
Physics.
For a brief account see Kline (35-37) and, for a much more detailed one,
Zeno’s Paradoxes
from the Stanford Encyclopedia of Philosophy.
The regular application of the word "paradox" is relatively recent;
before the 20th century "fallacy" or "argument" were more common.
Cajori’s 9-part "The History of Zeno’s Arguments
on Motion: Phases in the Development of the Theory of Limits," American Mathematical
Monthly, 22, (1915) shows that for most of their history the arguments
were held in low esteem but that in the 19th century their prestige
rose. Bertrand Russell wrote of Zeno, "Having invented
four arguments, all immeasurably subtle and profound, the grossness of subsequent
philosophers pronounced him to be a mere ingenious juggler, and his arguments
to be one and all sophisms." Principles of Mathematics (1903, p. 347)
This entry was contributed by John Aldrich. See PARADOX.
ZERMELO-FRAENKEL SET THEORY is found in the title "Ein
axiomatisches System der Mengenlehre nach Zermelo und Fraenkel," by
Ernst-Jochen Thiele, Z. Math. Logik Grundlagen Math. (1955).
The term is also found in R. Montague, "Zermelo-Fraenkel set theory
is not a finite extension of Zermelo set theory," Bull. Amer Math.
Soc. 62 (1956).
Attributions to Ernst Zermelo
"
Untersuchungen über die Grundlagen der Mengenlehre. I" Math. Annalen (1908) occur in
A. Fraenkel,
"
Zu den Grundlagen der Cantor-Zermeloschen Mengenlehre,"
Math. Annalen (1922) and "Über die Zermelosche Begründung der Mengenlehre,"
Jahresbericht der Deutschen Mathematiker-Vereinigung 30, 2nd section (1921) [James A. Landau].
ZERO, like its synonym CIPHER, derives from the
Sanskrit sunya. Smith and Karpinski give the derivation in their
The
Hindu-Arabic Numerals (1911). The first step was the
transcription of the Sanskrit word meaning “void” into Arabic as as-sifr or sifr. For the evolution of the symbol 0 see the entry on
Earliest Uses of Symbols for Constants.
The Arabic word was taken into Latin as zephirum in the Liber Abaci (1202) of
Leonardo of Pisa (1180-1250) (or Fibonacci). Referring to the symbol he wrote,
“...quod arabice zephirum appelatur.”
Smith
and Karpinsski (pp. 56-62) relate how some Italian works used “zeuro” and
“zepiro” and how the word “zero” is found in some 14th century
manuscripts. The word makes its first appearance in a printed work in De arithmetrica opusculum, by Filippo
Calandri, which was printed in Florence in 1491.
By 1515 the French word “zéro” had appeared
and the earliest citation in the OED for the English word zero is from Edward Grimstone’s 1604
translation of The Natural and Moral History
of the Indies from the Spanish of José de Acosta:
They accompted their weekes by thirteene dayes, marking the dayes with a Zero or cipher.
That alternative term cipher had been in English much longer. It also descended from sifr but via the mediaeval
Latin cifra and Old French cyfre. The OED has a quotation from 1399, from Richard the
Redeles (Richard without Counsel) a book of advice addressed to the
King:
Than satte summe, as siphre doth in awgrym, That noteth a place, and no
thing availith.
A later OED quotation gives the impression that “zero” was still seen as the exotic
newcomer in 1702:
Zero, a word sometimes used (particularly among the French) for a Cypher, or (0.)
From A Mathematical Dictionary by Joseph Raphson and Jacques Ozanam.
The word “cipher” was still current in the late 19th century: see James B. Thomson’s Complete
Graded Arithmetic (1882)
The last one is called Naught, because when standing alone it has no value. It is also called Cipher or Zero.
Today “cipher”
is no longer used in this sense but it survives in the derived senses of a
“nonentity” (dating from 1579) and “secret writing” (dating from 1528).
The word naught (or nought) has its origins in the Old English
word for nothing, nōwiht from the 9th century. The expression
“all for naught” has been in English since the 13th century. The earliest quotation in the OED
illustrating the use of the word for the figure representing 0 is from a
political tract by Milton written in 1649, “cast
away like so many Naughts in Arithmetick.”
ZERO (of a function) is found in 1893 in A Treatise on the
Theory of Functions by James Harkness and Frank Morley: "By a
zero of P(x) is meant a point at which
P(x) vanishes."
ZERO MATRIX appears in J. J. Sylvester "Note on the
Theory of Simultaneous Linear Differential of Difference Equations with Constant
Coefficients," American Journal of Mathematics, 4, (1881), 321-326,
Coll Math Papers, III, pp. 551-6. A. Cayley "A Memoir on the Theory of Matrices" (1858)
Coll Math Papers, I, p. 477 referred to the matrix zero.
ZERO-SUM GAME appears in 1944 in Theory of Games and
Economic Behavior by J. von Neumann and O. Morgenstern (David,
1998).
ZEROTH is found in 1850 in The calculus of operations
by John Paterson, A. M.:
"To show inductively that this law persists, we have constructed the following
table for ten successive units of time, in which the columns under
φ''' and φ'' are obtained,
the first, by multiplying AΦ''' by 3, 6 and 2
respectively for power of the second, first and zeroth order; and
the second, by multiplying AΦ'' by 4 and by 2 for
power of the first and of the zeroth order."
Zeroth is also found in 1893 in An
elementary treatise on Fourier’s series and spherical, cylindrical, and ellipsoidal
harmonics with applications to problems in mathematical physics by William Elwood Byerly:
"It is a finite sum terminating with the first power of x if
m is odd, and with the zeroth power of x if m is even"
[University of Michigan Digital Library, both citations].
The term ZETAIC MULTIPLICATION was coined by James Joseph
Sylvester.
Zeta-ic multiplication was used in 1840 and is found in
Sylvester’s Collected Mathematical Papers (1904) I. 47: "I use
the Greek letter 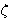 to denote that the product of factors to
which it is prefixed is to be effected after a certain symbolical
manner. This I shall distinguish as the zeta-ic product. ... Rule for
zeta-ic multiplication. Note. An analogous interpretation may be
extended to any zeta-ic function whatever" (OED2).
to denote that the product of factors to
which it is prefixed is to be effected after a certain symbolical
manner. This I shall distinguish as the zeta-ic product. ... Rule for
zeta-ic multiplication. Note. An analogous interpretation may be
extended to any zeta-ic function whatever" (OED2).
ZORN’S LEMMA, named after
Max Zorn (1906-1993),
has received plenty of attention from historians, perhaps because it illustrates the problems posed
by eponymous terms. See EPONYMY.
The publication history is fairly straightforward.
The "lemma" appears in "A remark on method in transfinite algebra,"
Bulletin of the American Mathematical Society, 41, (1935), 667-670,
although Zorn calls it a "maximum principle" and refers to it as an "axiom."
The phrase "Zorn’s lemma" first appears in print in John W. Tukey’s Convergence
and Uniformity in Topology (1940, p. 7), although there are four different
versions of it.
The historical context is discussed in Gregory Moore’s Zermelo’s
Axiom of Choice: Its Origins, Development and Influence (1982) and Paul
J. Campbell’s "The Origins of 'Zorn’s Lemma'," Historia Mathematica,
5, 1978, 77-89. Moore (p. 220) begins by saying, "The history of
maximal principles, such as Zorn’s Lemma, is strewn with multiple independent
discoveries of fundamentally similar propositions. ... Unlike many other multiple
independent discoveries, those involving maximal principles were in no sense
simultaneous, since they extended over three decades." This work of Moore
and Campbell prompts the question, why should Zorn’s work be recognised and
not the earlier work of
Hausdorff and
Kuratowski?
Who was responsible for the name "Zorn’s lemma"? In 1976 Campbell asked Zorn
and Tukey for their recollections. Tukey’s reply indicates that the term was
in circulation in Princeton before he wrote his book and he speculates that
Lefschetz introduced it there. Zorn says the name was already in circulation
before he presented his paper to the American Mathematical Society in October
1934! He thought he had probably first heard it from Øystein Ore.
Bill Dubuque, Julio González Cabillón and John Aldrich contributed
to this entry. See AXIOM OF CHOICE.
Front -
A -
B -
C -
D -
E -
F -
G -
H -
I -
J -
K -
L -
M -
N -
O -
P -
Q -
R -
S -
T -
U -
V -
W -
X -
Y -
Z -
Sources
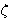 to denote that the product of factors to
which it is prefixed is to be effected after a certain symbolical
manner. This I shall distinguish as the zeta-ic product. ... Rule for
zeta-ic multiplication. Note. An analogous interpretation may be
extended to any zeta-ic function whatever" (OED2).
to denote that the product of factors to
which it is prefixed is to be effected after a certain symbolical
manner. This I shall distinguish as the zeta-ic product. ... Rule for
zeta-ic multiplication. Note. An analogous interpretation may be
extended to any zeta-ic function whatever" (OED2).