Earliest Known Uses of Some of the Words of Mathematics (A)
Last revision: June 24, 2017
ABBE-HELMERT CRITERION for randomness is named for Ernst Abbe and F. R. Helmert. The
criterion is based on the first-order serial correlation coefficient
and, according to H. O. A. Wold & L. Juréen Demand
Analysis: A Study in Econometrics p. 332 , “was first proposed
by Abbe (1863) and a large-sample theory was developed by Helmert
(1905).” The articles referred to are Abbe (1863),
“Über die Gesetzmässigkeit in der Vertheilung der Fehler
bei Beobachtungsreihen” in Gesammelte Abhandlungen,
2, 55 – 81. and Helmert (1905) “Über die
Genauigkeit der Kriterien des Zufalls bei Beobachtungsreihen,”
Sitzungsberichte der Kgl. Preussischen Akad. der Wissenschaften
1905, 594-512. Abbe’s work is particularly remarkable, coming so
many years before the era of modern time series analysis. Compare the
entries SERIAL CORRELATION and CORRELOGRAM.
ABELIAN EQUATION is named for a kind of equation treated by
Niels Henrik Abel
(1802-1829) in his "Mémoire sur une classe particulière
d'équations résoluble algébriquement" (1829)
Oeuvres Complètes, 1, 478-514.
Leopold Kronecker
(1823-1891) introduced the term Abelsche Gleichung in an
1853 paper on algebraically soluble equations, "Über die algebraisch auflösbren
Gleichungen, erste Abhandlung" in
Werke
IV, p. 27ff. Kronecker used the term to describe an equation which in modern
terms would be described as having cyclic Galois group. According to B. L. van
der Waerden A History of Algebra (1985, p. 149) Kronecker was the first
German mathematician to fully recognise the importance of the investigations
of Abel and Galois on the solubility of algebraic equations.
Abelian equation is found in English in 1861 in Rep. Brit. Assoc. Advancem. Sci. 1860: “As we can always express the roots
of an Abelian equation by radicals.., so also the solution of an Abelian congruence depends ultimately on the solution of binomial congruences.”
[John Aldrich, Peter M. Neumann, OED]
ABELIAN FUNCTION. C. G. J. Jacobi (1804-1851) proposed the term Abelsche
Transcendenten (Abelian transcendental functions) in Crelle's Journal 8 (1832)
Werke
III, p. 481. (DSB).
Abelian (function) is found in English in 1846 in Examples
of the Processes of the Differential and Integral Calculus (ed. 2)
ii by D. F. Gregory: “There are also many memoirs in
Crelle’s Journal, both on elliptic functions, and on those which
are called hyper-elliptic or Abelian.” [OED]
Abelian function appears in the title "Zur Theorie der Abelschen
Functionen" by Karl Weierstrass (1815-1897) in Crelle's Journal, 47 (1854) reprinted in
Werke
I, p. 132.
Weierstrass' first publications on Abelian functions appeared in the
Braunsberg school prospectus (1848-1849) reprinted in
Werke
I, p. 111.
ABELIAN GROUP. Camille Jordan (1838-1922) wrote groupe abélien in 1870 in
Traité
des Substitutions et des Equations Algébraiques. However, Jordan does
not mean a commutative group as we do now, but instead means the symplectic
group over a finite field (that is to say, the group of those linear transformations
of a vector space that preserve a non-singular alternating bilinear form). In
fact, Jordan uses both the terms "groupe abélien" and "équation
abélienne." The former means the symplectic group; the latter is a natural
modification of Kronecker's terminology and means an equation of which (in modern
terms) the Galois group is commutative.
An early use of “Abelian” to refer to commutative groups is H. Weber,
“Beweis des Satzes, dass jede eigentlich primitive quadratische Form
unendlich viele Primzahlen darzustellen fähig ist,”
Mathematische
Annalen, 20 (1882), 301--329. The term is used in the first
paragraph of the paper without definition; it is given an explicit definition
in the middle of p. 304.
Abelian group is found in English in 1892 in F. N. Cole tr. E. Netto Theory Substitutions Contents:
“Groups analogous to the Abelian groups.”
[Peter M. Neumann, Julia Tompson, OED]
The term ABELIAN INTEGRAL is found in a letter of Sept. 8, 1844, from William Henry Fox Talbot:
"What is the definition of an Abelian Integral? for it appears to me that
most integrals possess the Abelian property."
The letter was addressed to John Frederick William Herschel, who, in his reply of Sept. 13, 1844, wrote:
"I suppose the most general definition of an Abelian Integral might be
taken to be this that between +(x) and +(φ(x)) there shall subsist an
algebraical relation between several such functions."
[The Talbot letters are available at
http://foxtalbot.dmu.ac.uk/.]
The term ABELIAN THEOREM was introduced by C. G. J. Jacobi
(1804-1851). He proposed the term in Crelle's Journal 8
(1832), writing that it would be "very appropriate" (DSB).
ABSCISSA. According to Cajori (1919, page 175), “The
words ‘abscissa’ and ‘ordinate’ were not used by
Descartes. ... The technical use of ‘abscissa’ is observed
in the eighteenth century by C. Wolf and others. In the more general
sense of a ‘distance’ it was used earlier by B. Cavalieri in
his Indivisibles, by Stefano degli Angeli (1623-1697), a professor of
mathematics in Rome, and by others.”
Abscissa is found in Latin in 1656 in
Exercitationum Mathematicarum
by Frans van Schooten. See page 285.
[Bill Stockich]
According to Cajori (1906, page 185), “The term abscissa
occurs for the first time in a Latin work of 1659, written by Stefano
degli Angeli (1623-1697), a professor of mathematics in Rome.” A
footnote attributes this information to Moritz Cantor.
Abscissa was used in Latin by Gottfried Wilhelm Leibniz
(1646-1716) in “De linea ex lineis numero infinitis ordinatim
ductis inter se concurrentibus formata....,” Acta Eruditorum
11 1692, 168-171 (Leibniz, Mathematische Schriften, Abth. 2,
Band I (1858), 266-269).
According to Struik (page 272), “This term, which was not new
in Leibniz's day, was made by him into a standard term, as were so many
other technical terms.”
For the word in English the OED cites a passage from 1706: H.
Ditton An Institution of Fluxions p. 31 “’Tis
required to find the relation of the Fluxion of the Ordinate to the
Fluxion of the Abscisse.”
See the entry ORDINATE.
ABSOLUTE CONTINUITY. The concept was introduced in 1884 by E. Harnack
“Die allgemeinen Sätze über den Zusammenhang der Functionen
einer reellen Variabelen mit ihren Ableitungen. II. Theil.”
Math.
Ann. 21, (1884), 217-252. The term was introduced in 1905 by G. Vitali.
In the meantime several mathematicians had used the concept. See T. Hawkins Lebesgue’s
Theory of Integration.
ABSOLUTE CONVERGENCE was defined by Cauchy (DSB).
Absolute convergence and unconditional convergence
appear in 1893 in A Treatise on the Theory of Functions by
James Harkness and Frank Morley: "A series is said to converge
absolutely when it still converges after all negative signs
have been changed to positive. ... A convergent series which is
subject to the commutative law is said to be unconditionally
convergent; otherwise it is said to be conditionally
convergent. ... Absolute convergence implies unconditional
convergence."
ABSOLUTE DIFFERENTIAL CALCULUS or il calcolo differenziale assoluto was the name given by the Italian geometer
Gregorio
Ricci-Curbastro to a form of differential calulus he developed that is
independent of the coordinate system. The subject is now usually called TENSOR ANALYSIS.
ABSOLUTE VALUE. In his Disquisitiones arithmeticae (1801), Gauss used
magnitudo absoluta (article 361, page 454).
An 1807 French translation of Euler’s Elements of Algebra uses valeur absolue. An English translation of the French is:
“We have supposed that the numbers p and q
must both be positive; of course if one makes them both negative, it
does not make any change in the absolute value of the proposed formula;
it does not make any change of sign in the case where the exponent is
odd; and it is absolutely the same in the case where the exponent is
even; thus it is not important which signs on gives to the numbers p and q, as long as we suppose both are of the same sign.”
Absolute value is found in English in 1816 in a translation of
An elementary treatise on the differential and integral calculus by Lacroix. [OED]
Searches at Google print give absolute Werth in 1831 and 1844, absolute Grösse in 1836, 1841, and 1853,
and absolute länge in 1853.
Absolute Betrag is found in 1851 in Die Reihenentwickelungen der Differenzial- und Integralrechnung by
Dr. Oskar Schlömilch. This is a use in the modern sense.
Cayley used the term absolute magnitude in 1856, Coll. Works. Vol II page 359:
“...it follows that x will be in absolute magnitude greater or less than 1, i.e., the points in question
will be imaginary or real, according as a > 1 or a < 1.”
The Century Dictionary (1889-1897) has absolute magnitude, rather
than absolute value.
James A. Landau, Wilfried Neumaier, and Julio González Cabillón contributed to this entry.
See also MODULUS and the entry on the Earliest Uses of Function
Symbols.
ABSTRACT ALGEBRA is found in 1860 in
The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science:
“It is the essential principle of abstract algebra to furnish rules and symbols of operation
which are proper for calculating independently of the knowledge of relative magnitudes.” [OED]
ABUNDANT NUMBER. Theon of Smyrna (about A. D. 130)
distinguished between perfect, abundant, and deficient numbers.
A translation of Chapter XIV of Book I of Nicomachus has:
Now the superabundant number is one which has, over and
above the factors which belong to it and fall to its share, others in
addition, just as if an animal should be created with too many parts
or limbs, with 10 tongues as the poet says, and 10 mouths, or with 9
lips, or 3 rows of teeth, or 100 hands, or too many fingers on one
hand. Similarly, if when all the factors in a number are examined
and added together in one sum, it proves upon investigation that the
number's own factors exceed the number itself, this is called a
superabundant number, for it oversteps the symmetry which exists
between the perfect and its own parts. Such are 12, 24, and certain
others, . . .
This citation was provided by Sam Kutler.
Abundaunt number is found in English in 1557 in Whetstone
of Witte by Robert Recorde: "Imperfecte nombers be suche, whose
partes added together, doe make either more or lesse, then the whole
nomber it self... And if the partes make more then the whole nomber,
then is that nomber called superfluouse, or abundaunt" (OED2).
ACUTE ANGLE. See the entry RIGHT, OBTUSE and ACUTE ANGLES.
ACUTE TRIANGLE. Oxygon appears in its Latin form in
1570 in Sir Henry Billingsley's translation of Euclid: "An oxigonium
or an acuteangled triangle, is a triangle which hath all his three
angles acute" (OED2).
Acutangle triangle appears in 1685 in R. Williams,
Euclid: "Oxygone, or Acutangle triangle is that whose angles
are all acute" (OED2).
Oxygon is found in 1838 in Sir William Rowan Hamilton,
Logic,: "Oxygon, i.e. triangle which has its three angles
acute" (OED2).
Acutangular appears in Chambers Cyclopaedia in 1727-41:
"If all the angles be acute..the triangle is said to be acutangular,
or oxygonous" (OED2).
ADDEND. Johann Scheubel (1494-1570) in an arithmetic
published in 1545 wrote numeri addendi (numbers to be
added).
Orontius Fineus (1530) used addendi alone (1555 ed., fol. 3),
according to Smith (vol. 2, page 89).
Addend was used in English by Samuel Jeake (1623-1690), in
Logisicelogia, or arithmetic surveighed and reviewed, written
in 1674 but first published in 1696:
"Place the Addends in rank and file one directly under another" (OED2).
ADDITION. Fibonacci used the Latin additio,
although he also used compositio and collectio
for this operation (Smith vol. 2, page 89).
The word is found in English in about 1300 in the following passage:
Here tells (th)at (th)er ben .7. spices or partes of
(th)is craft. The first is called addicion, (th)e secunde is called
subtraccion. The thyrd is called duplacion. The 4. is called
dimydicion. The 5. is called multiplicacion. The 6. is called
diuision. The 7. is called extraccion of (th)e rote.
In the above, (th) is a thorn. The citation is from "The crafte of
nombrynge" (ca. 1300), one of the earliest manuscripts [Egerton ms.
2622] in the English language that refers to mathematics. The
transcription was carried out by Robert Steele (1860-1944), and it was
first privately printed in 1894 by the Early English Text
Society (London). It was later included in "The Earliest
arithmetics in English," a sourcebook edited by Robert Steele, and
published for the same Society, by H. Milford, Oxford University
Press, xviii, 84 pages, London, 1922. [Julio González
Cabillón]
ADDITIVE IDENTITY is found in 1953 in First Course in
Abstract Algebra by Richard E. Johnson [James A. Landau].
ADDITIVE INVERSE is found in the 1953 edition of A Survey
of Modern Algebra by Garrett Birkhoff and Saunders MacLane. It
may be in the first edition of 1941 [John Harper]. It is also found
in 1953 in First Course in Abstract Algebra by Richard E.
Johnson [James A. Landau].
ADDITIVITY (in ANOVA) is found
in 1947 in C. Eisenhart, "The Assumptions Underlying the Analysis of Variance,"
Biometrics, 3, 1-21 (David, 1995).
See VARIANCE.
ADEQUALITY. The Latin word adaequalitas was used by Pierre de Fermat.
André Weil writes in Number Theory, An approach through history from Hammurapi to Legendre:
“[Fermat] introduces the technical term adaequalitas,
adaequare, etc., which he says he has borrowed from Diophantus. As
Diophantus V.11 shows, it means an approximate equality, and this is
indeed how Fermat explains the word in one of his later writings.”
According Mikhail Katz, Diophantus coined the term parisotes to refer to
an approximate equality. The term was rendered as adaequalitas in
Claude Gaspard Bachet de Méziriac’s Latin translation of Diophantus, and
adéquation and adégaler in Paul Tannery's French translation of Fermat’s
Latin treatises on maxima and minima and related problems.
[Information from the Wikipedia article Adequality.]
ADJOINT EQUATION. Lagrange used the term équation
adjointe.
In 1889, T. Craig wrote in Treat. Linear Differential Equations:
When Chapter I was written..I had not seen Forsyth's
memoir, and had not been able to find an adopted English term for
Lagrange's équation adjointé, so I used the word
adjunct, suggested by the German adjungirte, and not
unlike the French adjointe. It seems better now, however, to
employ the word associate, or, when speaking simply of
Lagrange's équation adjointé, the word
adjoint.
This citation was taken from the OED2.
ADJOINT LINEAR FORM appears in 1856 in Arthur Cayley,
"A Third Memoir Upon Quantics," Philosophical Transactions of the Royal Society
of London Vol. 146. (1856), pp. 627-647 reprinted in
Papers
II p. 310 [University of Michigan Historical Math Collection].
ADJOINT MATRIX. The OED quotes from M. Bôcher's Introduction to Higher Algebra of 1907:
"By the adjoint A of a matrix a is understood another matrix of the same order in which
the element in the ith row and jth column is the cofactor of the element in the jth row and
ith column of a." (p. 77)
ADMISSIBLE ESTIMATE and admissible system
of (acceptance) regions appear in Wald's 1939 "Contributions to the Theory
of Statistical Estimation and Testing Hypotheses," Annals of Mathematical
Statistics, 10, 299-326 [John Aldrich, based on David (2001)].
See DECISION THEORY.
AFFINE. Affinis and affinitas were first used by Leonhard
Euler in Introductio in analysin infinitorum (1748) Chapter XVIII: "De
similitudine et affinitate linearum curvarum." He also wrote (II. xviii.
239): "Quia Curvae hoc modo ortae inter se quandam Affinitatem tenent,
has Curvas affines vocabimus."
The words continued to be used a little throughout the 19th century, for example
in Möbius "Der barycentrische Calcul" (1827) Chapter 3: "Von
der Affinitaet." There is a brief historical summary of this stage by E.
Papperitz in the Encyclopaedie
der mathematische Wissenschaften III A B 6 (1909), p.517. [Ken Pledger]
Affine is found in English in 1895 in Annals of
Mathematics: “Let us find the differential equations of the
first order which are invariant under the G1 of the affine
transformations in the plane.” [OED]
ALGEBRA comes from a phrase in the title of a work written in Arabic around 825 by
al-Khowarizmi,
al-jabr w'al-muqâbalah.
Wikipedia.
Katz explains the use of the terms: al-jabr refers to the operation of transposing a subtracted quantity on one side of an
equation to the other side where it becomes an added quantity; al-muqâbalah refers to the reduction of a
positive term by subtracting equal amounts from both sides of the equation.
The word al-jabr means “the reunion
of broken parts” and when the Moors took the word al-jabr into Spain, an algebrista being a restorer,
one who resets broken bones. Thus in Don Quixote (II, chap. 15), mention is
made of “un algebrista who
attended to the luckless Samson.” At one time it was not unusual to see
over the entrance to a barber shop the words “Algebrista y Sangrador”
(bonesetter and bloodletter) (Smith vol. 2, pages 389-90). The word in this
sense also had some currency in English. Thus the OED has a quotation from a book on surgery from 1541:
“The helpes of Algebra & of dislocations.”
Returning to mathematics, when the work of al-Khowarizmi was translated into Latin—around
1140 by Robert of Chester—the words in the title were not translated, instead
the Arabic words were borrowed. Thus the title became Liber algebrae et almucabala. Viète disliked
the word algebra because it had no meaning in any European language and promoted instead the term analytic art:
see the entry ANALYSIS. The original Arabic/Latin phrase is echoed in English in John Dee’s
Preface to Billingsley’s translation (1570) of Euclid’s Elements:
“The Science of workyng Algiebar and Almachabel, that is, the Science of findyng an
vnknowen number, by Addyng of a Number, and Diuision and æquation.” In the text
Billingsley drops the second half of the original phrase and uses the first
half in a more general way: “That more secret and subtill part of Arithmetike,
commonly called Algebra.” Robert Recorde had done the
same a few years before in The Pathwaie to Knowledge in 1551: “Also the rule of false position, with dyvers examples not
onely vulgar, but some appertayning to the rule of Algeber.” These quotations are from the OED.
It was once believed that the word algebra was derived from the name Gabir ben Allah of Sevilla, commonly called Geber, a
celebrated astronomer apparently skilled in algebra. Joseph Raphson's Mathematical Dictionary (1702) has:
“Algebra, from Al in Arabick which signifies Excellent, and Geber the Name of the supposed Inventor of
it....” This etymology based on EPONYMY is
not totally absurd: compare the word ALGORITHM.
The algebra of al-Khowarizmi was the
name for an operation used in solving an equation but by 1600 the word was
applied to the study in which that operation was used. The word continued to be
applied to a study, but one whose scope increased enormously especially in the
19th and 20th centuries. See the Historical Survey in the
Encyclopaedia of Mathematics and the entries
GROUP, FIELD, MATRIX, RING, VECTOR SPACE and other algebra topics.
In the 19th and 20th centuries the word algebra acquired further meanings. It is
sometimes used to mean a formal calculus as in the title of Schröder’s book of
1890 Vorlesungen über die Algebra der Logik.
An early expression of this point of view is found in Augustus de Morgan’s
Trigonometry
and Double Algebra (1849, p. 101):
“It is most important that the student should bear in mind that, with one exception, no word nor sign of
arithmetic or algebra has one atom of meaning throughout this chapter, the
object of which is symbols, and their laws of combination, giving a symbolic
algebra (page 92) which may hereafter become the grammar of a
hundred distinct significant algebras.”
The term is also used in some very specific constructions, e.g. Boolean algebra and algebra of sets (in measure theory).
A JSTOR search found Boolean algebra in
the title of a 1913 article by Sheffer while the expression algebra of sets (an abbreviation for Boolean algebra of sets) was popularised
by Halmos’s Measure Theory (1950). See the Encyclopaedia of Mathematics entries
Boolean algebra and
Algebra of sets.
ALGEBRAIC CURVE. See TRANSCENDENTAL CURVE.
ALGEBRAIC FUNCTION is found in English in 1794
in An Essay on the Principles of Human Knowledge by E. Waring, M. D.:
"8. Infinite series: e. g. let a quantity denoting the ordinate, be an algebraic function
of the abscissa x, by the common methods of division and extraction of roots, reduce it
into an infinite series ascending or descending according to the dimensions of x, and then
find the integral of each of the resdulting terms." [Google print search]
ALGEBRAIC GEOMETRY is found in 1821 in Cambridge Problems. [OED]
ALGEBRAIC LOGIC. The following is from "From Paraconsistent Logic to
Universal Logic" by Jean-Yves Béziau:
The road leading from the algebra of logic to algebraic logic is an interesting object of study for the
historian of modern logic which has yet to be fully examined. Curry stands in the middle of the road, he
was the first to use the expression "algebraic logic" in (Curry 1952) and not Halmos as erroneously stated
in (Blok/Pigozzi 1991, p. 365), but what he meant by it was still close to algebra of logic. Halmos
introduced this expression rather to denote the algebraic treatement of first-order logic, but nowadays the
expression "algebraic logic" is used to include both the zero and the first-order levels.
ALGEBRAIC NUMBER. According to an Internet web page, this term
was used by Abel.
Algebraic quantity appears in 1673 in Elements of Algebra
(1725) by John Kersey: "Two or more Algebraic quantities" (OED2).
Algebraic (in the sense of an algebraic number) is found in
1840 in Mathematical Dissertations (1841) by J. R. Young
[James A. Landau].
Algebraic number appears in 1870 in the title "Kritische Untersuchungen
über die Theorie der algebraischen Zahlen" by H. Schwarz.
ALGEBRAIC TOPOLOGY appears in 1942 in the title Algebraic Topology
by Solomon Lefschetz. A JSTOR search found a slightly earlier appearance in Norman E. Steenrod “Universal
Homology Groups,” American Journal of Mathematics, 58, (1936), 661-701.
ALGORITHM is derived via Latin from the Arabic al-Khowarazmi, the native of Khwarazm
(Khiva), surname of the Arab mathematician and astronomer
Abu
Ja'far Mohammed Ben Musa (c. 780 - c.850).
The OED has separate entries for algorithm and the earlier algorism. It
says that algorithm is derived from
the earlier word algorism and "influenced by the Greek word arithmos
(number)." However, other dictionaries show algorism as a Middle English spelling of algorithm.
The term originally meant "arithmetic" or "the Hindu-Arabic numerals."
In the twelfth century, the arithmetic of al-Khowarazmi
was translated into Latin by Robert of Chester and it bore the name Algoritmi
de numero indorum meaning al-Khowarazmi on the Hindu numbers.
In Middle English augrim, algorisme, and other spellings are found. Chaucer used augrym.
Recorde used augrim and algorisme.
In 1503 in Margarita philosophica Gregor Reisch used the headings Algorithmus de minutijs vulgaribus,
Algorithmus de minutijs physicalibus, and
Algorithmus cum denarijs piectilibus: seu calcularis.
Under these headings are rules for handling fractions, astronomical fractions,
and rules for computing on the reckoning board.
Algorithmus appears in 1534 in Algorithmus demonstratus by Johann Schoner.
Algorithmus (in the sense of a systematic technique for solving a problem) was
used by Gottfried Wilhelm Leibniz in 1684:
Ex cognito hoc velut Algorithmo, ut ita dicam,
calculi hujus, quem voco differentialem, omnes aliae
aequationes differentiales inveniri possunt per calculum communem,
maximae que & minimae, item que tangentes haberi, ita ut opus non sit
tolli fractas aut irrationales, aut alia vincula, quod tamen faciendum
fuit secundum Methodos hactenus editas. (From this rule, known as an
algorithm, so to speak, of this calculus, which I call differential,
all other differential equations may be found by means of a general
calculus, and maxima and minima, as well as tangents [may be]
obtained, so that there may be no need of removing fractions, nor
irrationals, nor other aggregates, which nevertheless formerly had to
be done in accordance with the methods published up to the present.)
The citation above is from "Nova Methodvs pro maximis et minimis,
itemque tangentibus, quae nec fractas, nec irrationales quantitates
moratur, & singulare pro illis calculi genus, per G.G.L." (A new
method for maxima and minima, as well as tangents, which is not
obstructed by fractional or irrational quantities), Leibniz' first
published account of the calculus [Acta Eruditorum, vol. 3,
pp. 467-473, October 1684], page 469. Both terms "Algorithmo" and
"differentialem" are italicized in the original. The English
translation is from Evelyn Walker's translation of extracts from
Leibniz' memoir found on p. 623 of Smith's Source Book in
Mathematics (1929), vol. 2.
Algorithm is found in English in 1699 in
Phil. Trans. XXI. 263: "The Algorithm or Numeral Figures now in use" (OED2).
Algorithm is found in English in 1715 in The Theory of Fluxions
by Joseph Raphson: "Now from this being known as the
Algorithm, as I may say of this Calculus, which I call differential,
..." (p.23).
Algorithm was used by Euler, for instance in
his article "De usu novi algorithmi in problemate Pelliano solvendo,"
and its use was then firmly established.
According to the Theseus Logic, Inc., website, "The term algorithm
was not, apparently, a commonly used mathematical term in America or
Europe before Markov, a Russian, introduced it. None of the other
investigators, Herbrand and Godel, Post, Turing or Church used the
term. The term however caught on very quickly in the computing
community."
[Julio González Cabillón, Heinz Lueneburg, David Fowler, and John Aldrich contributed to this entry.]
ALIAS as a term in the theory of experimental design appears in D. J. Finney's
"The Fractional Replication of Factorial Arrangements," Annals
of Eugenics, 12, (1945), 291-301. (David (2001))
ALIQUOT PART. Aliqi is an adjective in Latin meaning
"some" or "any."
St. Augustine of Hippo (354-430) wrote in De Civitate Dei:
"Itemque in denario quaternarius est aliqua pars eius..."
Aliquot part occurs in English in 1570 in Sir Henry
Billingsley's translation of Euclid's Elements: "This..is
called .. a measuring part .. and of the barbarous it is called ..
an aliquote part" (OED2).
The term ALLOTRIOUS FACTOR was coined by James Joseph
Sylvester.
The term ALMOST PRIME OF ORDER r was "apparently
introduced" by B. V. Levin in "A one-dimensional sieve," (Russian)
Acta Arith. 10 (1964/65), 387-397. MR 31, 4774, according to
H. Halberstam and H.-E. Richert in Sieve Methods (1974) [Paul
Pollack].
The term ALPHAMETIC was coined in 1955 by J. A. H. Hunter
(Schwartzman). In the Dec. 23, 1955, Toronto Globe & Mail
Hunter wrote, "These alphametics seem set to take the place of
crosswords as a new craze... Don't forget that each letter stands for
a particular figure" (OED2).
ALTERNATE ANGLE. Henry Billingsley’s
1570 translation of Euclid’s Elements has:
“If a right line falling vpon two right lines,
do make the alternate angles equall the one to the other:
those two right lines are parallels the one to the other.” [Alan Hughes]
In 1828, Elements of Geometry and Trigonometry (1832) by
David Brewster (a translation of Legendre) has:
AGO, GOC, we have already named interior angles on the
same side; BGO, GOD, have the same name; AGO, GOD, are called
alternate interior angles, or simply alternate; so
also, are BGO, GOC: and lastly EGB, GOD, or EGA, GOC, are called,
respectively, the opposite exterior and interior angles; and
EGB, COF, or AGE, DOF, the alternate exterior
angles.
In May 1940, a review in The Mathematics Teacher has: “While
the writer is correct in saying that the abbreviated description is
in general use for ‘the exterior angles on the same side of the
transversal,’ he is wrong about the ‘interior angles on the same side
of the transversal.’ At least two textbooks use the satisfactory
description ‘consecutive interior angles’ as a substitute for the
latter clumsy expression. The reference to the exterior angles on the
same side of the transversal is so infrequent as not to warrant a
need for an abbreviated description.”
ALTERNATING GROUP appears in Camille Jordan, "Sur la limite de
transitivité des groupes non alternés," Bull. Soc.
math. de France 1 (1873).
Alternating group is found in English in 1886 in
American Journal of Mathemtaics 8/275: “The Borchardt
moduli...are irrational to a considerable degree, and their group is 32-1-edric isomorphic
with the alternating group of the x’s.” [OED]
ALTERNATING SERIES is found in 1817 in Philosophy of Arithmetic by Sir John
Leslie: “The original fraction...is converted by substitution into the alternating series, [etc.].”
[OED]
ALTERNATIVE HYPOTHESIS. See HYPOTHESIS and HYPOTHESIS TESTING.
AMBIGUOUS CASE. In 1761 Navigation New Modelled
by Henry Wilson has "...where the Case is so ambiguous by Sol. 8..."
[Google print search]
Ambiguous case is found in 1827
in Mathematical and astronomical tables by William Galbraith:
"If in this triangle the side B be greater than C, there may be two triangles
formed, constituting what is called the ambiguous case, that is, it admits
of two solutions, either of which answers the conditions required, unless
from some known circumstances one of htem must be adopted in preference to the other."
[Google print search]
AMENABLE semigroups.
In his “Amenable semigroups,” Illinois Journal of Mathematics, 1, 509-544 M. M. Day gives the definition,
“A semigroup Σ is called
amenable if there is a mean μ on m(Σ) which is both left and right invariant.” A good pun
needs no explanation and so Day does not point out that the term fuses
“amenable” in its usual meaning with the barbarism “meanable.” Day’s term was
an improvement on “messbar” (measurable) used in J. von Neumann (1929) Zur
allgemeinen Theorie des Maßes, Fundamenta
Mathematicae, 13,
73-116. Day reflected on the success of the paper and its
title in This
week’s citation classic June 27 1983.
In a 2010 email, Peter Flor writes:
The English word amenable was intended by M. Day, who introduced the term, to remind the audience of the word "mean" since the concept of amenability is defined by the existence of a certain mean. Now, "mean" (in the mathematical sense) is "Mittel" in German, and "moyenne" in French. Accordingly, amenable (semi-)groups were called "mittelbar" in German and "moyennable" in French, since about 1950. J.-P. Pier, author of the book Amenable Locally Compact Groups, called them "groupes moyennables" in his earlier publications in French. The German word "mittelbar" might be called a barbarism, just like your characterization of the non-existing word "meanable" which may have induced Day to coin the term "amenable". However, "mittelbar" is certainly more suitable than von Neumann’s "messbar" which usually means measurable.
See also Wikipedia amenable group.
AMICABLE NUMBERS. The philosopher Iamblichus of Chalcis (c. 250-330)
wrote that the Pythagoreans called certain numbers amicable numbers. An Internet
web page claims Pythagoras coined the term.
Ibn Khaldun (1332-1406) used a term which is translated "amicable (or
sympathetic) numbers."
In his 1796 mathematical dictionary, Hutton says he believes the term amicable
number was coined by Frans van Schooten (1615-1660).
The term appears in the title De numeris amicabilibus by Euler (1747)
in Opera
mathematica. Series prima. Volumen II p. 59.
Sometimes the terms amiable or agreeable are used.
AMPLITUDE (of an elliptic integral, meaning the angle subtended by
the elliptical arc) appears in French (same spelling as in English) in 1786 in Legendre’s
paper Second Mémoire sur les Intégrations par arcs d’ellipses, which was
published in the Histoire de l’Académie royale des sciences, Année
MDCCLXXXVI avec les mémoires de Mathématique & de Physique. [James A. Landau]
The term ANALLAGMATIC was used by James Joseph Sylvester
(1814-1897) (Schwartzman).
The OED2 has an 1869 citation, Clifford, Brit. Assoc. Rep. 8:
"On the Umbilici of Anallagmatic Surfaces."
ANALYSIS is a term with a long history in Mathematics and its meaning has changed several times. The
word comes via Medieval Latin from the Greek, 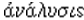 derived from the verb
derived from the verb 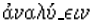 to unloose, undo. T. Heath writes in A History of Greek Mathematics, volume 1 (1921, p. 291), “analysis [was] according to the ancient view nothing more
than a series of successive reductions of a theorem or a problem till it is
finally reduced to a theorem or problem already known.” Kline (page 279)
states that the term was introduced by
Theon of Alexandria.
to unloose, undo. T. Heath writes in A History of Greek Mathematics, volume 1 (1921, p. 291), “analysis [was] according to the ancient view nothing more
than a series of successive reductions of a theorem or a problem till it is
finally reduced to a theorem or problem already known.” Kline (page 279)
states that the term was introduced by
Theon of Alexandria.
François Viète
used the term analytic art for algebra in 1591 in In artem analyticem
isagoge. Schwartzman (page 23) says that “the French
mathematician Viète opted for the term analysis rather than algebra, claiming
that algebra doesn’t mean
anything in any European language. He didn't succeed in driving out the word algebra, but he did popularize analysis to the point where it has stayed
with us.” See the entry ALGEBRA.
The earliest quotations in the OED illustrate this
sense of analysis as algebra: "Simple Analysis is that
employed in solving problems reducible to simple equations" (Chambers's Cyclopedia
Supplement of 1753); "Analysis or the Analytic Method .. is
that which is commonly used in Algebra" (Charles Hutton A Course of Mathematics of 1827).
In The Purloined Letter
(1845), Edgar Allan Poe wrote:
The mathematicians, I grant you, have done their best to promulgate
the popular error to which you allude, and which is none the less an error for
its promulgation as truth. With an art worthy a better cause, for example, they
have insinuated the term 'analysis' into application to algebra. The French
are the originators of this particular deception; but if a term is of any importance
-- if words derive any value from applicability -- then 'analysis' conveys
'algebra' about as much as, in Latin, 'ambitus' implies 'ambition', 'religio'
'religion', or 'homines honesti', a set of honorable men."
Poe was out of date for the French were again redefining analysis.
Perhaps Lagrange had set the scene for analysis to invade calculus with his
project to found calculus on algebra; see his lectures
Théorie des
fonctions analytiques contenant les principes du calcul différentiel dégagés
de toute considération d'infiniment petits et d'évanouissans, de limites ou
de fluxions et réduits à l'analyse algébrique des quantités finies
(1797). Beginning with Cauchy's Cours d'analyse de l'École Royale Polytechnique of 1821
(Oeuvres II.3),
Cours d'analyse was the title French authors chose for their advanced works on calculus.
Analysis with its modern meaning in English is found in
1802 in a review of J. E. Montucla, “A History
of Mathematics,” in The Critical Review; or, Annals of Literature; Extended & Improved:
“Several new branches of analysis having arisen out of the foregoing, the author treats of them to such extent
as the nature of his work will permit; such as the calculus of finite differences; that of circular, logarithmic,
and imaginary quantities; the methods of limits, of analytic functions, of variations, of partial differentials,
of infinite series, of eliminations, of interpolations, of continued fractions, &c.” [Google print search,
James A. Landau]
In the later 20th century the scope of analysis increased as newcomers such as
FUNCTIONAL ANALYSIS were accommodated. Numerous sub-fields are now
distinguished--REAL ANALYSIS, COMPLEX
ANALYSIS, classical analysis, modern analysis etc.
For a list of entries associated with
analysis see here.
[John Aldrich contributed to this entry.]
The term ANALYSIS OF ALGORITHMS was coined by Donald E. Knuth.
The term appears in the preface to his The Art of Computer
Programming, Volume 1 [Tim Nikkel].
ANALYSIS OF VARIANCE. See VARIANCE.
ANALYSIS SITUS. See TOPOLOGY.
ANALYTIC ARITHMETIC. At the end of the sixteenth century, a few
authors, following Viete's interest in analysis, attached the word
"analytic" to some terms related to math. For instance, Nicholas
Reimers Ursus (1551-1600) used the expression arithmetica
analytica in Nicol. Raimari arithmetica analytica vulgo Cosa,
oder Algebra, published posthumously in 1601. [Julio
González Cabillón]
The term ANALYTIC EQUATION was used by Robveral in De
geometrica planarum & cubicarum aequationum, printed posthumously
in 1693: "Dicitur locus aliquis geometricus ad aequationem
analyticam revocari, cum ex una aliqua, vel ex pluribus ex illlius
proprietatibus specificis, quaedam deducitur aequatio analytica, in
qua una vel duae vel tres ad summum sint magnitudines incognitae."
[Barnabas Hughes]
In modern analysis the term ANALYTIC FUNCTION is used
in two ways: (of a complex function) having a complex derivative at every point
of its domain, and in consequence possessing derivatives of all orders and
agreeing with its Taylor series locally; (of a real function) possessing derivatives of all orders and agreeing with its
Taylor series locally. (Borowski & Borwein)
According to Youschkevitch (pages 37-84), the term was first used by
Marquis
de Condorcet (1743-1794) in his unpublished Traité du Calcul Integral and then more conspicuously by
Joseph
Louis Lagrange (1736-1813) in his
Théorie
des Fonctions Analytiques (1797). For these authors an analytic
function simply signified a function of the kind treated in analysis. [Giovanni Ferraro].
The connection between the usage of Lagrange and modern usage is explained by Judith V. Grabiner in her
The Origins of Cauchy’s Rigorous Calculus: "For Lagrange, all the applications
of calculus ... rested on those properties of functions which could be
learned by studying their Taylor series developments ... Once the question
of convergence has been dealt with, in fact a great deal of information can be
obtained about functions by studying their Taylor-series expansions.
Weierstrass
later exploited this idea in his theory of functions of a complex variable,
retaining Lagrange’s term "analytic function" to designate, for Weierstrass, a
function of a complex variable with a convergent Taylor series." (pp. 52 & 194)
See the Encyclopedia article Analytic function. [John Aldrich]
ANALYTIC GEOMETRY. The following appears as a footnote in Descartes’s Mathematical
Thought by Chikara Sasaki:
According to Boyer, the terminology “analytic geometry”
was used probably for the first time
by Michel Rolle in his “De l'evanouissement des quantitez inconnues dans la geometrie analytique,”
Mémoires de l'Académie royale des sciences (Paris), Année 1709 (1709. 9. Aoust),
pp. 419-450. See Carl B. Boyer, History of Analytic Geometry (New York, 1956), p. 155:
“Incidentally, in Rolle’s discussion of this problem,
the term ‘analytic geometry’ appeared in print, perhaps for the first time, in a sense
analogous that of today.” On p. 141 of the same book Boyer
also refers to Newton’s treatise titled “Artis Analyticae Specimina vel Geometria Analytica,”
which was published in Operae quae exstant omnia, Vol. I, pp. 389-518, under the editorship of Samuel Horsley in London in 1779. The title is ascribed not to the author Newton but to a copyist William Jones.
The tract which Horsley edited as Artis analyticae specimina vel Geometria analytica is basically
identical to “De Methodus serierum et fluxionum,” written in Winter 1670-71, in D. T.
Whiteside, ed, The Mathematical Papers of Isaac Newton, Vol. III (1670-1673), (Cambridge, 1969).
Jones copied Newton’s manuscript about 1710. See Whiteside’s Introduction, Op. cit.,
pp. 11-13. See also Whiteside’s “General Introduction,” in The Mathematical Papers
of Isaac Newton, Vol. I (1664-1666), (Cambridge, 1967), pp. xxiii and xxviii, notes (26) and (34).
I am skeptical about Newton’s use of “analytic geometry” in other works as well.
In 1797 Sylvestre François Lacroix (1765-1843) wrote in
Traité du calcul différentiel et du calcul
intégral: “There exists a manner of viewing geometry that
could be called géométrie analytiques, and which
would consist in deducing the properties of extension from the least
possible number of principles, and by truly analytic methods.” This
quote was taken from the DSB. The Compact DSB states that Lacroix
“was first to propose the term analytic geometry.”
In "The work of Nicholas Bourbaki" (Amer. Math. Monthly, 1970,
p. 140), J. A. Dieudonné protested:
It is absolutely intolerable to use analytical geometry
for linear algebra with coordinates, still called analytical geometry
in the elementary books. Analytical geometry in this sense never
existed. There are only people who do linear algebra badly, by
taking coordinates and this they call analytical geometry. Out with
them! Everyone knows that analytical geometry is the theory of
analytical spaces, one of the deepest and most difficult theories of
all mathematics.
[Julio González Cabillón, Carlos César de
Araújo]
ANCILLARY in the theory of
statistical estimation. The term "ancillary statistic" first appears
in R. A. Fisher's 1925
"Theory of Statistical Estimation.,"
Proc. Cambr. Philos. Soc. 22. p. 724, although interest in ancillary
statistics only gathered momentum in the mid-1930s when Fisher returned to the
topic in Two New Properties of Mathematical Likelihood
and other authors started contributing to it [John Aldrich, David
(1995)].
See ESTIMATION.
ANGLE is the subject of Definition
8 of Book 1 of Euclid’s Elements.
The modern English word derives ultimately from the Latin angulus which could mean corner as well as angle.
The OED’s first citation in English for angle in
the geometric sense is from John Trevisa’s translation (1398) of Bartholomaeus Anglicus De
Proprietatibus Rerum: “Of dyuers touchyng of lynes comeþ diuers
anglis. For som angle hatte rectus angulus,
and somme obliquus and reflexus.” Trevisa does not give English
expressions for the three kinds of angle; for these, see
the entry RIGHT, OBTUSE and ACUTE ANGLES.
ANGLE OF DEPRESSION. A Google print search finds angle of depression in 1723 in A System of Mathematics... by
James Hodgson: “From the Parallax of Altitude or Angle of Depression, by the means of
which the Planets appear at a greater distance from the Zenith than otherwise
they would do....” [James A. Landau]
ANGLE OF ELEVATION. A Google print search by James A. Landau finds angle of elevation in a 1686 paper by E. Halley,
“A Discourse Concerning Gravity, and its Properties, wherein the Descent of
Heavy Bodies, and the motion of Projects is briefly, but fully handled:
Together with the Solution of a Problem of great Use in GUNNERY” in the Philosophical Transactions:
Prop. IX. Problem: A Projection being made as you please, having the Distance and Altitude,
or Descent of an Object, through which the Project passes, together with the Angle of Elevation
of the line of Direction; to find the Parameter and Velocity, that is (in Fig. 2.) having
the Angle FGB, GM, and MX.
ANHARMONIC RATIO and ANHARMONIC FUNCTION. Michel Chasles
coined the terms rapport anharmonique and fonction
anharmonique (Smith vol. 2, page 334).
He used the terms in his "Aperçu historique .... des
Méthodes en Géométrie," 1837, p.35. He uses
essentially the same definition as Möbius, but without the
signs, so a harmonic range gives the value +1 rather than -1. Then
he says "Ce rapport étant dit harmonique dans le cas
particulier où il est égal a l'unité, nous
l'appellerons, dans le cas général, rapport ou
fonction anharmonique" [Ken Pledger].
Anharmonic relation
is found in 1843 in
"Demonstration of Pascal's Theorem" by Arthur Cayley in the Cambridge Mathematical Journal, vol. IV:
"The demonstration of Chasles' form of Pascal's Theorem (viz. that the anharmonic relation of the planes 61, 62, 63, 64
is the same with that of 51, 52, 53, 54), is very much simpler; but as it would require some preparatory information with
reference to the analytical definition of the similarity of anharmonic relation, I must defer it to another opportunity"
[University of Michigan Digital Library].
Anharmonic ratio is found in English in in Arthur Cayley, “On the Triple Tangent Planes of Surfaces of the Third Order,”
The Cambridge and Dublin Mathematical Journal, vol. IV (1849), pp. 118-132:
“Which remains unaltered for cyclical
permutations of l, m, n, ie. the anharmonic ratio of x, ξ, x, 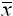 is the same as that of y, η, y,
is the same as that of y, η, y, 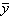 .” [James A. Landau]
.” [James A. Landau]
See also CROSS-RATIO.
ANNULUS. A Google print search finds the phrase annulus nascens (growing ring) in 1739 in an article, “Hydraulicks”
in the Philosophical Transactions, although here it is perhaps not a mathematical term. [James A. Landau]
A Google print search shows that Andrew Motte’s 1803 translation of Newton’s Principia has
“...so as for form a fluid annulus, or ring, of a round figure, and concentrical to the body T; and the several
parts of this annulus, performing their motions by the same law as the body P, will draw nearer to the body T, and move
swifter in the conjunction and opposition of themselves and the body S, than in the quadratures.” [James A. Landau]
Annulus is found in 1834 in the Penny Cyclopedia,
where it is described as “The name of a ring, or solid formed by
the revolution of a circle about a straight line exterior
to its circumference as an axis, and in the plane of the said circle”
(OED2).
ANSATZ. In everyday German
this word has several meanings related to the idea of beginning. Two—at
least—went into German and then into English mathematics. One is found in the
expression Hibert’s Ansatz, an adaptation of der Hilbertische Ansatz which
is found in Hilbert and Bernays Grundlagen der Mathematik (1939) II. p.
21 though the technique is older, going back to Hilbert’s work of the early
1920s. Here Ansatz means formulation or approach.
In mathematical physics ansatz is often used in another
sense, as a “mathematical assumption, especially about the form of an unknown
function, which is made in order to facilitate solution of an equation or other
problem.” (OED). A paper by Hans Bethe is often cited: “Zur
Theorie der Metalle. I. Eigenwerte und Eigenfunktionen der
linearen Atomkette,” Zeitschrift für Physik A, 71, (1931),
205–226. Bethe uses the term Ansatz (see p. 208) without any explanation
which suggests that the usage was already established. In
English E. A. Uehling and G. E. Uhlenbeck wrote the word with an initial
capital letter, as in German, and in quotes to signal the word’s foreign origin:
see “Transport Phenomena in Einstein-Bose and Fermi-Dirac Gases. I,” Physical
Review, 43, (1933), p. 553. Today the word is written like an
ordinary English word. [John Aldrich]
ANTIDERIVATIVE. Anti-derivative appears in 1903 in
"Integration as a Summation" by George R. Dean in
The American Mathematical Monthly.
[JSTOR search] The word may be older.
ANTI-DIFFERENTIAL appears in 1904 in
Elements of the Differential and Integral Calculus
by William Anthony Granville with Percey F. Smith. A footnote to the word integral reads:
"Called anti-differential by some writers" [James A. Landau].
The term ANTILOGARITHM was introduced by John Napier.
It appears in A Description of the Admirable Table of Logarithmes (1616),
an English translation by Edward Wright of Napier's work:
And they are also the Logarithmes of the complements of
the arches and sines towards the right hand, which we call
Antilogarithmes.
APARTMENT, BUILDING, and CHAMBER in group theory. These are
translations of the everyday French words, appartement, immeuble, and chambre. J. Tits writes in “Buildings and
their Applications,” Proceedings of the
International Congress of Mathematicians: Vancouver, 1974 vol. 1, p.
209:
The buildings considered in this talk are particular simplicial complexes naturally
associated to algebraic simple groups. The “real
estate” terminology due to N. Bourbaki [Éléments
de mathématique. Groupes et algèbres de Lie ch. 4-6. 1968], originated in the fact that the maximal
simplexes of these complexes are called “chambers” (in French, “chambre”, that
is, “room”) because of their close connection with the “Weyl chamber” in the
theory of root systems.
In the English translation, N. Bourbaki Lie groups and Lie algebras chapters 4-6 (available on Google books),
the concepts are defined on p. 35. [John Aldrich]
The term APOLAR is due to Th. Reye, according to Maxime
Bôcher in Modern Higher Algebra (1885).
APOTHEM is found in 1822 in Elements of Geoemtry and Trigonometry translated from the French of M. A. Legendre, edited
by David Brewster. [Google print search]
The word does not appear in Euclid or any other ancient Greek text
and appears to be a scholarly neologism [Antreas P. Hatzipolakis].
Apothem is commonly mispronounced; the primary stress is on
the first syllable.
APPLIED MATHEMATICS. See the entry PURE and APPLIED MATHEMATICS.
The term ARBELOS is apparently due to Archimedes. Thomas L.
Heath, in his "The Works of Archimedes" [Cambridge: At the University
Press, 1897], remarks that:
... we have a collection of Lemmas (Liber
Assumptorum) which has reached us through the Arabic. [...] The
Lemmas cannot, however, have been written by Archimedes in their
present form, because his name is quoted in them more than once.
...though it is quite likely that some of the propositions were of
Archimedean origin, e.g. those concerning the geometrical figures
called respectively [arbelos, in Greek] (literally 'shoemaker's
knife') and [salinon, in Greek] (probably a 'salt-cellar'),
...
Arbelos is found in English
in May 1859 in "On Contact, Centres of Similitude, and Radical Axes" by Matthew Collins
in the Mathematical Monthly: "This case is Pappus' Theorem XVI., and was referred to
by him as the Arbelos." [Google print search]
[Ken Pledger, Antreas P. Hatzipolakis, Julio González
Cabillón]
ARBORESCENCE is found in Y.-j. Chu and L. Tseng-hong, On
the shortest arborescence of a directed graph, Sci. Sin. 14,
1396-1400 (1965).
ARBORICITY occurs in G. Chartrand, H. V. Kronk, and C. E.
Wall, The point-arboricity of a graph, Isr. J. Math. 6,
169-175 (1968).
ARCSINE. For early uses of the symbol arc sin (or variations thereof), see the trigonometry page of the companion Math Symbols site.
This entry will show uses of arcsine as a word, spelled with the final e.
A Google print search by James A. Landau finds that “Discussion of Inverse Functions” by Cooper D. Schmitt in American Mathematical Monthly, April 1899, has:
We read it, “x equals the arc whose sine is a, or more briefly, “arc-sine
a,” i. e. x equals arc-sine a. The expression is sometimes read “x
equals the inverse sine of a,” or “the anti-sine of a.”
Arcsine is found in approximately 1904 in the E. R. Hedrick translation of volume I of
A Course in Mathematical Analysis by Edouard Goursat. The translation carries the date 1904, although a footnote
references a work dated 1905. The word appears in running text in the phrase “we obtain the following development
for the arcsine” [James A. Landau].
Arctangent appears in Hedrick (above).
ARGAND DIAGRAM. Jean-Robert
Argand presented his diagram in a small book published in 1806. The book is
reprinted with additional material from 1813-4 in Essai sur une
manière de représenter les quantités imaginaires dans les constructions
géométriques.
A Google print search finds Argand diagram in 1889 in Algebra: An Elementary Text-Book for the Higher Classes of Secondary Schools and
for Colleges by George Chrystal: “If we draw the Argand diagram for w = 1 + x + yi,
we see that when r is given w describes a circle of radius r, whose centre is the point (1, 0).” [James A. Landau]
ARGUMENT. This word derived from the Latin entered English in the 14th century with two basic
meanings, one in logic and one in astronomy. The quotations given in the OED are from the work of
Geoffrey Chaucer who
wrote stories about students of these subjects as well as an unfinished book on
the astrolabe, an instrument used by astronomers; this appears to have been the
earliest technical manual in English.
To illustrate the meaning "a statement or fact advanced for the purpose of influencing the mind"
the OED quotes from Chaucer’s
Franklin’s
Tale line 178 "Clerkes wol seyn as hem leste By Argumentz that
al is for the beste." Related meanings include dispute and process of
reasoning.
To illustrate the meaning "the angle, arc, or other mathematical quantity, from which another
required quantity may be deduced, or on which its calculation depends" the OED
quotes from the Franklin’s
Tale line 549 "Hise othere geeris, As been his centris and hise
Argumentz" and from the Treatise on the Astrolabe.
xliv. 54 "To knowe the mene mote and the argumentis of any planete."
The related meanings here include the argument (or phase or amplitude) of a complex number and the
argument (or INDEPENDENT VARIABLE) of a function.
For the first see Briot & Bouquet’s
Théorie
des fonctions elliptiques (1859, p. 1). Today argument is the most popular English term
but a century ago there were several alternatives: "We find [the angle]
designated as argument, declination, arcus, anomalie, amplitude" wrote the translator of Burkhardt’s German treatise
Theory of Functions of a Complex Variable (1913, p. 15). He translated Burkhardt’s arcus
as amplitude. G. H. Hardy also chose amplitudein his
Course of Pure Mathematics (1908, p. 82), apparently to keep argument for an independent variable.
For the second the OED gives a quotation from the 1879
edition of the Encyclopedia Britannica,
"In each case u is the
independent variable or argument of the function." A JSTOR search found Gompertz writing in
1825, "These tables represent the logarithm of the present values of
annuities for every value of a certain argument." ("On the
Nature of the Function Expressive of the Law of Human Mortality, and on a New
Mode of Determining the Value of Life Contingencies"
Abstracts of Papers printed in the Philosophical
Transactions of the Royal Society vol. 2, p. 253.)
This entry was contributed by John Aldrich. See also ABSOLUTE VALUE, ARGAND DIAGRAM and MODULUS.
ARITHMETIC is a Greek word transliterated into English as arithmetike. Arithmetike derives from arithmos,
the word for number and it
passed into Latin as arithmetica. Smith (vol. 2, page 7) writes that the Greeks used
arithmetike for the theory of numbers and logistike (logistic) for the art of
calculating. In modern English the more aristocratic name is applied to both
disciplines and most often to the more practical one. See the entry NUMBER THEORY.
Smith (vol. 2, page 8) describes some of the confusions around the word’s spelling:
The word
"arithmetic," like most other words, has undergone many vicissitudes.
In the Middle Ages, through a mistaken idea of its etymology, it took an extra r, as if it had to do with
"metric." So we find Plato of Tivoli, in his translation (1116) of
Abraham Savasorda, speaking of "Boetius in arismetricis." The title
of the work of Johannes Hispalensis, a few years later (c. 1140), is given as
"Arismetrica," and fifty years later than this we find Fibonacci dropping
the initial and using the form "Rismetirca." The extra r
is generally found in the Italian literature until the time of
printing. From Italy it passed over to Germany, where it is not
uncommonly found in the books of the 16th century, and to France, where
it is found less frequently. The ordinary variations in spelling have
less significance, merely illustrating, as in the case with many other
mathematical terms, the vagaries of pronunciation in the uncritical
periods of the world's literatures.
ARITHMETIC MEAN. The arithmetic
mean was one of the three means studied by the Pythagoreans in Antiquity. See
MEAN.
A Google print search by James A. Landau
finds arithmetical mean in 1687 in The Gaugers Magazine, Wherein the Foundation of his Art is briefly Expalin’d and
Illustrated with such Figures as may render the Whole intelligible to a mean
Capacityby William Hunt, Gauger:
Take an Arithmetical mean between GH and CD, Diameters at the Top and Bottom
of the Crown, viz. VW, and multiply the Area answerable thereto by IF the
Altitude of that Segment, the Product is the Content of GHDC from which subduct
the Content of the Crown CFD, the remainder is the Liquor lying about the Crown
when just covered, which added to the upper part, the Sum is the Content of the
whole Copper.
The arithmetic mean has played an important role in the combination
of observations since the time of Galileo. In the Theoria Motus (Theory
of the Motion of Heavenly Bodies moving around the Sun in Conic Sections) (1809,
p. 244) Gauss took it as axiomatic that the
arithmetic mean affords the most probable value ("valorem maxime probabilem")
of the unknown. This has been called the postulate of the arithmetic mean
(E. T. Whittaker & G. Robinson Calculus of Observations (1924, p.
215)) Gauss found that the postulate implied that the errors follow the normal
distribution. See ERROR, NORMAL, and GAUSSIAN.
See also AVERAGE and MEAN.
The term ARITHMETIC PROGRESSION was used by Michael Stifel in
1543: "Divisio in Arethmeticis progressionibus respondet
extractionibus radicum in progressionibus Geometricis" [James A.
Landau].
Arithmetic series is found in 1723 in A System of the Mathematics James Hodgson [Google print search, James A. Landau].
ARITHMETIZATION. Arithmeticize is found in 1859 in Pestalozzi
and Pestalozzianism : life, educational principles, and methods, of John Henry
Pestalozzi, with biographical sketches of several of his assistants and disciples
/ reprinted from the American journal of education edited by Henry Barnard:
"[number] alone leads to infallible results; and, if geometry makes the
same claim, it can be only be means of the application of arithmetic, and in
conjunction with it; that is, it is infallible, as long as it arithmeticizes"
[University of Michigan Digital Library].
Arithmetisirung is found in 1879 in a review of McColl's "Calculus
of Equivalent Statements," Proc. LMS, vol X, pp 16-28:
In diesem dritten Artikel (die frueheren s.F.d.M. X. 34,
JFM10. 0034.02) setzt Herr McColl seine zuerst unter dem Namen "Symbolical
Language" veroeffentlichte und zunaechst zur Verwendung auf mathematische
Probleme bestimmte Arithmetisirung der Logik fort und bringt sie zu einem gewissen
Abschluss. (JFM11.0049.01)
Arithmetisierung appears in an 1887 essay by Leopold Kronecker (1823-1891)
"Ueber den Zahlbegriff" in Crelle's Journal 101 (in Werke
p. 253):
... ich glaube auch, dass es dereinst gelingen wird, den gesammten Inhalt aller
dieser mathematischen Disciplinen zu "arithmetisiren", d.h. einzig
und allein auf den im engsten Sinne genommenen Zahlbegriff zu gruenden, also
die Modificationen und Erweiterungen dieses Begriffs wieder abzustreifen ...
Arithmetize is found in English in 1892 in H. B. Fine in Bull. N.Y.
Math. Soc. I. 175: "It is not merely that the purely arithmetical problems
growing out of algebra were attractive to him [sc. Kronecker] -- he 'arithmetized'
algebra itself" [OED2].
The phrase Arithmetisirung der Mathematik is the title of Felix Klein’s 1895 address before the Royal Society of Sciences
in Goettingen Gesammelte mathematische
Abhandlungen 2 p. 232. [Julio González Cabillón, Michael Detlefsen].
G. U. Yule introduced the term ASSOCIATION of attributes
to "distinguish it from the 'correlation' of continuous variables" (p. 257n) in 1900
("On the
Association of Attributes in Statistics,"
Philosophical Transactions of the Royal Society of London, Ser. A, 194,
257-319.) (David, 1998.)
See CORRELATION.
ASSOCIATIVE "seems to be due to W. R. Hamilton" (Cajori 1919, page 273). Hamilton used the term
as follows:
However, in virtue of the same definitions, it will be found
that another important property of the old multiplication is preserved, or extended
to the new, namely, that which may be called the associative character
of the operation....
The citation above is from
"On a new Species of Imaginary
Quantities connected with a theory of Quaternions" Royal Irish Academy, Proceedings,
Nov. 13, 1843, vol. 2, 424-434.
In his biography of Hamilton, Thomas Hankins discusses this paper:
This paper is marked as having been communicated on Nov.
13, 1843, but it closed with a note that it had been abstracted from a
larger paper to appear in the Transactions of the academy
(Math. Papers, 3:116). That longer paper, also dated Nov. 13, 1843 was
not published until 1848, and when it did appear it concluded with a
note mentioning works written as late as June 1847 ("Researches
respecting Quaternions: First Series," Royal Irish Academy,
Transactions 21, [1848]: 199-296, in Math. Papers, 3:159-216,
"note A," pp. 217-26). In a note Hamilton stated that his presentation
on Nov. 13, 1843 had been "in great part oral" (Math. Papers, 3:225);
therefore it is possible that his statement of and naming of the
associative law was added later when his original communication was to
be printed in 1844. It is thus possible that he first recognized the
importance of the associative law in 1844, when he began work on
Graves's octaves.
The citation above is from Sir William Rowan Hamilton, by
Thomas Hankins, chapter 23 ("The Fate of Quaternions").
(These citations were provided by David Wilkins.)
ASTROID. According to E. H. Lockwood (1961):
The astroid seems to have acquired its present name only
in 1838, in a book published in Vienna; it went, even after that time,
under various other names, such as cubocycloid, paracycle,
four-cusp-curve, and so on. The equation x2/3 +
y2/3 == a2/3 can, however, be
found in Leibniz's correspondence as early as 1715.
This quote was taken from Xah Lee's Visual Dictionary of Special Plane
Curves website.
ASYMPTOTE was used by Apollonius, with a broader meaning than
its current definition, referring to any lines which do not meet, in
whatever direction they are produced (Smith).
The first citation of the word in the OED is in 1656 in Hobbes'
Elements of Philosophy by Thomas Hobbes:
"Asymptotes..come still nearer and nearer, but never touch."
ASYMPTOTIC in the sense of "pertaining to large-sample
behaviour" only became current in Statistics in the 1940s, although asymptotic
arguments had been used for centuries. A JSTOR search produced the following:
asymptotic distribution in S. S. Wilks "Shortest Average Confidence
Intervals from Large Samples" Annals of Mathematical Statistics,
9, (1938), pp. 166-175, asymptotically normal in A. M. Mood "The
Distribution Theory of Runs" Annals of Mathematical Statistics, 11,
(1940), pp. 367-392 asymptotic efficiency in M. S. Bartlett "On
the Theoretical Specification and Sampling Properties of Autocorrelated Time-Series"
Supplement to the Journal of the Royal Statistical Society, 8,
(1946), pp. 27-41.
These were new names for established concepts. However asymptotic relative
efficiency was a new concept, introduced and named by E. J. G. Pitman in
lectures given in 1948. The term appears in G. E. Noether's "Asymptotic Properties
of the Wald-Wolfowitz Test of Randomness" Annals of Mathematical Statistics,
21, (1950), pp. 231-246. [John Aldrich, using David (2001)]
See NORMAL, EFFICIENCY, HYPOTHESIS & HYPOTHESIS TESTING, SMALL SAMPLE.
AUGMENTED MATRIX is found in an 1861 paper by Henry Smith, "On
systems of linear indeterminate equations and congruences,"
Philosophical
Transactions, vol cli, 293-326.
“If to this matrix we add an additional vertical column, composed of the absolute terms of the equations,
the resulting matrix we shall term (for brevity) the augmented matrix of the system.”
[Rod Gow]
AUTOCORRELATION FUNCTION in N. Wiener's Extrapolation, Interpolation and Smoothing of
Stationary Time Series (1949) refers to a function which was prominent but unnamed in his
"Generalized Harmonic Analysis" of 1930 (Acta Mathematica, 55, 117-258) and
in writings back to 1926. The term "auto-correlation" appears in 1933 in a report of a paper
by H. T. Davis (Econometrica, 1, 434) which discusses Wiener's work. Wiener's
function was not strictly a correlation for it was not mean-corrected or normalised; it was
also defined in continuous time. The AUTOCORRELATION COEFFICIENT of H. Wold's (A Study
in the Analysis of Stationary Time Series (1938)) was mean-corrected and normalised and defined
for processes in discrete time. The earlier "serial correlation coefficient" has also survived [John Aldrich].
See STOCHASTIC PROCESS and SERIAL CORRELATION.
AUTOLOGICAL and HETEROLOGICAL. The
OED’s earliest citation is F. P. Ramsey writing in the Proceedings
of the London Mathematical Society, 25, (1926), 358: “Let us call
adjectives whose meanings are predicates of them, like ‘short’, autological;
others heterological.” The terms derived from the German autologisch
and heterologisch introduced by K. Grelling and L. Nelson “Bemerkungen
zu den Paradoxien von Russell und Burali-Forti” Abhandlungen der Fries’schen
Schule II, Göttingen 1908, S. 301-334. See Wikipedia
on The
Grelling-Nelson paradox.
AUTOMORPHIC FORM, AUTOMORPHIC FUNCTION. These terms were used by Felix Klein in 1890 in
“zur Theorie der Laméschen Functionen”
in the 1890 issue of Nachrichten von der Königlichen Gesellschaft
der Wissenschaften und der Georg-Augusts-Universität zu Göttingen.
Automorphe Functionen appears once, on page 94:
Bekanntlich sind λ und √f(λ) in
dem soeben gefundenen η eindeutig; sie stellen
solche eindeutige Functionen von η vor, welche sich bei unendlich
vielen linearen Substitutionen von η reproduciren (ich möchte
vorschlagen, solche Functionen überhaupt automorphe Functionen von η zu
nennen).
Babelfish translates this as “I would like to suggest, such
Functionen at all automorphe Functionen of η to call.”
Aautomorphe Formen appears once, on page 95:
Bei diesen bleiben dann, λ1, λ2 ungeändert;
ich schlage dementsprechend vor, dieselben als automorphe Formen von F1, F2
zu bezeichnen.
Babelfish translates this as “With these remain then λ,
λ ungeandert I suggest accordingly calling the same as
automorphe forms of F.”
Klein also used both automorphe functionen and automorphe formen in
Vorlesungen über die Theorie der elliptischen Modulfunctionen (1890), with a footnote reading:
Hr. Poincaré hat über die gedachten Functionen
ausser einer grossen Reihe kleinerer mit dem Jahre 1881 beginnender
Noten in der Comptes Rendus zunächst 1881 einen Aufsatz in den
Mathematischen Annalen (Bd. 19: Sur les fonctions uniformes qui se
reproduisent par des substitutions linéaires) ..
Hr. Klein bezeichnet die hier in Betracht kommenden Functionen
neuerdings als linear-automorphe Functionen oder wohl auch kurzweg als
automorphe Functionen.
The 1892 issue of Nachrichten pages 283 – 291 has a paper by Klein
“Die Eindeutigen automorphen Formen vom Geschlechte Null” (pp. 283-91)
in which he uses automorphen Formen, automoörphe Functionen, and two new expressions, automorphe Inegrale and automorphe Reihe.
Furthermore he refers to Poincaré several times and refers to Poincarésche Reihe.
Automorphic function appears in English in 1892 in the Bulletin of the New York Mathematical Society:
“The theory of automorphic functions, recently developed by
Poincare and Klein, affords instances of analytic functions with
natural boundaries....”
[This entry was contributed by James A. Landau.]
AUTOMORPHIC TRANSFORMATION. Automorphic transformations appear to have been first investigated by Hermite, who
called them (in French) transformation en elle-meme, which translates into English as “transformation into itself.”
In “Remarques sur un memoire de M. Cayley relative aux Determinants Gauches” in
the Cambridge and Dublin Mathematical Journal
(1854), Hermite wrote “Je me propose de donner içi des
formules analogues à celles de M. Cayley, pour la transformation
en elle-même d’une
forme quadratique quelconque.” [I propose to give here formulas
analogous to those of Mr. Cayley for the transformation into itself of
any quadratic form whatsoever.]
Cayley used transformation en elle-même in a French-language paper he wrote in 1855, but used automorphic transformation when writing in English in 1858.
It is not clear whether Cayley introduced the term automorphic transformation into English or whether he was using an existing term.
[This entry was contributed by James A. Landau.]
AUTOMORPHISM was used by H. J. Stephen Smith in “Report on the Theory of Numbers—Part III,”
which appeared in 1862 in the published Report of the Thirty-First Meeting of the British Association for the Advancement of Science.
AUTOREGRESSION and AUTOREGRESSIVE PROCESS derive from H. Wold's "process
of linear autoregression" (A Study in the Analysis of Stationary Time
Series (1938)) which referred to processes of the type analysed by G. U. Yule in
"On a Method of
Investigating Periodicities in Disturbed
Series, with Special Reference to Wolfer's Sunspot Numbers,"
Phil. Trans. Royal Society, 226A, (1927), 267-298. Long before
Yule, in 1877, Galton used the first-order process to model inheritance.
(David, 2001)
The multivariate generalisation was considered by H. B. Mann
& A. Wald “On the Statistical Treatment of Linear Stochastic Difference Equations,”
Econometrica, 11, No. 3/4, (1943), 173-220. A JSTOR search found the term
vector autoregressive process in D. F. Hendry “Maximum Likelihood Estimation of Systems
of Simultaneous Regression Equations with Errors Generated by a Vector Autoregressive Process,”
International Economic Review, 12, No. 2. (1971), 257-272.
See REGRESSION, YULE-WALKER EQUATIONS and STOCHASTIC PROCESS.
AVERAGE, according to the OED, appeared in English around 1500 originally in connection
with maritime trade in the Mediterranean. The dictionary gives a list of successive meanings of the term, as follows:
(1) Originally an impost on goods. (1502)
(2) Any charge in excess of the freight charges, payable by the owner of the goods. (1491)
(3) Loss to the owners from damage at sea. (1611)
(4) Equitable distribution of such expense, when shared by a group. (1598)
(5) Distribution of the aggregate inequalities of a series of things. (1735)
(6) The arithmetic mean so obtained, the medium, amount, the "common run." (1755)
The year is that of the earliest quotation the dictionary gives for that particular usage.
(Based on the entry "Average" in Walker (1929, p. 176))
Average is often used as an alternative for both mean (in
general) and arithmetic mean. Like mean, it is often used in the sense of "expected
value."
See ARITHMETIC MEAN, MEAN, CENTRAL TENDENCY and also Symbols in
Statistics on the Symbols in Probability and Statistics page.
AVOIRDUPOIS. From Smith vol. 2, page 639:
The word "avoirdupois" is more properly spelled
"averdepois," and it so appears in some of the early books. It comes
from the Middle English aver de poiz, meaning "goods of
weight." In the 16th century it was commonly called "Haberdepoise,"
as in most of the editions of Recorde's (c. 1542) Ground of
Artes. Thus in the Mellis eddition of 1594 we have: "At London
& so all England thorugh are vsed two kids of waights and
measures, as the Troy waight & the Haberdepoise."
The term AXIOM (in Greek, 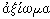 )
was used by the Stoic philosophers and by Aristotle, although, according
to W. & M. Kneale The Development of Logic (1962) p. 145, the Stoic
usage does not correspond to the modern "axiom" but to "judgement"
or "proposition."
)
was used by the Stoic philosophers and by Aristotle, although, according
to W. & M. Kneale The Development of Logic (1962) p. 145, the Stoic
usage does not correspond to the modern "axiom" but to "judgement"
or "proposition."
In Euclid's
Elements
what would now be called "axioms" are designated either as "common
notions" or as "postulates." See the
list.
Kline (p. 59) explains that "the common notions are truths applicable to all sciences, whereas the postulates
apply only to geometry." The term "axiom" is not used but in
the notes to his edition of the Elements T. L Heath (1926, vol. 1, pp.
120-1) observed that Aristotle used a similar construction to "common notions"
as an alternative expression for "axioms." Proclus, an important commentator
on the Elements from the 5th century AD, used "axioms."
The OED records the English word axiom in 1485 used in the sense of “a
proposition that commends itself to general acceptance.” The word came into
English from the Greek via Latin and French.
See POSTULATE.
AXIOM OF ARCHIMEDES. According to a message to a math history mailing
list by Yaakov Kupitz, an extended account of the axiom of Archimedes is given
by F. Enriques: "Prinzipien der Geometrie" in
Encyklopadie
der Mathematischen Wissenschaften. Bd. 3, T.1,
H.1, pp. 34ff. From this we learn that the erroneous name "axiom
of Archimedes" was given by Stolz "Zur Geometrie der Alten, insbesondere über ein Axiom des Archimedes,"
Mathematische
Annalen, 22, (1883), 504-519.
The suggestion that the axiom be attributed, instead, to Eudoxos was made by
Zeuthen at the Heidelberg congress of mathematics (circa 1900), p. 541 of the
congress volume. Today Zeuthen's suggestion is universally accepted.
AXIOM OF CHOICE. In 1904 in "Beweis, dass jede Menge wohlgeordnet
werden kann" ["Proof that every set can be well-ordered"],
Mathematische
Annalen, 59, 514-6. Ernst
Zermelo used the Axiom of Choice to prove that every set can be well-ordered.
Zermelo did not use the name "Axiom of Choice". Rather he stated:
The present proof rests upon the assumption that coverings gamma actually do
exist, hence upon the principle that even for an infinite totality of sets there
are always mappings that associate with every set one of its elements, or, expressed
formally, that the product of an infinite totality of sets, each containing
at least one element, itself differs from zero. This logical principle cannot,
to be sure, be reduced to a still simpler one, but it is applied without hesitation
everywhere in mathematical deduction.
"gamma" is defined earlier in the paper by
Imagine that with every subset M' there is associated an arbitrary element
m'1 that occurs in M' itself...This yields a "covering"
gamma of the [set of all subsets M'] by certain elements of the set M.
Zermelo adds "I owe to Mr. Erhard Schmidt the idea that, by invoking this
principle, we can take an arbitrary covering gamma as a basis for the well-ordering."
In the paper "Untersuchungen über die Grundlagen der Mengenlehre I"
["Investigations in the foundations of set theory I"], Mathematische
Annalen, 65, 261-281 Zermelo
presents a set of axioms for set theory. (This paper is generally dated 1908
in bibliographies, presumably because that was the year it appeared in Mathematische
Annalen, but the paper is dated "Chesières, 30 July 1907.") In
this paper there appears:
AXIOM VI. (Axiom of choice). If T is a set whose elements all are sets that
are different from 0 and mutually disjoint, its union "union of T"
includes at least one subset S1 having one and only one element in
common with each element of T. [The original German read "Axiom der Auswahl".]
In another paper also published in 1908, " Neuer Beweis für die Möglichkeit
einer Wohlordnung" ["A new proof of the possibility of a well-ordering"],
Mathematische
Annalen, 65, 107-28, Zermelo writes
Now in order to apply our theorem to arbitrary sets, we require only the additional
assumption that a simultaneous choice of distinguished elements is in principle
always possible for an arbitrary set of sets
IV. Axiom. A set S that can be decomposed into a set of disjoint parts A, B,
C..., each containing at least one element, possesses at least one subset S1
having exactly one element in common with each of the parts A,B,C,... considered.
In the same paper Zermelo adds:
Even Peano's Formulaire, which is an attempt to reduce all of mathematics
to "syllogisms" (in the Aristotelian-Scholastics sense), rests upon
quite a number of unprovable principles; one of these is equivalent to the principle
of choice for a single set and can then be extended syllogistically to an arbitrary
finite number of sets.
All of the above material is from Heijenoort (1967). The translations of Zermelo
in this book are by Stefan Bauer-Mengelberg.
In 1908 Bertrand Russell wrote in his "Mathematical Logic as Based on
the Theory of Types," American Journal of Mathematics, 30,
222-262
Many elementary theorems concerning cardinals require the use of the multiplicative
axiom [i.e. the axiom that, given a set of mutually exclusive classes, none
of which are null, there is at least one class consisting of a member from each
class in the set]. It is to be observed that this axiom is equivalent
to Zermelo’s, and therefore to the assumption that every class can be well ordered.
These equivalent assumptions are, apparently, all incapable of proof, though
the multiplicative axiom, at least, appears highly self-evident. (pp. 258-9)
According to Grattan-Guinness (2000, p. 341) Russell discovered the multiplicative
axiom in 1904 "slightly before the conception and writing of Zermelo’s
paper, so reversing the priority over finding Russell’s paradox." See RUSSELL'S
PARADOX.
The axiom of choice was first used in set theory and the theory of transfinite
numbers but it was soon applied to other branches of mathematics. The HAUSDORFF
PARADOX was an early example (1914). Many of the applications were due
to Polish mathematicians with
Wacław
Sierpiński in the lead: see e.g. his "Sur le rôle de l'axiome
de M. Zermelo dans l’analyse moderne,"
Comptes
Rendus, 163, (1916), 688-691.
Gregory Moore Zermelo's Axiom of Choice: Its Origins, Development and Influence
(1982, chapters 3 & 4) discusses these applications. A related development
was the development of more immediately applicable versions of the axiom. See
ZORN’S LEMMA.
For a long time a reference to Zermelo was mandatory
as in “the Zermelo Axiom of Choice” in E. W. Chittenden and A. D. Pitcher “On
the Theory of Developments of an Abstract Class in Relation to the Calcul
Fonctionnel,” Transactions of the American Mathematical Society, 20,
(3), (1919), p. 215. But eventually the simple axiom of choice became
acceptable; see e.g. Sierpiński’s
“Les exemples
effectifs et l'axiome du choix,” Fundamenta Mathematicae, 2,
(1921), 112-118.
This article was contributed by James A. Landau.
AXIS occurs in English in the phrase "the Axis or Altitude of
the Cone" in 1571 in A Geometricall Practise named Pantometria
by Thomas Digges (1546?-1595) (OED2).
Front -
A -
B -
C -
D -
E -
F -
G -
H -
I -
J -
K -
L -
M -
N -
O -
P -
Q -
R -
S -
T -
U -
V -
W -
X -
Y -
Z -
Sources
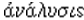 derived from the verb
derived from the verb  to unloose, undo. T. Heath writes in A History of Greek Mathematics, volume 1 (1921, p. 291), “analysis [was] according to the ancient view nothing more
than a series of successive reductions of a theorem or a problem till it is
finally reduced to a theorem or problem already known.” Kline (page 279)
states that the term was introduced by
Theon of Alexandria.
to unloose, undo. T. Heath writes in A History of Greek Mathematics, volume 1 (1921, p. 291), “analysis [was] according to the ancient view nothing more
than a series of successive reductions of a theorem or a problem till it is
finally reduced to a theorem or problem already known.” Kline (page 279)
states that the term was introduced by
Theon of Alexandria.
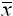 is the same as that of y, η, y,
is the same as that of y, η, y, 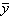 .” [James A. Landau]
.” [James A. Landau]
 )
was used by the Stoic philosophers and by Aristotle, although, according
to W. & M. Kneale The Development of Logic (1962) p. 145, the Stoic
usage does not correspond to the modern "axiom" but to "judgement"
or "proposition."
)
was used by the Stoic philosophers and by Aristotle, although, according
to W. & M. Kneale The Development of Logic (1962) p. 145, the Stoic
usage does not correspond to the modern "axiom" but to "judgement"
or "proposition."