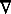Earliest Known Uses of Some of the Words of Mathematics (D)

Last revision: Jan. 4, 2018

The DANIELL INTEGRAL was introduced by Percy John Daniell in “A General Form of Integral,” Annals of Mathematics, 19, (1918), 279-294. See the entry in Encyclopedia of Mathematics. The first person to use the Daniell Integral and to refer to it as such was Norbert Wiener “The Mean of a Functional of Arbitrary Elements,” Annals of Mathematics, 22, (1920), 66-72.

DANIELL WINDOW or Daniell kernel refers to a device used for smoothing the PERIODOGRAM to obtain an estimate of the SPECTRAL DENSITY that was proposed by Percy John Daniell in a written contribution to the discussion in the “Symposium on Autocorrelation in Time Series,” Journal of the Royal Statistical Society, Supplement, 8, (1946), 88-90.

A Google print view shows a use of Daniel’s window which seems to be from 1958, but because only snippet view is available the date is uncertain. Gravity Measurements in Western Greenland, B. Lunos bogtr., Geodætisk institut (Denmark): “Cross correlation magnitude, cross power, coherency and phase have been computed with the aid of Daniell’s window using different components of noise at the same station and also with like components from different stations.” [Google print search by James A. Landau]

A JSTOR search found the phrase “the Daniell window” in M. B. Priestley “Evolutionary Spectra and Non-Stationary Processes,” Journal of the Royal Statistical Society, B, 27, (1965), p. 220.

The term Daniell kernel is found in what appear to be documents from 1985 and 1987. [Google print search by James A. Landau]

See the entries WINDOW and KERNEL.

DATA ANALYSIS. This term had been used casually for decades before John W. Tukey made it his own in "The Future of Data Analysis," Annals of Mathematical Statistics, 33, (1962), 1-67. It is not exactly clear what Tukey meant by data analysis and how it was different from statistics but he quietly condemns a lot of statistical research. The paper concludes with the proposition that the future of data analysis depends on "our willingness to take up the rocky road of real problems in preference to the smooth road of unreal assumptions, arbitrary criteria, and abstract results without real attachments." (p. 64)

See STATISTICS and EXPLORATORY DATA ANALYSIS.

DATA MINING. Cheap computing has made it possible for statisticians and other researchers to investigate alternative specifications and generally search for patterns in their data. In the 40 or so years that the term data mining has been in use the scope of the activity and its status have changed considerably. A JSTOR search found this from 1962 "after a shameless amount of data-mining my best candidate [equation] is ..." A. M. Okun "The Predictive Value of Surveys of Business Intentions," American Economic Review, 52, Papers and Proceedings of the Seventy-Fourth Annual Meeting of the AEA, p. 223. More recently D. J. Hand, G. Blunt, M. G. Kelly & N. M. Adams write in their "Data Mining for Fun and Profit," Statistical Science, 15, (2000), 111-126, "Data mining is the process of seeking interesting or valuable information in large data bases. ... [It] is an interdisciplinary subject, representing the confluence of ideas from statistics, exploratory data analysis, machine learning, pattern recognition, database technology, and other disciplines." (p. 111)

DECAGON. A Google print search shows what appear to be latus decagon and decagon equilaterus in a 1509 Latin translation of Euclid’s Elements by Luca Pacioli. [Google print search by James A. Landau]

Decagon appears in English in 1571 in A geometrical practise named Pantometria by Thomas Digges (1546?-1595) (although the spelling decagonum is used).

DECILE (in statistics) was introduced by Francis Galton (Hald, p. 604).

Decile appears in 1882 in Francis Galton, Rep. Brit. Assoc. 1881 245: "The Upper Decile is that which is exceeded by one-tenth of an infinitely large group, and which the remaining nine-tenths fall short of. The Lower Decile is the converse of this" [OED].

A Google print search by James A. Landau finds pre-1882 uses of decile in astronomy and astrology.

DECIMAL is derived from the Latin decimus, meaning "tenth." According to Smith (vol. 2, page 14), in the early printed books numbers which are multiples of 10 were occasionally called decimal numbers, citing Pellos (1492, fol. 4), who speaks of "numbre simple," "nubre desenal," and "nubre plus que desenal" and Ortega (1512, 1515 ed., fols. 4, 5), who has "lo numero simplice," "lo numero decenale," and "lo numero composto."

In 1603 Johann Hartmann Beyer published Logistica Decimalis.

Decimal occurs in English in 1608 in the title Disme: The Art of Tenths, or Decimall Arithmetike. This work is a translation by Robert Norman of La Thiende, by Simon Stevin (1548-1620), which was published in Flemish and in French in 1585.

DECIMAL POINT. In 1617 in his Rabdologia John Napier referred to the period or comma which could be used to separate the whole part from the fractional part, and he used both symbols.

The 1689 edition of Mr. Wingate’s Arithmetick has: “A Decimal fraction may be express’d without the Denominator, by prefixing a point or comma before (to wit, on the left hand of) the Numberator, so 5/10 may be written thus, .5 or thus, ,5, and 25/100 thus, ,25, or thus, 25 [sic, should read “thus, .25”].” [Google print search by James A. Landau]

In 1704 the term Separating Point is used in the Lexicon Technicum in the entry "Decimal."

In 1705 Stereometry, Or, the ART of GAUGING, 5th ed., by Thomas Everard has: “A Decimal Fraction, whether it stand alone or be join’d with whole Numbers, is distinguished from a whole Number by a point or prick before it towards the left hand, as in these Examples.” [Google print search by James A. Landau]

According to Cajori (vol. 1, page 329), "Probably as early as the time of Hutton the expression ‘decimal point’ had come to be the synonym for ‘separatrix’ and was used even when the symbol was not a point."

Decimal point appears in the 1771 edition of the Encyclopaedia Britannica in the article "Arithmetick": "The point thus prefixed is called the decimal point" [James A. Landau].

In 1863, The Normal: or, Methods of Teaching the Common Branches, Orthoepy, Orthography, Grammar, Geography, Arithmetic and Elocution by Alfred Holbrook has: "The separatrix is the most important character used in decimals, and no pains should be spared to impress this on the minds of pupils."

DECIMAL SYSTEM is found in English in 1811 in An Elementary Investigation of the Theory of Numbers by Peter Barlow [James A. Landau].

DECISION PROBLEM (in mathematical logic) from the German das Entscheidungsproblem. According to S. C. Kleene Introduction to Metamathematics, (1952, p. 136), “the decision problem … appears in modern logic with Schröder 1895, Löwenheim 1915 and Hilbert 1918.” The term Entscheidungsproblem is in the title of H. Behmann’s “Beiträge zur Algebra der Logik, insbesondere zum Entscheidungsproblem,” Mathematische Annalen 86, (1922), 163-239.

The German term appears in English texts, not only in early works like Alonzo Church’s “A Note on the Entscheidungsproblem,” Journal of Symbolic Logic, 1, (1936), 40-41 or A. M. Turing’s “On Computable Numbers with an Application to the Entscheidungsproblem,” Proceedings of the London Mathematical Society, 32, (1937), 232-265, but, more surprisingly, in modern works. There has long been an acceptable English term, “decision problem,”—see e.g. C. H. Langford Journal of Symbolic Logic, 1, (1936), p. 111—but the two terms seem to co-exist quite happily.

See TURING MACHINE.

Statistical DECISION THEORY was essentially a 20^th century development although some of the ideas can be found in earlier work: see MEAN ERROR. The theory exists in both classical and Bayesian versions.

The classical theory was founded by Abraham Wald in 1939 ("Contributions to the Theory of Statistical Estimation and Testing Hypotheses," Annals of Mathematical Statistics, 10, 299-326) and developed in his book Statistical Decision Functions (1950).

The phrase "decision theory" appears in E. L. Lehmann’s "Some Principles of the Theory of Testing Hypotheses," Annals of Mathematical Statistics, 21, (1950), 1-26.

The first full presentation of the Bayesian theory was Howard Raiffa & Robert Schlaiffer’s Applied Statistical Decision Theory (1961). The phrase "Bayesian decision theory" appeared in the titles of two papers presented at the 1961 ASA conference see American Statistician, 15, (Oct., 1961), p. 25 [John Aldrich].

See also ADMISSIBILITY, BAYES ESTIMATE, BAYES RISK, LOSS FUNCTION, RISK FUNCTION, MINIMAX.

DEEP (theorem). From its beginnings in Old English as a spatial term, the adjective deep has acquired numerous figurative meanings; see the OED for details. In contemporary mathematics it is often applied to theorems: “A theorem is deep whose proof is long, complicated, difficult, or appears to involve branches of mathematics which are not obviously related to the theorem itself.” D. Shanks Solved and Unsolved Problems in Number Theory, 4th ed. (1993, p. 64).

The Hardy-Littlewood school of analytic number theory were perhaps the first to use deep in the most esoteric of its mathematical senses: for example, “It appears probable that such a result cannot really be as deep as the prime number theorem, but nobody has succeeded up to now in proving it by elementary reasoning.” writes S. Ramanujan “Highly Composite Numbers,” Proceedings of the London Mathematical Society (1915), 14, (1), p. 386n. Here elementary reasoning means reasoning using only concepts from the branch of mathematics to which the theorem relates and, in particular, not using complex analysis to prove results about prime numbers. See PRIME NUMBER THEOREM.

The phrase deep theorem seems to have come into print around 1930. “It is possible, at heavy cost, to improve slightly upon the theorem [...] but I am not aware that a proof has been given without employing [...] a deep theorem due to Walfisz.” writes J. R. Wilton “A Series of Bessel Functions Connected with the Lattice-Points of an n-Dimensional Ellipsoid”, Proceedings of the Royal Society A, 120, (Sept. 1928), p. 361.

[This entry was contributed by John Aldrich.]

The term DEFINITE INTEGRAL was apparently introduced by Laplace. It appears in his "Memoire sur les suites" pp. 207-309 Histoire de l'Académie Royale des Sciences. Paris, 1782 (year 1779). p. 209: "je nomme intégrale définie, une intégrale prise depuis une valeur déterminée de la variable jusqu'à une autre valeur déterminée." [Udai Venedem]

The term definite integral is defined by Sylvestre-François Lacroix (1765-1843) in Traité du calcul différentiel et integral, Tome second (1798) (Cajori 1919, page 272.)

Augustin Louis Cauchy (1789-1857) used the term. It is found in his "Intégrales définies," Oeuvres (2), IV, 125: "This limit is called a definite integral."

Definite integral is found in English in 1831 in Elements of the Integral Calculus (1839) by J. R. Young:

Thus, if we know that for x = a the value of the integral Fx + C ought to be A, then we have Fa + C = A, therefore the value of the constant is in that case C = A - Fa, so that the definite integral, as it is then called, is Fx + A - Fa.

In 1922 Introduction to the Calculus by William F. Osgood has "Thus the definite integral is, by definition, the limit of a sum...."

Although modern textbooks generally define definite integral as the limit of a sum, Webster’s Third New International Dictionary (1961), defines it as "the number obtained by finding an antiderivative of a function, substituting for the variable the first of two given numbers, then the second, and subtracting the second result from the first."

DEGREE (angle measure) is found in English in about 1386 in Chaucer’s Canterbury Tales: "The yonge sonne That in the Ram is foure degrees vp ronne" [OED]. He again used the word in about 1391 in A Treatise on the Astrolabe: "9. Next this folewith the cercle of the daies, that ben figured in manere of degres, that contenen in nombre 365, dividid also with longe strikes fro 5 to 5, and the nombre in augrym writen under that cercle."

DEGREE (of a polynomial). See order.

DEGREES OF FREEDOM. The term degrees of freedom is found in a non-statistical sense in, for example, 1867 in Treatise on Natural Philosophy by Sir William Thomson and Peter Guthrie Tait: “Several references have been made in preceding sections to the number of independent variables in a displacement, or to the degrees of freedom or constraint under which the displacement takes place. ... A free point has three degrees of freedom, inasmuch as the most general displacement which it can take is resolvable into three, parallel respectively to any three directions, and independent of each other.” [Google print search by James A. Landau]

Fisher introduced degrees of freedom in connection with Pearson’s χ² test in the 1922 paper “ On the Interpretation of χ² from Contingency Tables, and the Calculation of P,” J. Royal Statist. Soc., 85, pp. 87-94. He applied the number of degrees of freedom to distributions related to chi-squared--Student’s distribution and his own z distribution in his 1924 paper, “ On a Distribution Yielding the Error Functions of Several Well Known Statistics,” Proceedings of the International Congress of Mathematics, Toronto, 2, 805-813 [John Aldrich].

See also chi-squared, F-distribution and Student’s t-distribution.

DEL (as a name for the symbol 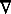) is found in 1901 in Vector Analysis, A text-book for the use of students of mathematics and physics founded upon the lectures of J. Willard Gibbs by Edwin Bidwell Wilson (1879-1964):

There seems, however, to be no universally recognized name for it, although owing to the frequent occurrence of the symbol some name is a practical necessity. It has been found by experience that the monosyllable del is so short and easy to pronounce that even in complicated formulae in which (the symbol) occurs a number of times no inconvenience to the speaker or hearer arises from the repetition [OED].

See NABLA (another name for the same operator) and the Earliest Uses of Symbols of Calculus page.

The term DELTAHEDRON is found in 1871 in A Handbook to the Mineralogy of Cornwall and Devon by J. H. Collins, which has an illustration of a “deltahedron” with the note that it is the crystal form of Garnet, Argentite, and Analcite. [Google print search by James A. Landau]

In 1873 A First Book of Mineralogy by J. H. Collins has several occurences of deltohedron, which is defined as a polyhedron bounded by twenty-four equal deltoids, where a deltoid is defined on page 17 as “a four-sided figure of such a form that one of its diameters will divide it into two equal scalene triangles, and the other into two unequal isosceles triangles.” [Google print search by James A. Landau]

DEMOIVRE’S THEOREM. In his Synopsis Palmariorum Matheseos (1707), W. Jones refers to a "Theorem" of "that Ingenious Mathematician, Mr. De Moivre."

Theorema Moivræanum appears in a review of Jones’s book in Acta Eruditorum (1707).

However, the above use of the term refers to a different theorem from the one now associated with this term, and according to Smith in A Source Book in Mathematics, "The terms De Moivre’s Formula, De Moivre’s Theorem, applied to the formula we are considering, do not seem to have come into general use till the early part of the nineteenth century." The remaining citations pertain to what is now known as Demoivre’s formula.

Demoivre’s formula appears in A. L. Crelle, Lebrbuch der Elemente der Geometrie und der ebenen und spbärischen Trigonometrie, Berlin, vol. I, 1826, according to Tropfke.

The earliest use in English of Demoivre’s formula which unmistakably refers to (cis θ)ⁿ = cis nθ which James A. Landau could find in a Google print search is in 1809 in Treatise on Plane and Spherical Trigonometry by Robert Woodhouse.

The earliest use in English of Demoivre’s theorem which unmistakably refers to (cis θ)ⁿ = cis nθ which James A. Landau could find in a Google print search is in 1812 in A Treatise on Trigonometry and on Trigonometrical Tables and Logarithms by J. Hymers.

DE MORGAN’S LAWS. According to W. & M. Kneale The Development of Logic (1962) p. 295 these were known to medieval logicians and "occur explictly" in William of Ockham’s (c.1287-1347) Summa Totius Logicae. They were rediscovered by Augustus de Morgan (1806-1871) and appear in "On the Symbols of Logic, the Theory of the Syllogism, and in particular of the Copula," Transactions of the Cambridge Philosophical Society, 9, (1850): "The contrary of an aggregate is the compound of the contraries of the aggregants: the contrary of a compound is the aggregate of the contraries of the components." (p. 119 On the Syllogism and Other Logical Writings by Augustus De Morgan edited by Peter Heath.)

The mathematical logicians Peano and Schröder referred to De Morgan. The progress of De Morgan terms in English can be followed through the OED and JSTOR.  The OED quotes C. I. Lewis Survey of Symbolic Logic (1918, p. 125): "3.4 and 3.41 together state De Morgan’s Theorem." The first JSTOR appearance is in 1945 when "De Morgan’s Laws" is an entry in an index in the Journal of Symbolic Logic.

DENSE is found in English in 1902 in Proc. Lond. Math. Soc. XXXIV: "Every example of such a set [of points] is theoretically obtainable in this way. For..it cannot be closed, as it would then be perfect and nowhere dense."

DEPENDENT/INDEPENDENT VARIABLE. Independent variable appears in 1813 in Memoirs of the Analytical Society (Cambridge): “The method of Laplace for reducing an equation of the first order, where the difference of the independent variable is any function of the variable itself, to one wherein that difference is constant, is well known.” [Google print search by James A. Landau]

Subordinate variable and independent variable appear in English in the 1816 translation of Differential and Integral Calculus by Lacroix: "Treating the subordinate variables as implicit functions of the indepdndent [sic] ones" [OED].

Dependent variable appears in in 1831 in the second edition of Elements of the Differential Calculus (1836) by John Radford Young: "On account of this dependence of the value of the function upon that of the variable the former, that is y, is called the dependent variable, and the latter, x, the independent variable" [James A. Landau].

In Statistics R. A  Fisher used the terms dependent and independent in his presentation of regression analysis: see Section 25 of Statistical Methods for Research Workers (1925) on "Regression coefficients". For Fisher these terms qualified variate but later writers have generally favoured variable.

See also REGRESSION.

DERANGEMENT. An early use of this term is in W. A. Whitworth, Choice and Chance, Cambridge, 1870 where it means a nonidentity permutation. P. A. P. MacMahon uses it in its modern sense of a fixed-point-free permutation in “The problem of derangement in the theory of permutations,” Trans. Camb. Phil. Soc., Vol 21, pp. 467-481, 1908. [David Callan]

DERIVATIVE. See the entry DIFFERENTIAL CALCULUS, DERIVATIVE.

DESCARTES’ RULE OF SIGNS. In 1809 The Gentleman’s Mathematical Companion for the year 1798, The Second Edition has “Descartes’ rule.” [Google print search by James A. Landau]

The 1824 Supplement to the Fourth, Fifth, and Sixth Editions of the Encyclopædia Britannica, Volume Fourth, has “rule of Descartes.” [Google print search by James A. Landau]

In 1833 The penny cyclopædia has: “The latter of the two works contains an extension of Descartes’ well known rule of signs, by means of which the number of the real roots of an equation may be determined.” [Google print search]

London and Edinburgh Philosophical Magazine and Journal of Science, Vol. VII, July-December 1835 has “the rule of signs of Descartes.” [Google print search by James A. Landau]

Descartes’ rule of signs is found in English in 1855 in An elementary treatise on mechanics, embracing the theory of statics and dynamics, and its application to solids and fluids. Prepared for the undergraduate course in the Wesleyan university by Augustus W. Smith: "Now, since the degree of the equation is even and the absolute term is negative, there are at least two possible roots, one positive and the other negative. The other two roots may be real or imaginary. If real, Descartes’ rule of signs indicates that three will be positive and one negative" [University of Michigan Digital Library].

The term DESCRIPTIVE GEOMETRY occurs in the title Géométrie Descriptive (1795) by Gaspard Monge (1746-1818).

DESCRIPTIVE STATISTICS. The term entered circulation in the 1920s under the influence of a discussion in J. M. Keynes’s A Treatise on Probability (1921, p. 327).

The first function of [the Theory of Statistics] is purely descriptive. It devises numerical and diagrammatic methods by which certain salient characteristics of large groups of phenomena can be briefly described; […] The second function of the theory is inductive. It seeks to extend its description of certain characteristics of observed events to the corresponding characteristics of other events which have not been observed.

The distinction became established although later writers usually preferred inferential to inductive. Keynes and many of these writers believed that the descriptive function had been over-emphasised.

(The term descriptive statistics is found in use as early as 1835, but not in the modern sense in which it is paired with inferential statistics.)

Compare DATA ANALYSIS and EXPLORATORY DATA ANALYSIS.

DESIGN MATRIX in the analysis of variance and regression. Around 1950 several authors began using matrix formalism in describing the design of experiments. The problem of design was interpreted as the choice of a "design matrix" as in K. D. Tocher’s "The Design and Analysis of Block Experiments," Journal of the Royal Statistical Society B, 14, (1952), p. 48. More recently the term has been used for the X matrix (in the usual formalism) regardless of whether an experiment is involved. E.g. the term has been used in this way by econometricians since the 1970s: see e.g. G. Judge & M. E. Bock "A Comparison of Traditional and Stein-Rule Estimators under Weighted Squared Error Loss." International Economic Review, 17, (1976), p. 238. (JSTOR search)

This entry was contributed by John Aldrich. See the entry ERROR in the usual formalism.

DESIGN OF EXPERIMENTS in Statistics. The phrase and the subject it refers to are associated with the 1935 book by R. A. Fisher, The Design of Experiments, although Fisher had already been working on the subject for more than a decade. His earliest published thoughts are in chapter VIII, section 48, "Technique of Plot Experimentation," of Statistical Methods for Research Workers (1925). He gave a fuller account in "The Arrangement of Field Experiments", Journal of the Ministry of Agriculture of Great Britain, 33, (1926)

Other entries related to the design of experiments: ALIAS, BLOCK, CONFOUNDING, COVARIANCE, COVARIATE, DESIGN MATRIX, EFFECTS, ERROR, FACTOR, LATIN SQUARE, TREATMENT.

The term DESMIC was coined by Cyparissos Stephanos (1857-1918) in "Sur les systemes desmiques de trois tetraedres," published in Darboux’s Bulletin ser 2, vol 3 (1879), pp 424-456 [Julio González Cabillón, Michael Lambrou].

DETERMINANT (discriminant of a quantic) was introduced in 1801 by Carl Friedrich Gauss in his Disquisitiones arithmeticae Werke Bd. 1, p. 122:

Numerum bb — ac, a cuius indole proprietates formae (a, b, c) imprimis pendere in sequentibus docebimus, determinantem huius formae uocabimus.

(Cajori vol. 2, page 88; Smith vol. 2, page 476).

Laplace had used the term resultant in this sense (Smith, 1906).

DETERMINANT (modern sense). Thomas Muir begins his monumental The Theory of Determinants in the Historical Order of Development with Leibniz in 1693 and describes about 20 contributions before he reaches 1812 when Augustin-Louis Cauchy (1789-1857) first used determinant in its modern sense (Schwartzman, page 70). Cauchy employed the word in “Memoire sur les fonctions qui ne peuvent obtenir que deux valeurs egales et des signes contraires par suite des transpositions operees entre les variables qu'elles renferment”, addressed on November 30, 1812, and first published in Journal de l'Ecole Poytechnique, XVIIe Cahier, Tome X, Paris, 1815 Oeuvres (2) i: p. 112. Cauchy refers to Gauss’s use of the term (see preceding entry)

M. Gauss s'en est servi avec avantage dans ses Recherches analytiques pour decouvrir les proprietes generales des formes du second degre, c'est a dire des polynomes du second degre a deux ou plusieurs variables, et il a designe ces memes fonctions sous le nom de determinants. Je conserverai cette denomination qui fournit un moyen facile d'enoncer les resultats; j'observerai seulement qu'on donne aussi quelquefois aux fonctions dont il s'agit le nom de resultantes a deux ou a plusieurs lettres. Ainsi le deux expressions suivantes, determinant et resultante, devront etre regardees comme synonymes.

(Smith vol. 2, page 477; Julio González Cabillón.)

Binet used the term RESULTANT in a memoir presented on the same occasion.

For the word in English the earliest citation in the OED is Cayley “On the Theory of Determinants,” 1843 reprinted in Papers vol. 1, p.63.

A list of matrix and linear algebra terms having entries on this web site is here.

DEVIANCE. The term was introduced by J. A. Nelder & R. W. M. Wedderburn in their fundamental paper on GENERALIZED LINEAR MODELS, viz. "Generalized Linear Models," Journal of the Royal Statistical Society, A, 135, (1972), 370-384. They write, "The fitting of the parameters at each stage is done by maximizing the likelihood for the current model and the matching of the model will be measured quantitatively by the quantity -2L_max which we propose to call the deviance." (p. 375) (David (1998))

DIAGONAL. Julio González Cabillón says, "Heron of Alexandria is probably the first geometer to define the term diagonal (as the straight line drawn from angle to angle)."

DIALYTIC was used by James Joseph Sylvester (1814-1897) in 1853 in Phil. Trans. CXLIII. i. 544:

Dialytic. If there be a system of functions containing in each term different combinations of the powers of the variables in number equal to the number of the functions, a resultant may be formed from these functions, by, as it were, dissolving the relations which connect together the different combinations of the powers of the variables, and treating them as simple independent quantities linearly involved in the functions. The resultant so formed is called the Dialytic Resultant of the functions supposed; and any method by which the elimination between two or more equations can be made to depend on the formation of such a resultant is called a dialytic method of elimination.

DIAMETER. According to Smith (vol. 2, page 278), “Euclid used the word ‘diameter’ in relation to the line bisecting a circle and also to mean the diagonal of a square, the latter term being also found in the works of Heron." The first reference is to Euclid Book 1, definition 17 and the second to proposition 34.

Euclid’s word diametros (according to Schwartzman composed of “across” and “measure”) was adopted into Latin. The English word appears in 1387 in John de Trevisa’s translation of Bartholomaeus Anglicus De Proprietatibus Rerum, “þe dyameter [of] a figure [is] þe lengest even lyne þat is devysed þerynne, take who þat may.” Robert Recorde’s Pathway to Knowledge of 1551 has “Def., And all the lines that bee drawen crosse the circle, and goe by the centre, are named diameters.” (OED).

See RADIUS.

DIFFERENTIAL CALCULUS, DERIVATIVE. The differential calculus required new terms when it was invented more than 300 years ago and it has gone on inspiring new terms ever since. Of course not all the terms that were coined remain in use, e.g. Newton’s term fluxion has not survived; see the entry FLUENT and FLUXION. See also Earliest Use of Symbols of Calculus.

Many of the basic terms were introduced by Gottfried Wilhelm Leibniz (1646-1716) writing in Latin. Because of the strength of the Newtonian tradition in England many of these terms entered English only in the 18^th or 19^th centuries.

DIFFERENTIAL CALCULUS. The term calculus differentialis was introduced by Leibniz in 1684 in Acta Eruditorum 3. Before introducing this term, he used the expression methodus tangentium directa (Struik, page 271). The OED has a nice quotation from Joseph Raphson’s Mathematical Dictionary of 1702: “A different way....passes....in France under the Name of Leibnitz’s Differential Calculus, or Calculus of Differences.” See also the entry CALCULUS.

DIFFERENTIAL EQUATION. Leibniz used the Latin aequationes differentiales in Acta Eruditorum, October 1684. See the entry ALGORITHM for the context.

Differential equation is found in English in 1704 in A Treatise on Fluxions by Charles Hayes: “We have this Differential Equation..which expresses the Nature of the Curve requir’d.” [OED]

DIFFERENTIAL (noun) appears in the title of a manuscript of Sept. 10, 1690, by Leibniz, “Methodus pro differentialibus, ponendo z = dy:dx et quaerendo dz ["A method for differentials, positing z = dy/dx and seeking dz”]. He may have used the term earlier, since he used the terms “differential equation” and “differential calculus” earlier.

Differential appears in English as a noun in 1704 in Lexicon technicum, or an universal English dictionary of arts and sciences by John Harris [OED].

For the modern interpretation see the entry FRÉCHET DIFFERENTIAL.

Leibniz’s immediate successors, the Bernoullis and Euler, also wrote in Latin but by the middle of the 18^th century French was becoming a major mathematical language. In modern English, when we speak of obtaining the derivative of a function by the process of differentiation, we are combining Lagrange’s French and Leibniz’s Latin.

DERIVATIVE. Joseph Louis Lagrange (1736-1813) used derivée de la fonction and fonction derivée de la fonction as early as 1772 in “Sur une nouvelle espece de calcul relatif a la différentiation et a l'integration des quantités variables,” Nouveaux Memoires de l'Academie royale des Sciences etBelles-Lettres de Berlin. (Oeuvres, Vol. III) pp. 441-478. Lagrange states, for instance (first pages):

...on designe de même par u'' une fonction derivée de u' de la même maniére que u' l'est de u, et par u''' une fonction derivée de même de u'' et ainsi, ...

... les fonctions u, u', u'', u''', u^IV, ... derivent l'une de l'autre par une même loi de sorte qu'on pourra les trouver aisement par une meme operation répetée. [the functions u, u', u'', u''', u^IV, ... are derived one another from the same law, such that ...]

Lagrange used these terms in his Théorie des fonctions analytiques (1797). He introduced the cognate term primitive: see the entry PRIMITIVE.

Not all French authors followed Lagrange. Sylvestre-François Lacroix (1765-1843) used the term coefficien différential in his Traité du calcul différentiel et integral p. 98 (Cajori 1919, page 272).

Lacroix’s book had a significant place in the history of mathematics in England for it was the first Continental calculus book to be translated. In 1816 it was translated by members of the Analytical Society, Babbage, Herschel and Peacock. DIFFERENTIAL COEFFICIENT appears in the translation: the OED quotes the passage: “The limit of the ratio of the increments, or the differential coefficient, will be obtained” [OED].The word DIFFERENTIATE also appears: “The differential coefficient being a new function....may itself be differentiated.” (OED).

The term DERIVATIVE (from Lagrange) made occasional appearances in English texts of the 19^th century: in 1834 W. R. Hamilton referred to the “derivative or differential coefficient” in his On a General Method in Dynamics Philosophical Transactions of the Royal Society. But it was not the favoured term. In his Differential and Integral Calculus (1891) George A. Osborne used the term differential coefficient but acknowledged, “The differential coefficient is sometimes called the derivative.” In the 20^th century the preference has been reversed: see G. H. Hardy A Course of Pure Mathematics (1908, p. 197).

In the 19^th and 20^th centuries new subjects with new constructions appeared. Besides those below see ABSOLUTE DIFFERENTIAL CALCULUS or TENSOR ANALYSIS.

According to Kline (p. 554), the term DIFFERENTIAL GEOMETRY was first used by Luigi Bianchi (1856-1928) in 1894; his 1894 book Lezioni di geometria differenziale had existed in a preliminary form since 1886. A major influence on Bianchi’s conception of the subject was Gauss’s work on surfaces (ca. 1825): see the entry GAUSSIAN CURVATURE. Kline’s account of the history of differential geometry begins in the 17th century with Huygens.

According to an announcement in the American Mathematical Monthly, 6, (1899), p. 158, Clark University was offering a course in differential geometry in 1899-1900. (JSTOR)

DIFFERENTIAL FORM. Victor J. Katz writes, “The mathematician chiefly responsible for clarifying the idea of a differential form was Elie Cartan. In his fundamental paper “Sur certaines expressions différentielles et le problème de Pfaff,” Annales Scientifiques de l'École Normale Supérieure (3) tome 16 (1899) 239-332, Cartan defines an “expression différentielle” as a symbolic expression given by a finite number of sums and products of the n differentials, and certain coefficient functions of the variables x_1, x_2, , …, x_n.” Katz adds that Cartan first used the terms “exterior differential form” and “exterior derivative” in his Leçons sur les invariants intégraux 1922. (Katz “The History of Stokes’ Theorem,” Mathematics Magazine, 52, (1979), 146-156.)

The term DIFFERENTIAL TOPOLOGY appears in Marston Morse’s “Closed Extremals,” Annals of Mathematics, 32, (1931), pp. 549-566 but, to judge from JSTOR, the term was not widely used before the 1960s. Differential topology first appears as a major category in Mathematical Reviews (one of 95) in 1961.

See TOPOLOGY.

DIFFERENTIABLE MANIFOLD. The term was introduced by Hassler Whitney "Differentiable Manifolds," Annals of Mathematics, 37, (1936), 645-680. Whitney remarks that "differentiable manifolds have been studied, for instance, by Oswald Veblen and J. H. C. Whitehead The Foundations of Differential Geometry ... 1932." However, neither the term nor the precise construction appears there.

DIFFEOMORPHISM appears in John Milnor “On Manifolds Homeomorphic to the 7-Sphere,” Annals of Mathematics, 64, (1956), pp. 399-405 with the explanation “A diffeomorphism f is a homeomorphism onto, such that both f and f ^-1are differentiable.” (p. 401, fn 3.) (JSTOR search)

See HOMEOMORPHISM.

For a list of entries associated with calculus see here.

DIGIT. According to Smith (vol. 2, page 12), the late Roman writers seem to have divided the numbers below 100 into digiti (fingers), articuli (joints), and compositi (composites of fingers and joints).

In English, Robert Recorde in the 1558 edition of the Ground of Artes wrote, "A diget is any numbre vnder 10."

The term DIGITADDITION was coined by D. R. Kaprekar, according to an Internet web page.

DIGRAPH was used in 1955 by F. Harary in Transactions of the American Mathematical Society. The term directed graph also occurs there [OED].

DIHEDRAL appears in 1799 in George Smith, The laboratory: or school of arts: "Terminating in dihedral pyramids" [OED].

DIHEDRAL ANGLE appears in 1826 in Henry, Elem. Chem.: "Variations of temperature produce a ... difference in ... a crystal of carbonate of lime.... As the temperature increases, the obtuse dihedral angles diminish ...so that its form approaches that of a cube" [OED].

DIOPHANTINE ALGEBRA is found in English in 1752 in The Elements of Algebra in a New and Easy method; Second Edition By Nathaniel Hammond: “In this Piece [referring to a German Algebra treatise] there are a great many curious Things relating especially to Diophantine Algebra.” [Google print search by James A. Landau].

DIOPHANTINE ANALYSIS (named for Diophantus of Alexandria) occurs in French in a letter of March 1770 from Euler to Lagrange: “ce problème me paraissait d'une nature singulière et surpassait même les règles connues de l'analyse de Diophante” (“this problem appeared to me to be of a singular nature and surpassed the known rules of Diophantine analysis”).

Lagrange used “analyse de Diophante” in a letter to D’Alembert in June 1771.

Diophantine analysis is found in English 1795 in A Mathematical and Philosophical Dictionary [Google print search].

[This entry was contributed by James A. Landau.]

DIOPHANTINE EQUATION. Felix Klein used Diophantische Gleichungen in “Die Eindeutigen automorphen Formen vom Geschlechte Null” in the 1892 issue of Nachrichten (page 286): “Die Relationen kann man in Diophantische Gleichungen umsetzen, welche dann leicht übersehen lassen, unter welchen Umständen Multiplicatorsysteme möglich sind, und in welcher Anzahl.” [James A. Landau]

Diophantine equation appears in English in 1893 in Eliakim Hastings Moore (1862-1932), "A Doubly-Infinite System of Simple Groups," Bulletin of the New York Mathematical Society, vol. III, pp. 73-78, October 13, 1893 [Julio González Cabillón].

Henry B. Fine writes in The Number System of Algebra (1902):

The designation "Diophantine equations," commonly applied to indeterminate equations of the first degree when investigated for integral solutions, is a striking misnomer. Diophantus nowhere considers such equations, and, on the other hand, allows fractional solutions of indeterminate equations of the second degree.

DIOPHANTINE PROBLEM. The phrase "Diophantus Problemes" appears in 1670 [James A. Landau].

The OED2 has the citation in 1700: Gregory, Collect. (Oxf. Hist. Soc.) I. 321: "The resolution of the indetermined arithmetical or Diophantine problems."

(DIRAC) δ FUNCTION. Paul Dirac introduced this "improper" function, as he called it, in his book The Principles of Quantum Mechanics (1930). After defining it, Dirac wrote "δ(x) is not a function of x according to the usual mathematical definition of a function, ... , but is something more general which we may call an 'improper function' to show its difference from a function defined by the usual definition. ... [Although] an improper function does not itself have a well-defined value, when it occurs as a function in an integrand the integral has a well-defined value." See the entry DISTRIBUTION and the article Delta-function. [John Aldrich]

DIRECT VARIATION. Directly is found in English in Sir Isaac Newton’s Mathematick Hilosophy [sic] More easily Demonstrated by William Whiston: “If a Body be mov’d in an Ellipsis about the Center off the same, the Centripetal Force will be directly as the Distance of the Body from the same Center.” [Google print search by James A. Landau]

Directly proportional is found in 1720 in Trigonometry Impro’d, and Projection of the Sphere Made Easy by Henry Wilson: “The Sines of the Angles subtended by the Perpendiculars, are directly proportional to the Sines of the Perpendiculars subtending.” [Google print search by James A. Landau]

Direct variation is found in 1839 in Introduction to the Literature of Europe in the Fifteenth, Sixteenth, and Seventeenth Centuries by Henry Hallam [Google print search].

The term DIRECTION COEFFICIENT (for cos x + i sin x) is due to Hankel (1867) (Smith, 1906).

Direction coefficient is found in English in a 1902 reprint, 1896 copyright, of a translation of the fourth German edition of Elements of the Theory of Functions of a Complex Variable by H. Durège. The first edition of Durège’s work appeared in 1864 and the second edition in 1873 and the title was Theorie der Functionen. [Google print search by James A. Landau]

Argand used the term direction factor (Smith, 1906).

Cauchy used the term reduced form (l'expression réduite) (Smith, 1906).

DIRECTION FIELD is found in the context of an alternating current through a coil in 1900 in The Builder [Google print search by James A. Landau].

Direction field is found in 1910 in "The Theorem of Thomson and Tait and Natural Families of Trajectories" by Edward Kasner in Transactions of the American Mathematical Society, Vol. 11, No. 2 (Apr., 1910), pp. 121-140. [JSTOR serach]

See SLOPE FIELD.

DIRECTIONAL DERIVATIVE is found in 1899 in A Short Table of Integrals by B. O. Pierce: “The directional derivative of any scalar point function, u, at any point, P, in any fixed direction PQ’, is the limit, as PQ approaches zero, of the ratio of u_Q - u_P to PQ, where Q is a point on the straight line PQ’ between P and Q’. [Google print search by James A. Landau]

DIRECTRIX. According to the DSB, Jan de Witt (1625-1672) "is credited with introducing the term 'directrix' for the parabola, but it is clear from his derivation that he does not use the term for the fixed line of our focus-directrix definition."

DIRICHLET INTEGRAL AND DIRICHLET DISTRIBUTION. Several integrals are associated with Lejeune Dirichlet: see MathWorld: Dirichlet Integrals. One is associated with DIRICHLET’S PRINCIPLE. Another, considered here, is a multivariable extension of the BETA-FUNCTION, which was first presented in Dirichlet’s “Sur une nouvelle méthode pour la détermination des intégrales multiples,” Journal de mathématiques pures et appliquées (Liouville) 4 1839) 164-9. The associated probability distribution, a generalisation of the BETA-DISTRIBUTION, is given in W. G. Madow’s “Contributions to the Theory of Multivariate Statistical Analysis,” Transactions of the American Mathematical Society, 44, (1938), 454-495. (JSTOR search.) However, it seems that the distribution is much older and even predates Dirichlet: it appears in a Bayesian analysis in Laplace’s “Mémoire sur les probabilités,” Mémoires de l'Académie royale des sciences de Paris, 1778, pp. 227-332. For this and other appearances of the distribution, see R. D. Gupta, and D. St. Richards “The History of the Dirichlet and Liouville Distributions,” International Statistical Review, 69, (2001), 433-446. See also Wikipedia: Dirichlet distribution. [John Aldrich]

Dirichlet’s integral is found in English in 1851 in “On the index symble of homogeneous functions” by Robert Carmichael in The Cambridge and Dublin Mathematical Journal: “It will be seen that this result bears a strong resemblance to Liouville’s well-known extension of Dirichlet’s Integral.” [Google print search by James A. Landau]

DIRICHLET’S PRINCIPLE and PROBLEM. According to G. Birkhoff & E. Kreyszig “The Establishment of Functional Analysis,” Historia Mathematica, 11, p. 271 the problem which involves the solution of a certain partial differential equation had been posed by Gauss in 1840 and discussed by W. Thomson in 1847 around the time Dirichlet treated it in his lectures. Dirichlet’s contribution appeared as “Ueber einen neuen Ausdruck zur Bestimmung der Dichtigkeit einer unendlich dünnen Kugelschale, wenn der Werth des Potentials derselben in jedem Punkte ihrer Obertläche gegeben ist,” Abhandlungen der Königlich Preussischen Akademie der Wissenchaften von 1850, S. 99-116. See Werke 2 p. 69. Riemann introduced the term Dirichlet principle (Dirichlet’sches Princip) for the method of solving the problem by finding the function that minimises a certain integral and which Dirichlet had described in his lectures: see Riemann’s “Grundlagen für eine allgemeine Theorie der Funktionen einer veränderlichen komplexen Grösse” (1851) in Werke 1 p. 47. See the Encyclopaedia of Mathematics entries Dirichlet problem and Dirichlet principle.

The English expressions are found in 1893 in A Treatise on the Theory of Functions by James Harkness and Frank Morley where they write, none too accurately, “The basis for Riemann’s work is a famous proposition known among continental mathematicians as Dirichlet’s Principle, or Problem.”

DISCRETE appears in English in 1570 in Sir Henry Billingsley's translation of Euclid's Elements: "Two contrary kynds of quantity; quantity discrete or number, and quantity continual or magnitude" [OED].

DISCRETE MATHEMATICS. The Twelfth Annual Report of the Ohio State Academy of Science, April 15, 1904, has: “The new mathematics...has triumphed for its own domain in cases where the continuity methods were wholly inapplicable, where arithmology, discrete mathematics was called-for and victorious. ... The brilliant and rapid advances in chemistry have come not from suppressing but from stressing the individuality of the elements. Its mathematics has been essentially discrete.” [Google print search by James A. Landau]

In 1931 Science at the Cross Roads: Papers Presented to the International Congress of the History of Science and Technology has: “We are thus presented with two extremes: continuity transformed into the absolute and the discrete made absolute, both laying claim to independent and sole significance, neither seeking reciprocal unity, each giving a one-sided picture of material reality. Consequently, the problem is not solved by rejected both analysis and discrete mathematics....” [Google print search by James A. Landau]

In 1959 “Some Basic Mathematical Concepts,” School Mathematics Study Group has: “What is needed is a discrete mathematics to parallel and supplement our better known continuous mathematics.” [Google print search by James A. Landau]

Classified advertisements appear in 1960 in The New Scientist. It is a help-wanted ad from Sperry Rand Research Center saying there were openings in the Department of “Applied Mathematics & Theoretical Physics: Theoretical Physics; Information Theory; Discrete Mathematics; Random Processes.” No further context is available to explain what was meant by “discrete mathematics.” [Google print search by James A. Landau]

Discrete Mathematics occurs in 1971 in the title of the journal Discrete Mathematics. The fields covered include: graph and hypergraph theory, network theory, coding theory, block designs, lattice theory, the theory of partially ordered sets, combinatorial geometrics, matroid theory, extremal set theory, logic and automata, matrices, polyhedra, and discrete probability theory.

See FINITE MATHEMATICS.

DISCRIMINANT. An English translation of Geschichte der Elementar-Mathematik by Karl Fink has:

It was Sylvester also, who in 1851 introduced the name “discriminant” for the function which expresses the condition for the existence of two equal roots of an algebraic equation; up to this time, it was customary, after the example of Gauss, to say “determinant of the function.”

The citation is Sylvester J. J. (1851) “On a remarkable discovery in the theory of canonical forms and of hyperdeterminants,” Phil Mag, series 2, (1851), 391-410. [Dick Nickalls]

In 1876 George Salmon used discriminant in its modern sense in Mod. Higher Algebra (ed. 3): "The discriminant is equal to the product of the squares of all the differences of the differences of any two roots of the equation" [OED].

The term geometric discriminant is described in detail in Nickalls RWD and Dye RH (1996) The geometry of the discriminant of a polynomial, The Mathematical Gazette (1996), vol 80 (July), pp 279--285. The authors believe they are the first to define this geometric analog of the typical “algebraic” discriminant.

R. A. Fisher introduced and named the DISCRIMINANT FUNCTION, the principal tool of discriminant analysis, in "The Use of Multiple Measurements in Taxonomic Problems" Annals of Eugenics, 7: 179-188 (1936). The phrase DISCRIMINANT ANALYSIS appears in Fisher’s second paper on the subject "The Statistical Utilization of Multiple Measurements" Annals of Eugenics, 8 : 376-386 (1938). (David 2001)

DISJOINT is found in 1909 in C. J. Keyser "The Thesis of Modern Logistic," Science, New Series, 30, No. 783. (Dec. 31), p. 956: "two classes are disjoint if neither includes a term of the other." (JSTOR)

The converse, conjoint, was not applied to classes but it was used elsewhere: from George Ballard Mathews Projective Geometry (1914), "Taking any two elements of different names (plane, point; plane, line; point, line), we may distinguish them as being disjoint or conjoint (p. 3).

DISJUNCTION was considered by the Stoic logicians. W. & M. Kneale The Development of Logic (1962) pp. 160-1 state that when it came to interpretations of disjuction Chrysippus of Soli (280 BC - 206 BC) and his followers "seem to have assumed" that exclusive disjunction, i.e. that two alternatives could not be true together, "was the only proper one." For general information on the Stoics see Dick Baltzly Stoicism.

Disjunction and disjunctive came into English in the 16^th century, not in textbooks on logic, which continued to be written in Latin for another century, but in works for other audiences. The OED's earliest quotations come from Abraham Fraunce The Lawiers Logike, exemplifying the Praecepts of Logike by the Practise of the Common Lawe (1588) and from Dudley Fenner A Defence of the Godlie Ministers (1587), a book on church government. The word is traced to Old French and to Latin.

DISME is an obsolete English word meaning "tenth." It occurs in 1608 in the title Disme: The Art of Tenths, or Decimall Arithmetike. This work is a translation by Robert Norman of La Thiende, by Simon Stevin (1548-1620), which was published in Flemish and in French in 1585.

Disme was used by Shakespeare in Troilus and Cressida (ii, 2, 15), which was first published in 1609. The use of this word is one of the pieces of evidence cited by defenders of the theory that Shakespeare's plays were actually written someone else, perhaps Francis Bacon.

DISPERSION (in statistics) is found in 1876 in Catalogue of the Special Loan Collection of Scientific Apparatus at the South Kensington Museum by Francis Galton (David, 1998).

DISTRIBUTED LAG. The term was used by Irving Fisher in his 1925 paper "Our Unstable Dollar and the so-called Business Cycle" (Journal of the American Economic Association, 20, 179-202) to describe a formulation he had used in "The Business Cycle Largely a 'Dance of the Dollar,'" Journal of the American Statistical Society, 18, (1923), 1024-1028 [John Aldrich].

See the entry LAG.

DISTRIBUTION in the sense of a generalized function was introduced by Laurent Schwartz in his paper Généralisation de la notion de fonction, de dérivation, de transformation de Fourier et applications mathématiques et physiques (1945). This presented a theory of distributions in which such "improper functions" as the DIRAC δ FUNCTION could be treated rigorously.

DISTRIBUTION FUNCTION. A Google search by James A. Landau finds Verteilungsfunktion in an 1890 book written in Swedish.

Verteilungsfunktion is found in R. von Mises "Grundlagen der Wahrscheinlichkeitsrechnung," Math. Zeit. 5, (1919), 52-99.

Distribution function is found in English in the 1902 Encyclopaedia Britannica, but in combinatorial analysis, not statistics. [Google print search, James A. Landau]

Distribution function apparently is used in the May 1933 paper by Victor Perlo, “On the Distribution of Student's Ratio for Samples of Three Drawn from a Rectangular Distribution,” Biometrika, vol. 25, no. 1/2. [Google print search, James A. Landau]

The term cumulative distribution function was used by S. S. Wilks Mathematical Statistics (1943) (David 2001).

(See also Symbols in Probability on the Symbols in Probability and Statistics page.)

DISTRIBUTIVE. See commutative.

The term DIVERGENCE (of a vector field) was introduced by William Kingdon Clifford (1845-1879) in his book Elements of Dynamic (1878). It was the negative of the quantity James Clerk Maxwell had called the convergence. Maxwell suggested this term in 1870 in a letter to Tait, reproduced in the entry CURL. It was proposed more formally in Maxwell’s "On the Mathematical Classification of Physical Quantities," Proceedings of the London Mathematical Society, 3, (1871), 257-266.  Maxwell gave a fuller account of the term in the section, Effect of Hamilton’s operation 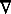on a vector function, of his A Treatise on Electricity and Magnetism (1873, p. 27)

Oliver Heaviside started using the term divergence in 1883 and he may have come up with the term independently of Clifford.

See also QUATERNION and VECTOR ANALYSIS for related terms and Vector Calculus Symbols on the the Earliest Uses of Symbols of Calculus page.

[Based on M. J. Crowe A History of Vector Analysis (2^nd edition, pp. 131-2, 165-6)]

DIVERGENCE THEOREM or GAUSS'S THEOREM. A JSTOR search found Gauss’s theorem in Henry A. Rowland “On the Motion of a Perfect Incompressible Fluid When no Solid Bodies are Present,” American Journal of Mathematics, 3, (1880), pp. 226-268 and divergence theorem in Oliver Heaviside “On the Forces, Stresses, and Fluxes of Energy in the Electromagnetic Field,” Philosophical Transactions of the Royal Society A, 183 (1892), 423-480. It seems likely however that both terms were already established.

The history of the theorem is bewildering with many re-discoveries.

O. D. Kellogg Foundations of Potential Theory (1929, p. 38) has the following note on the result “known as the Divergence Theorem, or as Gauss’ Theorem or Green’s Theorem”:

A similar reduction of triple integrals to double integrals was employed by Lagrange: Nouvelles recherches sur la nature et la propagation du son Miscellanea Taurinensis, t. II, 1760-61; Oeuvres t. I, p. 263. The double integrals are given in more definite form by Gauss Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodo novo tractate, Commentationes societas scientiarum Gottingensis recentiores, Vol III, 1813, Werke Bd. V pp. 5-7. A systematic use of integral identities equivalent to the divergence theorem was made by George Green in his Essay on the Mathematical Theory of Electricity and Magnetism; Nottingham, 1828 [Green Papers, pp. 1-115].

Kline (pp. 789-90) writes that Mikhail Ostrogradski obtained the theorem when solving the partial differential equation of heat. He published the result in 1831 in Mem. Ac. Sci. St. Peters., 6, (1831) p. 39. J. C. Maxwell had made the same attribution in the 2^nd edition of the Treatise on Electricity and Magnetism (1881).  See also the Encyclopaedia of Mathematics entry Ostrogradski formula

For Gauss’s theorem Hermann Rothe “Systeme Geometrischen Analyse, Erster Teil” Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen   Volume: 3, T.1, H.2 p. 1345 refers to Gauss’s Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstossung-Kräfte 1839 in Werke Bd. V (especially pp. 226-8.)

[This entry was contributed by John Aldrich, and was based on M. J. Crowe A History of Vector Analysis (2^nd edition, pp. 146-7)]

DIVERGENT. See convergent.

DIVIDEND. Joannes de Muris (c. 1350) used dividendus (Smith vol. 2, page 131).

In English, the word is found in The Grovnd of Artes, by Robert Recorde, which was printed between 1540 and 1542: "Then begynne I at the hyghest lyne of the diuident, and seke how often I may haue the diuisor therin" [OED].

The term DIVINE PROPORTION appears in 1509 in the title De Divina Proportione by Luca Pacioli (1445-1517). According to an Internet website, Pacioli coined the term.

Ramus wrote, "Christianis quibusdam divina quaedam proportio hic animadversa est..." in Scholarvm Mathematicarvm, Libri vnvs et triginta, Basel, 1569; ibid., 1578; Frankfort, 1599) (Smith vol. 2, page 291).

Kepler wrote, "Inter continuas proportiones unum singulare genus est proportionis divinae" (Frisch ed. of his Opera, I (1858). According to v. Baravalle (1948), Kepler used the term sectio divina.

DIVISION is found in English in "The crafte of nombrynge" (ca. 1300). The word is spelled dyuision [OED].

Baker (1568) speaks of "Deuision or partition" and Digges (1572) says "To deuide or parte" (Smith vol. 2, page 129).

DIVISOR is found in English in "The crafte of nombrynge" (ca. 1300). The word is spelled dyvyser [OED].

DODECAGON is found in English in a mathematical dictionary of 1658.

DOMAIN was used in 1886 by Arthur Cayley in "On Linear Differential Equations" in the Quarterly Journal of Pure and Applied Mathematics: “... for points x within the domain of the point a” [University of Michigan Historic Math Collection].

Domain is found in 1896 in Bull. Amer. Math. Soc. Dec. 103: "The formation of an algebraic ‘domain’ and..the nature of the process of ‘adjunction’ introduced by Galois" [OED].

Domain, referring to a power series, appears in 1898 in Introduction to the theory of analytic functions by J. Harkness and F. Morley.

Domain, in the sense of the values that an independent variable of a function can take, appears in the Encyclopaedia Britannica of 1902 [OED].

In 1909 Webster’s New International Dictionary, Unabridged includes in the definition of domain: “Any region, extent, or aggregate, geometrical or arithmetical, of points, values, or other elements, to which a variable is confined and anywhere within which it may be.”

In 1914 A. R. Forsyth, Theory of Functions of Two Complex Variables iii. 57, has: “A restricted portion of a field of variation is called a domain, the range of a domain being usually indicated by analytical relations” [OED].

DOMAIN OF RATIONALITY is a translation of Kronecker’s term Rationalitätsbereich.

DOMINANCE (in game theory and decision theory). The term "dominates" is prominent in J. von Neumann and O. Morgenstern Theory of Games and Economic Behavior (1944). L. J. Savage Foundations of Statistics (1954) used the term in statistical decision theory. Wald, the founder of that theory, had used "absolutely better than," e.g. in his "Contributions to the Theory of Statistical Estimation and Testing Hypotheses," Annals of Mathematical Statistics, 10, (1939), 299-326.

DOPPELVERHÄLTNISS. Möbius introduced the term Doppelschnittverhältniss, meaning "ratio bisectionalis" or "double cut ratio," in his "Der barycentrische Calcul" (1827): gesammelte Werke, I (1885).

Jakob Steiner shortened the term to Doppelverhältniss (Smith vol. 2, page 334).

See also anharmonic ratio and cross-ratio.

DOT PRODUCT is found in 1901 in Vector Analysis by J. Willard Gibbs and Edwin Bidwell Wilson:

The direct product is denoted by writing the two vectors with a dot between them as

A·B

This is read A dot B and therefore may often be called the dot product instead of the direct product.

DOUBLE INTEGRAL appears in the title of Adrien-Marie Legendre, “Mémoire sur les Intégrales Doubles,” Paris, Mem. Acad. Sc. for 1788, published 1791, pp. 454-486. [James A. Landau]

Both double integral and triple integral occur in English in Philosophical Transactions of the Royal Society of London for the year MDCCCI, “Demonstration of a Theorem, by which such Portions of the Solidity of a Sphere are assigned as admit an algebraic Expression” by Robert Woodhouse, read February 12, 1801. [Google print search, James A. Landau]

DUALITY. The term "principle of duality" was introduced by Joseph Diaz Geronne (1771-1859) in "Considérations philosophiques sur les élémens de la science de l'étendue," Annales 16 (1825-1826) (DSB).

The term DUMMY VARIABLE is often used when describing the status of a variable like x in a definite integral. A. Church seems to be describing an established usage when he wrote in 1942, "A variable is free in a given expression ... if the expression can be considered as representing a function with that variable as an argument. In the contrary case the variable is called a bound (or apparent or dummy) variable." ("Differentials", American Mathematical Monthly, 49, 390.) [John Aldrich].

In regression analysis a DUMMY VARIABLE indicates the presence (value 1) or absence of an attribute (0).

A JSTOR search found "dummy variables" for social class and for region in H. S. Houthakker's "The Econometrics of Family Budgets" Journal of the Royal Statistical Society A, 115, (1952), 1-28.

A 1957 article by D. B. Suits, "Use of Dummy Variables in Regression Equations" Journal of the American Statistical Association, 52, 548-551, consolidated both the device and the name.

Kendall & Buckland in their Dictionary of Statistical Terms object: the term is "used, rather laxly, to denote an artificial variable expressing qualitative characteristics .... [The] word ‘dummy’ should be avoided." Apparently these variables were not dummy enough. For Kendall & Buckland a dummy variable signifies "a quantity written in a mathematical expression in the form of a variable although it represents a constant", e.g. when the constant in the regression equation is represented as a coefficient times a variable that is always unity.

The indicator device, without the name "dummy variable" or any other, was also used by writers on experiments who put the analysis of variance into the format of the general linear hypothesis, e.g. O. Kempthorne in his Design and Analysis of Experiments (1952) [John Aldrich].

DUODECIMAL is dated 1663 in MWCD10.

Duodecimal appears in 1714 in the title A new and complete Treatise of the Doctrine of Fractions .. with an Epitome of Duodecimals by Samuel Cunn [OED].

DURBIN-WATSON TEST. The test and associated distribution theory were given by J. Durbin; G. S. Watson "Testing for Serial Correlation in Least Squares Regression," Parts I and II, Biometrika, 1950-1. In an ET interview Durbin described the background to the work.

DUTCH BOOK (ARGUMENT) in subjective probability theory. The term entered circulation in the 1950s. R. Sherman Lehman explains the term, "If a bettor is quite foolish in the choice of the rates at which he will bet, an opponent can win money from him no matter what happens. The phenomenon is well known to professional bettors--especially bookmakers ... Such a losing book is known by them as a ‘dutch book.’ Our investigations are thus concerned with necessary and sufficient conditions that a book not be ‘dutch.’" ("On Confirmation and Rational Betting," Journal of Symbolic Logic, 20, (1955), p. 251.)

The classic use of the Dutch book argument to obtain the properties of subjective odds is B. De Finetti’s "La prévision: ses lois logiques, ses sources subjectives," Annales de l'Institute Henri Poincaré, 7, (1937) 1-68. The term "Dutch book," however, is not used.

DYAD. The Greek word dyad is found in Euclid in Proposition 36 of Book IX and in Nichomachus’ Introduction to Arithmetic (Book I, Chapter VII) [Mary Townsend].

The term was used in chemistry in the 19th century, referring to an element of valence 2, such as oxygen. The term is used in crystallography in 1899. [Google print searches, James A. Landau]

In the sense of a mathematical operator, dyad was used in 1884 by Josiah Willard Gibbs (1839-1903) in his Elements of Vector Analysis.