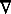Earliest Known Uses of Some of the Words of Mathematics (L)

Last revision: March 2, 2020

LAGRANGE MULTIPLIER. Joseph-Louis Lagrange states the general principle for maximising a function of n variables when there are one or more equations between the variables in his Théorie des Fonctions Analytiques (1797, p. 198): "il suffira d'ajouter à la function proposée les functions qui doivent être nulles, multipliées chacune par une quantité indéterminée ...". Lagrange originally applied the multiplier technique to problems in the calculus of variations in his Mécanique Analytique (1788, pp. 46-7). (See H. H. Goldstine A History of the Calculus of Variations from the 17^th through the 19^th Century (1980).)

Although "Lagrange multiplier" is the standard term today, "undetermined multiplier" and "indeterminate multiplier" were the usual terms in the 19^th century and for much of the 20^th.

Lagrange’s method of multipliers is found in 1845 in the title “On the Theory and Application of Lagrange’s Method of Multipliers” by William Rutherford, in The Mathematician, editors Thomas Stephens Davies, William Rutherford, and Stephen Fenwick. [Google print search by James A. Landau]

The term "Lagrange’s method of undetermined multipliers" appears in J. W. Mellor, Higher Mathematics for Students of Chemistry and Physics (1912) [James A. Landau].

The term "Lagrange multiplier rule" appears in "The Problem of Mayer with Variable End Points," Gilbert Ames Bliss, Transactions of the American Mathematical Society, Vol. 19, No. 3. (Jul., 1918).

Lagrange multiplier is found in "Necessary Conditions in the Problems of Mayer in the Calculus of Variations," Gillie A. Larew, Transactions of the American Mathematical Society, Vol. 20, No. 1. (Jan., 1919): "The [lambda]’s appearing in this sum are the functions of x sometimes called Lagrange multipliers."

The use of Lagrangian for the augmented function dates from the 1960s, see e.g. Samuel Zahl "A Deformation Method for Quadratic Programming," Journal of the Royal Statistical Society, B, 26, (1964), p. 153. (JSTOR search) The Lagrangian function or the Lagrangian expression were once the popular terms.

LAGRANGE MULTIPLIER TEST in Statistics. This test principle was introduced by S. D. Silvey "The Lagrangian Multiplier Test," Annals of Mathematical Statistics, 30, (1959), 389-407. However, while Silvey’s derivation was new, the test statistic was already in the literature as the "score test." Econometricians tend to favour the Lagrange term and statisticians the score term.

See the entries SCORE TEST and WALD TEST.

LAGRANGE’S THEOREM. Formule de Lagrange appears in Traité élémentaire de calcul différentiel et de calcul intégral (1797-1800) by Lacroix.

Lagrange’s theorem appears in 1818 in An Elementary Treatise on Physical Astronomy by Robert Woodhouse: “we require a formula assigning v in terms of nt. Such a formula we may deduce from Lagrange’s Theorem.” [Google print search by James A. Landau]

Lagrange’s theorem appears in An Elementary Treatise on Curves, Functions and Forms (1846) by Benjamin Peirce: "The theorem (650) under this form of application, has been often called Laplace’s Theorem; but, regarding this change as obvious and insignificant, we do not hesitate to discard the latter name, and give the whole honor of the theorem to its true author, Lagrange."

Lagrange’s formula for interpolation appears in 1849 in An Introduction to the Differential and Integral Calculus, 2nd ed., by James Thomson.

Lagrange’s method of approximation occurs in the third edition of An Elementary Treatise on the Theory of Equations (1875) by Isaac Todhunter.

LAGRANGIAN FUNCTION is found in 1877 in E. J. Routh, A Treatise on the Stability of a Given State of Motion, Particularly Steady Motion. [Google print search by James A. Landau]

LAGRANGIAN (as a noun) occurs in Th. Muir, "Note on the Lagrangian of a special unit determinant," Transactions Royal Soc. South Africa (1929).

LAPLACE’S COEFFICIENTS. According to Todhunter (1873), "the name Laplace’s coefficients appears to have been first used" by William Whewell (1794-1866) [Chris Linton].

Laplace’s coefficients appears in 1830 in the Encyclopædia Metropolitana, 2nd ed. [Google print search by James A. Landau]

LAPLACE’S EQUATION appears in 1812 in Philosophical Transactions of the Royal Society of London for the year MDCCCXII Part I. [Google print search by James A. Landau]

The LAPLACE EXPANSION of a determinant is generally traced to Laplace’s memoir in Histoire de l'Académie royale des sciences 1776 (Année 1772, 2e partie) pp. 267-376 (see pp. 294-304). Thomas Muir makes a detailed examination of the argument in The Theory of Determinants in the Historical Order of Development vol. 1, pp. 24-33: he concludes, “there can be no doubt that if any one name is to be attached to the theorem it should be that of Laplace.” [John Aldrich]

Laplace’s expansion-theorem is found in Proceedings of the Royal Society of Edinburgh Volume VIII November 1872 to July 1875, in a paper read on Jan. 5, 1874. [Google print search by James A. Landau]

LAPLACE’S FUNCTIONS appears in English in 1833 in Elementary principles of the theories of electricity, heat and molecular actions by Robert Murphy. [Google print search]

The term LAPLACE’S OPERATOR (for the differential operator 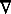²) was used in 1873 by James Clerk Maxwell in A Treatise on Electricity and Magnetism (p. 29): "...an operator occurring in all parts of Physics, which we may refer to as Laplace’s Operator" (OED).

See VECTOR ANALYSIS and the Earliest Uses of Symbols of Calculus page

The term LAPLACE TRANSFORM was used by Boole and Poincaré. According to the website of the University of St. Andrews, Boole and Poincaré might otherwise have used the term Petzval transform but they were influenced by a student of Józeph Miksa Petzval (1807-1891) who, after a falling out with his instructor, claimed incorrectly that Petzval had plagiarised Laplace’s work.

LAPLACIAN is found in 1889 in A Treatise on Statics with Applications to Physics Vol. II, 4th ed., by George Minchin. The preface (which is dated February, 1886) has on page vi:

In this Chapter I have also ventured to introduce the term “Laplacian” with reference to those remarkable coefficients which occur in the development of the reciprocal of the distance between two points. The general term “Spherical Harmonic” is, of course, retained; but it seems to me that the name of Laplace ought to be explicitly connected with the branch of Mathematical Physics which he did so much to develop, and which has now become of such great importance. The pure mathematicians having their “jacobians,” “Hessians,” “Cayleyans,” &c., the term “Laplacian” is surely justified.

[Google print search by James A. Landau]

LAPLACIAN (as a noun, for the differential operator 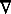²) was used in 1935 by Pauling and Wilson in Introd. Quantum Mech. (OED).

See VECTOR ANALYSIS.

LATENT VALUE and VECTOR. See EIGENVALUE.

The term LATIN SQUARE was named by Euler (as quarré latin) in 1782 in "Recherches sur une Nouvelle Espèces de Quarrés Magique," Verh. uitgegeven door het Zeeuwsch Genootschap d. Wetensch. te Vlissingen, 9, 85-232.

Latin square appears in English in 1890 in the title of a paper by Arthur Cayley, "On Latin Squares" in Messenger of Mathematics. Graeco-Latin square appears in H. F. MacNeish "Euler Squares." Ann. Math. 23, (1921-1922), 221-227.

Graeco-Latin square appears in 1898 in “A New Method in Combinatory Analysis, with application to Latin Squares and associated questions,” by Major P. A. MacMahon, in Transactions of the Cambridge Philosophical Society Volume XVI. [Google print search by James A. Landau]

The term was introduced into statistics by R. A. Fisher, according to Tankard (p. 112). Fisher used the term in 1925 in Statistical Methods for Research Workers p. 229 (OED).

See the entry EULER’s GRAECO-LATIN SQUARES CONJECTURE.

LATITUDE and LONGITUDE. Henry of Ghent used the word latitudo in connection with the concept of latitude of forms.

Nicole Oresme (1320-1382) used the terms latitude and longitude approximately in the sense of abscissa and ordinate.

LATTICE and LATTICE THEORY are found in 1899 in “Memoir on the Theory of the Partitions of Numbers” by Major Percy Alexander MacMahon, Philosophical Transactions of the Royal Society of London Series A Vol. 192: “There is also a lattice theory connected with unipartite partitions on a line, for the unit-graph of such a partition is nothing more than a number of units and zeros placed at the points of a two-dimensional lattice....” [Google print search by James A. Landau]

LATTICE and LATTICE THEORY in algebra. These terms were introduced by Garrett Birkhoff in his “On the combination of subalgebras,” Proceedings of the Cambridge Philosophical Society, 29, (1933), 441–464 and became well-known through his book Lattice Theory (1940). See Enyclopedia of Mathematics where earlier work by Schröder and Dedekind and contemporary work by Ore are also described.

Man stele sich jetzt in der Ebene ein rechtwinkliges Coordinatesystem (x, y) und die ganze Ebene durch Parallelen mit den Axen in den Abständen = 1 von einander in lauter Quadrate von den Dimensionen = 1 getheilt vor. Gitterpuncte sollen alle Eckpuncte von Quadraten heifsen, welche nicht in den beiden Coordinaten – Axen liegen.

The term Gitterpuncte may well have been used earlier.

The earliest use of lattice point in English given by the OED is from Cayley’s translation of Eistenstein, which is titled “Eisenstein’s Geometrical Proof of the Fundamental Theorem for Quadratic Residues” and appears in the Quarterly Mathematical Journal, vol. I. (1857), pp. 186-191: “Imagine now in a plane, a rectangular system of coordinates (x, y) and the whole plane divided by lines parallel to the axes at distances = 1 from each other into squares of the dimension = 1. And let the angles which do not lie on the axes of coordinates be called lattice points.”

[James A. Landau]

The term LATUS RECTUM was used by Gilles Personne de Roberval (1602-1675) in his lectures on Conic Sections. The lectures were printed posthumously under the title Propositum locum geometricum ad aequationem analyticam revocare,... in 1693 [Barnabas Hughes].

Latus rectum is found in English in A Mathematical Dictionary by Joseph Raphson: “In a Parabola the Rectangle of the Diameter, and Latus Rectum, is equal to the Rectangle of the Segments of the double Ordinate.” [OED]

LAURENT EXPANSION. Pierre-Alphonse Laurent announced this result in his "Extension du théorème de M. Cauchy relatif à la convergence du développement d'une fonction suivant les puissances ascendantes de la variable," Comptes rendus, 17, (1843) pp. 348-9. The full paper was published in Journal de l’Ecole Polytechnique. 23, (1863), 75-204. (Kline p. 641)

The term LAW OF INTERTIA OF QUADRATIC FORMS was introduced by James Joseph Sylvester in his “A demonstration of the theorem that every homogeneous quadratic polynomial is reducible by real orthogonal substitutions to the form of a sum of positive and negative squares,” Philosophical Magazine, 4, 138-142. It is sometimes called Sylvester’s law of inertia. See Kline (p. 799) and the entry in Encyclopedia of Mathematics. [John Aldrich]

LAW OF LARGE NUMBERS, STRONG LAW, WEAK LAW. La loi de grands nombres appears in 1835 in Siméon-Denis Poisson (1781-1840), "Recherches sur la Probabilité des Jugements, Principalement en Matiére Criminelle," Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences, 1, 473-494 also in his "La loi de grands nombres" in ibid. 2, (1836) 377-382. (Porter p. 77).

By Poisson’s time there were several theorems that could be covered by this phrase. The first, given by Jacob Bernoulli in Ars Conjectandi (1713), was about "Bernoulli trials" (a 20^th century term). It was often called "Bernoulli’s theorem": see e.g. Todhunter’s A History of the Mathematical Theory of Probability (1865, p. 71). In the course of the 19^th century analogous results were found for other types of random variable.

Law of large numbers is found in 1863 in “On the Military Statistics of the United States of America” by F. B. Elliot: “....may be expressed by a very simple analytical function (see Note in Appendix), first investigated by J. Bernoulli in its relation to the probable distribution of errors of observation of a single object; extended by Poisson, under the title the law of large numbers, to the measurement of many objects, representative each of a common type; and first applied by M. Quetelet to the physical measurement of men.” [Google print search by James A. Landau]

In the 20^th century a new kind of convergence result was obtained, based on almost-sure convergence, not convergence in probability, as in the Bernoulli tradition. The first of these results (on Bernoulli trials) was given by E. Borel in 1909 (see NORMAL NUMBER) and a more general result was given by F. Cantelli in 1917. In 1928 A. Y. Khintchine introduced the term strong law of large numbers to distinguish these results from the "ordinary" Bernoulli-like results: "Sur la loi forte des grands nombres," Comptes Rendus de l'Académie des Sciences, 186 page 286.

The obvious term for the Bernoulli results viz., the weak law of large numbers, seems to have come later. A JSTOR search (restricted to journals in English) produced W. Feller’s 1945 "Note on the Law of Large Numbers and "Fair" Games," Annals of Mathematical Statistics, 16, 301-304.

LAW OF QUADRATIC RECIPROCITY. Legendre used loi de réciprocite in 1808 in his Essai Sur La Théorie des Nombres; Seconde Édition: “Démonstration du Théorème contenant la loi de réciprocite qui existe entre deux nombres premiers quelconques.”

In English, law of quadratic reciprocity is found in Report of the annual meeting of the British Association for the Advancement of Science in the Sept. 1859 meeting, by H. J. Stephen Smith. [Google print search by James A. Landau].

LAW OF SINES (Snell’s law). In a letter to the editor of the Edinburgh Review dated Jan. 3, 1837, and printed in History of the Inductive Sciences from the earliest to the present times Volume the First by John W. Parker, William Whewell wrote, “This letter is a repetition of one written in October last, with an alteration of the paragraph respecting Sir C. Bell and Mr. Mayo. .... Most of the other corrections I reject. On the subject of the discovery of the law of the sines in refraction, his criticism is erroneous. Snell’s law is the law of sines; Descartes had seen Snell’s papers; and from Descartes’s habits of mind, I am persuaded that he did borrow the discovery thence.”

The law of sines is found in 1847 in A Text-Book on Natural Philosophy for the use of schools and colleges by John William Draper. The book more frequently has “law of the sines,” but “law of sines” appears as a page heading. Page 186 has “...the general law of refraction is as follows:--- In each medium the sine of the angle of incidence is in a constant ratio to the sine of the angle of refraction.... To a beginner, this law of the constancy of sines may be explained as follows:---....”

[Google print search by James A. Landau]

LAW OF SINES, LAW OF COSINES, LAW OF TANGENTS. The three terms are found in 1888 in Academic Trigonometry. Plane and Spherical by T. M. Blakslee.

“Law of Sines. In any plane triangle, the sides are proportional to the sines of the opposite angles.”

“Law of Cosines. The square of any side of a (pl.) triangle is equal to the sum of the squares of the other two sides, minus twice their product by the cosine of the included angle.”

“Law of Tangents. The sum of any two sides of a (pl.) triangle is to their difference as the tangent of one-half the sum of the opposite angles is to the tangent of one-half their difference.”

[Google print search by James A. Landau]

LAW OF SMALL NUMBERS is a translation of the German phrase coined by L. von Bortkiewicz, and used by him as a title of his book Das Gesetz der kleinen Zahlen (1898). (David (2001)). A JSTOR search found the English phrase in a note, probably by Edgeworth, in the Economic Journal (1904, p. 496) on an Italian publication treating “the relation between statistics and the Calculus of Probabilities with special reference to Prof. Bortschevitch’s ‘law of small numbers.’”

LAW OF THE ITERATED LOGARITHM is found in English in Philip Hartman and Aurel Wintner, "On the law of the iterated logarithm," Am. J. Math. 63, (1941), 69-176.

The German name appears in A. Kolmogorov’s Über das Gesetz des iterierten Logarithmus, Mathematische Annalen, 101, (1929), 126-135. Kolmogorov was extending the original result (for coin tossing) due to A. Khintchine "Über einen Satz der Wahrscheinlichkeitsrechnung," Fundamamenta Mathematicae, 6, (1924), 9-20. Khintchine’s work in turn rested on partial results formulated in terms of number theory. [John Aldrich]

The term LEAST ACTION was used by Lagrange (DSB).

The OED says the term principle of least action is from the French principe de la moindre quantité d'action, lit. “principle of the least amount of action,” and attributes this term to Pierre Louis Moreau de Maupertuis in 1748, in Hist. de l'Acad. R. des Sci. et des Belles Lettres de Berlin 1746, 286.

The term is in use in a paper by de Maupertuis in 1744, in French and in English translation. [James A. Landau]

In 1751 the mathematician Samuel König started a priority dispute by claiming the least action principle had been invented by Leibniz in 1707. English language magazine articles in 1752 discussing this dispute used the English term “least action.” See here. [James A. Landau]

LEAST COMMON MULTIPLE. Common denominator appears in English in 1594 in Exercises by Blundevil: "Multiply the Denominators the one into the other, and the Product thereof shall bee a common Denominator to both fractions" (OED).

Common divisor was used in 1674 by Samuel Jeake in Arithmetick, published in 1696: "Commensurable, called also Symmetral, is when the given Numbers have a Common Divisor" (OED).

Least common multiple is found in 1734 in A Treatise of Fractions, in Two Parts by Alexander Wright: “The least Common Multiple to any Numbers is the least Number, which being divided by each of the Numbers proposed, leaves nothing remaining. Thus 12 is a common Multiple to 2, 3, 4, 6, and it is also their least common Multiple.” [Google print search by James A. Landau]

Least common denominator is found in 1751 in A Plain and Familiar METHOD For Attaining the Knowledge and Practice of COMMON ARITHMETIC, 18th ed., by Edmund Wingate: “When 2 or more Fractions having unequal Denominators, are given to be reduced to other equal Fractions having the least common Denominator possible....” [Google print search by James A. Landau]

Lowest common denominator appears in 1777 in Arithmetic, Rational and Practical, 3rd ed., by John Mair: “The lower fractions are reduced, the more simple and easy will any operation be 5 if, therefore, it be required to reduce fractions to the lowest or least common denominator possible, it may be done, as follows ....” [Google print search by James A. Landau]

Least common dividend appears in 1780 in A Treatise of Algebra, in Two Books, Book I, 2nd ed., by W. Emerson. [Google print search by James A. Landau]

Lowest common multiple appears in 1830 in A Treatise on Algebra by George Peacock. [Google print search by James A. Landau]

LEAST SQUARES. See METHOD OF LEAST SQUARES.

LEBESGUE INTEGRAL. In 1899-1901 Henri Lebesgue published five short papers in the Comptes Rendus. These formed the basis of his doctoral dissertation Intégrale, longueur, aire, published in 1902 in the Annali di Matematica. The fifth paper of the series “Sur une généralisation de l’intégral défini,” Comptes rendus 132, (1901) 1025-1028 announced Lebesgue’s generalisation of the Riemann Integral. (From T. Hawkins Lebesgue’s Theory of Integration: Its Origins and Development. 1970)

The term Lebesgue integral soon appeared in English, in a paper by William H. Young, “On an extension of the Heine-Borel Theorem,” Messenger of Mathematics 33 (1903-04), 120-132. The date received by the editors is not given, but Ivor Grattan-Guinness [“Mathematical bibliography for W. H. and G. C. Young,” Historia Mathematica 2 (1975), 43-58] places this paper chronologically between papers with received dates of 29 October 1903 and 6 December 1903.

The theorem in question has, as far as I know, not hitherto been formulated, though it can be deduced without difficulty from a theorem in a recent memoir by M. Lebesgue, which states that the Lebesgue integral, as we may conveniently call it, of a sum of any two functions (as far as our present knowledge of functions goes) is the sum of their Lebesgue integrals. It has only to be shown that the new notion of the Lebesgue integral coincides in the case of semi-continuous functions with the well-known one of upper or lower integral.

(footnote on p. 129)

Behind Young’s reference to the Lebesgue integral is a tale of lost priority. For when Young next refers to the integral he indicates the resemblance between Lebesgue’s work and his own researches. William H. Young, “On upper and lower integration,” Proceedings of the London Mathematical Society (2) (1905), 52-66. [Received by the editors on January 14, 1904. The following footnote appears on the first page of the paper and is dated April 2, 1904.]

This paper was written simultaneously with the preceding memoir [Young’s "Open sets and the theory of content"], at a time when the writer was unacquainted with the work of M. Lebesgue. The result of Theorem 2 is in perfect accord with Lebesgue’s expression for his integral as the common limit of two difference summations (Annali di Matematica, 1902, p. 253); in fact, it is easily shown that, in the case of an (upper) lower semi-continuous function, the Lebesgue integral coincides with the upper (lower) integral. It may be further remarked that, in the general case, the Lebesgue integral may itself be expressed in precisely my form.

In accordance with the alterations made in the preceding memoir (cp. footnote, p. 16), I have made a few verbal alterations in the present paper; I have also elaborated the proof of the final theorem, which, in its original form, was too condensed.

The following is from p. 143 of Ivor Grattan-Guinness, “A mathematical union: William Henry and Grace Chisholm Young,” Annals of Science 29(2) (August 1972), 105-186:

By 1904 Will had, independently of Lebesgue, constructed by different means an equivalent theory of integration. It was his first really important idea in mathematics and the discovery that he had been anticipated would have cracked many a lesser man. But he took it magnanimously; when he heard of Lebesgue’s work he withdrew his major paper and rewrote parts of it to include considerations on what he named for ever as 'the Lebesgue integral'. There were enough technical differences between the two approaches for Young to present his own results in this paper, and sufficient applications of his approach to all branches of analysis to make it significant in its time. In fact, some of the succeeding workers on 'Lebesgue integration' have preferred to follow Young’s rather than Lebesgue’s approach.

[This entry was contributed by Dave L. Renfro.]

LEG for a side of a right triangle other than the hypotenuse is found in English in 1659 in Joseph Moxon, Globes (OED).

Leg is used in the sense of one of the congruent sides of an isosceles triangle in 1702 Ralphson’s Math. Dict.: "Isosceles Triangle is a Triangle that has two equal Legs" (OED).

LEIBNIZ SERIES. See GREGORY’s SERIES.

LEMMA appears in English in the 1570 translation by Sir Henry Billingsley of Euclid’s Elements (OED). [The plural of lemma can be written lemmas or lemmata.]

LEMNISCATE. Jacob Bernoulli named this curve the lemniscus in Acta Eruditorum in 1694. He wrote, "...formam refert jacentis notae octonarii [infinity symbol], seu complicitae in nodum fasciae, sive lemnisci" (Smith vol. 2, page 329).

LEMOINE POINT. See SYMMEDIAN POINT.

LEPTOKURTIC. See KURTOSIS.

LEVERAGE in least squares estimation. The earliest JSTOR appearances are from 1978 but the term was apparently already established for David F. Andrews and Daryl Pregibon write that "observations with large effects" are usually called "leverage points". "Finding the Outliers that Matter," Journal of the Royal Statistical Society. Series B, 40, (1978), 85-93.

L'HOSPITAL’S RULE. In his "De progressionibus transcendentibus" Euler referred to the method as "a known rule" ("per regulam igitur cognitam quaeramus valorem fractionis") [Stacy Langton].

In 1891 in An Elementary Treatise of the Differential and Integral Calculus by George A. Osborne, the method is not named: "The Differential Calculus furnishes the following method applicable to all cases."

In Differential and Integral Calculus (1902) by Virgil Snyder and John Irwin Hutchinson, the procedure is termed "evaluation by differentiation." The same term is used in Elementary Textbook of the Calculus (1912) by the same authors.

de l'Hospital’s theorem on indeterminate forms is found in approximately 1904 in the E. R. Hedrick translation of volume I of A Course in Mathematical Analysis by Edouard Goursat. The translation carries the date 1904, although a footnote references a work dated 1905 [James A. Landau].

The 1906 edition of A History of Mathematics by Florian Cajori, referring to L'Hopital’s 1696 treatise, has: "This contains for the first time the method of finding the limiting value of a fraction whose two terms tend toward zero at the same time."

In Differential and Integral Calculus (1908) by Daniel A. Murray, the procedure is shown but is not named.

James A. Landau has found in J. W. Mellor, Higher Mathematics for Students of Chemistry and Physics, 4th ed. (1912), the sentence, "This is the so-called rule of l'Hopital."

L'Hopital’s rule is dated 1944 in MWCD11.

The rule is named for Guillaume-Francois-Antoine de l'Hospital (1661-1704), although the rule was discovered by Johann Bernoulli. The rule and its proof appear in a 1694 letter from him to l'Hospital.

The family later changed the spelling of the name to l'Hôpital.

LIAR PARADOX. This paradox exists in several forms. One is attributed to the philosopher Epimenides in the sixth century BC: "All Cretans are liars...One of their own poets has said so." Another is attributed to Eubulides of Miletus a leader of the Megarian school from the fourth century BC.  In his Life of Euclides Diogenes Laertius wrote that Eubulides "handed down a great many arguments in dialectic." The Eubulides form is "Is the man a liar who says that he tells lies?" W. & M. Kneale The Development of Logic (1962) pp. 227-8 say that new variants were devised in the Middle Ages and they speculate that the medieval logicians may have rediscovered the paradox from considering Titus 1:12-13: “One of themselves, a prophet of their own, hath said, The Cretans are always liars, evil wild beasts, lazy gluttons. This witness is true. ...” Paul evidently did not see the paradox in this echo of Epimenides.

Paradox of the liar is found in 1940 in An Inquiry Into Meaning And Truth by Bertrand Russell: “The inference from the paradox of the liar is as follows.” [OED]

Liar paradox is found in 1959 in The Foundations of Mathematics: A Study in the Philosophy of Science by Evert Willem Beth: “The natural first reaction to the liar paradox is to ascribe the contradiction to the fact that the statement involved refers to itself.” [OED]

See PARADOX.

LIE GROUP (named for Sophus Lie) appears in L. Autonne, "Sur une application des groupes de M. Lie.," C. R. CXII. 570-573 (1891).

A second 1891 usage is found in “La théorie des goupes continus de transformations due à M. Sophus Lie. ...” [Google print search by James A. Landau]

Lie group appears in English in 1897 in "Sophus Lie’s Transformation Groups: A Series of Elementary, Expository Articles" by Edgar Odell Lovett, The American Mathematical Monthly, Vol. 4, No. 10. [JSTOR search]

LIFE TABLE. John Graunt set down a life table in Chapter XI of Observations Made upon the Bills of Mortality (1662) in the course of estimating the number of "fighting men" in London.

Edmond Halley presented a more solidly based table in "An Estimate of the Degrees of the Mortality of Mankind, Drawn from Curious Tables of the Births and Funerals at the City of Breslaw; With an Attempt to Ascertain the Price of Annuities upon Lives" Philosophical Transactions (1683-1775), Vol. 17. (1693), 596-610.

Life tables appears in 1825 in The Caledonian Mercury: “The life tables from which premiums have hitherto been calculated, are acknowledged to be no longer applicable.” [OED]

Life table appears in 1825 in Tables of Life Contingencies by Griffith Davies: “From the Single Life Table extract the value of ₤1 annuity on each of the proposed lives taken separately, and from the sum deduct that of a similar annuity on their joint existence, found as direct in the last Example.” [Google print search by James A. Landau]

See Hald (1990, chapters 7 and 9) and Life and Work of Statisticians for other presentations of Halley’s article.

See SURVIVAL FUNCTION.

LIKELIHOOD. The term was first used in its modern sense in R. A. Fisher’s "On the "Probable Error" of a Coefficient of Correlation Deduced from a Small Sample", Metron, 1, (1921), 3-32.

Formerly, likelihood was a synonym for probability, as it still is in everyday English. In his paper "On the Mathematical Foundations of Theoretical Statistics" (Phil. Trans. Royal Soc. Ser. A. 222, (1922), p. 326). Fisher made clear for the first time the distinction between the mathematical properties of "likelihoods" and "probabilities" (DSB).

The solution of the problems of calculating from a sample the parameters of the hypothetical population, which we have put forward in the method of maximum likelihood, consists, then, simply of choosing such values of these parameters as have the maximum likelihood. Formally, therefore, it resembles the calculation of the mode of an inverse frequency distribution. This resemblance is quite superficial: if the scale of measurement of the hypothetical quantity be altered, the mode must change its position, and can be brought to have any value, by an appropriate change of scale; but the optimum, as the position of maximum likelihood may be called, is entirely unchanged by any such transformation. Likelihood also differs from probability in that it is not a differential element, and is incapable of being integrated: it is assigned to a particular point of the range of variation, not to a particular element of it.

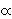Posterior Probability Prior Probability × Likelihood

This entry was contributed by John Aldrich, based on David (2001). See BAYES, MAXIMUM LIKELIHOOD, INVERSE PROBABILITY and POSTERIOR & PRIOR.

LIKELIHOOD PRINCIPLE. This expression burst into print in 1962, appearing in "Likelihood Inference and Time Series" by G. A. Barnard, G. M. Jenkins, C. B. Winsten (Journal of the Royal Statistical Society A, 125, 321-372), "On the Foundations of Statistical Inference" by A. Birnbaum (Journal of the American Statistical Association, 57, 269-306), and L. J. Savage et al, (1962) The Foundations of Statistical Inference. It must have been current for some time because the Savage volume records a conference in 1959; the term appears in Savage’s contribution so the expression may have been his coining.

The principle (without a name) can be traced back to R. A. Fisher’s writings of the 1920s though its clearest earlier manifestation is in Barnard’s 1949 "Statistical Inference" (Journal of the Royal Statistical Society. Series B, 11, 115-149). On these earlier outings the principle attracted little attention. See Likelihood and Probability in R. A. Fisher’s Statistical Methods for Research Workers.

The LIKELIHOOD RATIO figured in the test theory of J. Neyman and E. S. Pearson from the beginning, "On the Use of Certain Test Criteria for Purposes of Statistical Inference, Part I" Biometrika, (1928), 20A, 175-240. They usually referred to it as the likelihood although the phrase "likelihood ratio" appears incidentally in their "Problem of k Samples," Bulletin Académie Polonaise des Sciences et Lettres, A, (1931) 460-481. This phrase was more often used by others writing about Neyman and Pearson’s work, e.g. Brandner "A Test of the Significance of the Difference of the Correlation Coefficients in Normal Bivariate Samples," Biometrika, 25, (1933), 102-109.

The standing of "likelihood ratio" was confirmed by S. S. Wilks’s "The Large-Sample Distribution of the Likelihood Ratio for Testing Composite Hypotheses," Annals of Mathematical Statistics, 9, (1938), 60-620 [John Aldrich, based on David (2001)].

See the entry WALD TEST.

The term LIMAÇON was coined in 1650 by Gilles Persone de Roberval (1602-1675) [Encyclopaedia Britannica, article: "Geometry"].

Limaçon is found in English in 1852 in A Treatise on Higher Plane Curves by G. Salmon: “The origin is a double point, and the curve is of the fourth class, and is the ‘limaçon de Pascal.’” [OED]

The curve is sometimes called Pascal’s limaçon, for Étienne Pascal (1588?-1651), the first person to study it. Boyer (page 395) writes that "on the suggestion of Roberval" the curve is named for Pascal.

LIMIT. Gregory of St. Vincent (1584-1667) used terminus to mean the limit of a progression, according to Carl B. Boyer in The History of the Calculus and its Conceptual Development.

Isaac Newton wrote justifying limits in the Scholium to Section I of Book I of the Principia (Philosophiae Naturalis Principia Mathematica or The Mathematical Principles of Natural Philosophy) (first edition 1687)

Perhaps it may be objected, that there is no ultimate proportion, of evanescent qualities; because the proportion, before the quantities have vanished, is not the ultimate, and when they are vanished, is none. But by the same argument, it may be alledged, that a body arriving at a certain place, and there stopping, has no ultimate velocity: because the velocity, before the body comes to the place, is not its ultimate, velocity; when it has arrived, is none. But the answer is easy; for by the ultimate velocity is meant that with which the body is moved, neither before it arrives at its last place and the motion ceases, nor after, but at the very instant it arrives; that is, that velocity with which the body arrives at its last place, and with which the motion ceases. And in like manner, by the ultimate ratio of evanescent quantities is to be understood the ratio of the quantities not before they vanish, nor afterwards, but with which they vanish. In like manner the first ratio of quantities is that with which they begin to be. And the first or last sum is that with which they begin and cease to be (or to be augmented or diminished). There is a limit which the velocity at the end of the motion may attain, but not exceed. This is the ultimate velocity. And there is the like limit in all quantities and proportions that begin and cease to be. And since such limits are certain and definite, to determine the same is a problem strictly geometrical. But whatever is geometrical we may be allowed to use in determining and demonstrating any other thing that is likewise geometrical. (Translated by Andrew Motte 1729)

Katz (p. 471) comments, "A translation of Newton’s words into an algebraic statement would give a definition of limit close to, but not identical with, the modern one."

In 1821 Augustin-Louis Cauchy defined limit as follows: "If the successive values attributed to the same variables approach indefinitely a fixed value, such that they finally differ from it by as little as one wishes, this latter is called the limit of all the others." Cours d'analyse (Oeuvres II.3), p. 19. (Translation from Katz page 641) Cauchy introduced the modern ε, δ way of arguing.

This entry was contributed by John Aldrich. See also Limit and Delta and epsilon on the Earliest Use of Symbols of Calculus page.

LIMIT POINT is found in 1850 in A Treatise on Conic Sections by George Salmon: “Angle ... Subtended at limit points of system of circles.” [OED]

Cantor used Häufungspunkt (accumulation point) in an 1872 paper “Über die Ausdehnung eines Satzes der Theorie der trigonometrischen Reihen,” which appeared in Mathematische Annalen 5, pp. 123-132. [Roger Cooke]

Point of accumulation appears in English in 1921 in The Theory of Functions of a Real Variable and the Theory of Fourier Series, v. I, by Ernest William Hobson: “A limiting point of G, defined as above, is also called a point of accumulation. Another definition of a limiting point is that it is a point P such that G contains a sequence of points {Pn} for which the distance PPn is less than an arbitrarily chosen ... .” [Google print search by James A. Landau]

LINDLEY’S PARADOX. "An example is produced to show that, if H is a simple hypothesis and x the result of an experiment, the following two phenomena can occur simultaneously: (i) a significance test for H reveals that x is significant at, say, the 5% level; (ii) the posterior probability of H given x, is, for quite small prior probabilities of H, as high as 95%." D. V. Lindley "A Statistical Paradox" Biometrika, 44, (1957), pp. 187-192. Lindley notes that "the paradox is not in essentials new, although few statisticians are aware of it." (p. 190) His earliest reference is to the discussion in Jeffreys’s Theory of Probability on which he comments, "Jeffreys is concerned to emphasise the similarity between his tests and those due to Fisher and the discrepancies are not emphasised." Lindley’s Paradox is the common name although some writers refer to the Jeffreys-Lindley Paradox.

LINE FUNCTION was the term used for functional by Vito Volterra (1860-1940), according to the DSB.

LINE GRAPH is found in 1916 in Combinatorial Analysis by Percy A. MacMahon. [Google print search by James A. Landau]

The term LINE INTEGRAL was used in 1873 by James Clerk Maxwell in a Treatise on Electricity and Magnetism, p. 71 in the phrase "Line-Integral of Electric Force, or Electromotive Force along an Art of a Curve" (OED). Earlier in the book (p. 12) Maxwell explained how "Line-integration [is] appropriate to forces, surface-integration to fluxes." The concept of a line integral is much older: see the entry GREEN’S THEOREM.

The alternate term curve integral has been seen in 1965 textbook, but it may be much older.

The term LINE OF EQUAL POWER was coined by Steiner.

LINEAR ALGEBRA. The DSB seems to imply that the term algebra linearia is used by Rafael Bombelli (1526-1572) in Book IV of his Algebra to refer to the application of geometrical methods to algebra.

Linear algebra is found in English in 1870 in the American Journal of Mathematics (1881)4/107: “An algebra in which every expression is reducible to the form of an algebraic sum of terms, each of which consists of a single letter with a quantitative coefficient, is called a linear algebra.” [OED]

Linear algebra occurs in 1875 in the title, "On the uses and transformations of linear algebra" by Benjamin Peirce, published in American Acad. Proc. 2 [James A. Landau].

Pierce meant what today we would call a "finite dimensional algebra over a field," not the theory of vector spaces and linear transformations. [Fernando Q. Gouvea]

In 1898, Alfred North Whitehead wrote in a footnote in A Treatise on Universal Algebra with applications: “The type of multiplication is then called by Grassman (cf. Audehanungelebre vom 1862, §50) ‘linear.” But this nomenclature clashes with the generally accepted meaning of a ‘linear algebra’ as defined by B. Peirce in his paper on Linear Associative Algebra, American Journal of Mathematics, vol. IV (1881). The theorem of subsection (2) is due to Grassman, cf. loc. cit.” [Google print search by James A. Landau]

LINEAR COMBINATION is found in 1854 in “On a Theory of the conjugate relations of two rational integral functions, comprising an application to the Theory of Sturm’s Functions, and that of the greatest Algebraical Common Measure’ by J. J. Sylvester, in Abstracts of the Papers communicated the the Royal Society of London from 1850 to 1854 inclusive. [Google print search by James A. Landau]

LINEAR DEPENDENCE appears in the title “The Theory of Linear Dependence” by Maxime Bôcher published in 1900 in the Annals of Mathematics [James A. Landau].

LINEAR DIFFERENTIAL EQUATION appears in J. L. Lagrange, "Recherches sur les suites récurrentes don't les termed varient de plusieurs manières différentes, ou sur l'intégration des équations linéaires aux différences finies et partielles; et sur l'usage de ces équations dans la théorie des hasards," Nouv. Mém. Acad. R. Sci. Berlin 6 (1777) [James A. Landau].

LINEAR EQUATION appears in English the 1816 translation of Lacroix’s Differential and Integral Calculus (OED).

LINEAR FUNCTION is found in 1829 in an English translation of Mécanique Céleste by Laplace. [Google print search by James A. Landau]

LINEAR INDEPENDENCE is found in 1846 in “Researches respecting Quaternions. First Series,” by Sir William Rowan Hamilton in Transactions of the Royal Irish Academy. [Google print search by James A. Landau].

LINEAR OPERATOR. Linear operation appears in 1837 in Robert Murphy, "First Memoir on the Theory of Analytic Operations," Philosophical Transactions of the Royal Society of London, 127, 179-210. Murphy used "linear operation" in the sense of the modern term "linear operator" [Robert Emmett Bradley].

LINEAR PRODUCT. This term was used by Hermann Grassman in his Ausdehnungslehre (1844).

LINEAR PROGRAMMING. See PROGRAMMING.

LINEAR TRANSFORMATION appears in 1843 in the title “Exposition of a general theory of linear transformations, Part II” by George Boole in Camb. Math. Jour. t. III. 1843, pp. 1-20. [James A. Landau]

LINEARLY DEPENDENT was used in 1893 in "A Doubly Infinite System of Simple Groups" by Eliakim Hastings Moore. The paper was read in 1893 and published in 1896 [James A. Landau].

LINEARLY INDEPENDENT is found in 1841 in “On a linear Method of Eliminating between double, treble, and other Systems of Algebraic Equations,” by J. J. Sylvester in The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science Vol. XVIII. [Google print search by James A. Landau]

LINK FUNCTION. One of the components of a GENERALIZED LINEAR MODEL is "the linking function, θ = f(Y) connecting the parameter of the distribution of z [the dependent variable] with the Y’s of the linear model." Nelder & Wedderburn Journal of the Royal Statistical Society, A, 135, (1972), p. 372. The term link function was introduced in J. A. Nelder’s "Log Linear Models for Contingency Tables: A Generalization of Classical Least Squares," Applied Statistics, 23, (1974), pp. 323-329. (Based on David (1998))

The term LITUUS (Latin for the curved wand used by the Roman pagan priests known as augurs) was chosen by Roger Cotes (1682-1716) for the locus of a point moving such that the area of a circular sector remains constant, and it appears in his Harmonia Mensurarum, published posthumously in Cambridge, 1722 [Julio González Cabillón].

The term LOCAL PROBABILITY is due to Morgan W. Crofton (1826-1915) (Cajori 1919, page 379).

The term is found in 1865 in James Joseph Sylvester, “On a Special Class of Questions on the Theory of Probabilities,” Birmingham British Association Report 35: “After referring to the nature of geometrical or local probability in general, the author of the paper drew attention to a particular class of questions partaking of that character in which the condition whose probability is to be ascertained is one of pure form. The chance of three points within a circle or sphere being apices of an acute or obtuse-angled triangle, or of the quadrilateral formed by joining four convex quadrilateral, will serve as types of the class of questions in view.”

The term appears in “Note on Local Probability” by Crofton in Mathematical Questions, With Their Solutions, Vol. 7, from January to July 1867: “When, therefore, in questions on Local Probability, we speak of a point or line taken at random, i.e. according to no law, there is no obscurity in the idea; but it cannot be made a matter of arithmetical calculation till we have a definite conception of the nature of the assemblage of points or lines one (or more) of which we take.” [Herb Acree]

LOCATION and SCALE. The location and scaling of frequency curves is discussed in §9 of R. A. Fisher’s "On the Mathematical Foundations of Theoretical Statistics" (Phil. Trans. R. Soc. 1922, p. 338). In §9 of Two New Properties of Mathematical Likelihood (Proc.R. Soc., A, 1934 p. 303) Fisher changed his terminology to the estimation of location and scaling. The terms location parameter and scale parameter were used by E. J. G. Pitman in "Tests of Hypotheses Concerning Location and Scale Parameters," Biometrika, 31, (1939), 200-215.

David (2001)

LOCUS is a Latin translation of the Greek word topos. Both words mean "place."

According to Pappus, Aristaeus (c. 370 to c. 300 BC) wrote a work called On Solid Loci (Topwn sterewn).

Pappus also mentions Euclid in connection with locus problems.

Apollonius mentioned the "locus for three and four lines" ("...ton epi treis kai tessaras grammas topon...") in the extant letter opening Book I of the Conica. Apollonius said in the first book that the third book contains propositions (III.54-56) relevant to the 3 and 4 line locus problem (and, since these propositions are new, Apollonius claimed Euclid could not have solved the problem completely--a claim that caused Pappus to call Apollonius a braggard (alazonikos). In Book III itself there is no mention of the locus problem [Michael N. Fried].

Locus appears in the title of a 1636 paper by Fermat, "Ad Locos Planos et Solidos Isagoge" ("Introduction to Plane and Solid Loci").

In English, locus is found in 1727-41 in Chambers Cyclopedia: "A locus is a line, any point of which may equally solve an indeterminate problem. ... All loci of the second degree are conic sections" (OED).

In English, locus is also found in 1741 in Scots Magazine. [Google print search, James A. Landau}

Locus geometricus is an entry in the 1771 Encyclopaedia Britannica.

LOGARITHM. Before he coined the term logarithmus Napier called these numbers numeri artificiales, and the arguments of his logarithmic function were numeri naturales [Heinz Lueneburg].

Logarithmus was coined (in Latin) by John Napier (1550-1617) and appears in 1614 in his Mirifici Logarithmorum Canonis descriptio.

According to the OED, "Napier does not explain his view of the literal meaning of logarithmus. It is commonly taken to mean 'ratio-number', and as thus interpreted it is not inappropriate, though its fitness is not obvious without explanation. Perhaps, however, Napier may have used logos merely in the sense of 'reckoning', 'calculation.'"

According to Briggs in Arithmetica logarithmica (1624), Napier used the term because logarithms exhibit numbers which preserve always the same ratio to one another.

According to Hacker (1970):

It undoubtedly was Napier’s observation that logarithms of proportionals are "equidifferent" that led him to coin the name "logarithm," which occurs throughout the Descriptio but only in the title of the Constructio, which clearly was drafted first although published later. The many-meaning Greek word logos is therefore used in the sense of ratio. But there is an amusing play on words to which we might call attention since it does not seem to have been noticed. It is interesting that the Greeks also employed logos to distinguish reckoning, or that is to say mere calculation, from arithmos, which was generally reserved by them to indicate the use of number in the higher context of what today we call the theory of numbers. Napier’s "logarithms" have indeed served both purposes.

Logarithm appears in English in 1616 in E. Wright’s English translation of the Descriptio: "This new course of Logarithmes doth cleane take away all the difficultye that heretofore hath beene in mathematicall calculations. [...] The Logarithmes of proportionall numbers are equally differing."

In the Constructio, which was drafted before the Descriptio, the term "artificial number" is used, rather than "logarithm." Napier adopted the term logarithmus before his discovery was announced.

Jobst Bürgi called the logarithm Die Rothe Zahl since the logarithms were printed in red and the antilogarithms in black in his Progress Tabulen, published in 1620 but conceived some years earlier (Smith vol. 2, page 523).

[Older English-language dictionaries pronounce logarithm with an unvoiced th, as in thick and arithmetic.]

See also BRIGGSIAN LOGARITHM, COMMON LOGARITHM, NAPIERIAN LOGARITHM, NATURAL LOGARITHM.

LOGARITHMIC CURVE. Huygens proposed the terms hemihyperbola and linea logarithmica sive Neperiana.

Christiaan Huygens used logarithmica when he wrote in Latin and logarithmique when he wrote in French.

Johann Bernoulli used a phrase which is translated "logarithmic curve" in 1691/92 in Opera omnia (Struik, page 328).

Logarithmic curve is found in English in 1715 in The Elements of Astronomy, Physical and Geometrical by David Gregory and Edmond Halley: "But this is the Property of the Logarithmic Curve very well known to Geometricians; therefore the Curve ACX is a Logarithmic Curve, whose Asymptote is the Right line BZ." [Google print search]

LOGARITHMIC FUNCTION. Lacroix used fonctions logarithmiques in Traité élémentaire de calcul différentiel et de calcul intégral (1797-1800).

Logarithmic function is found in English in 1809 in An Essay on the Theory of the Various Orders of Logarithmic Transcendents by William Spence. [Google print search, James A. Landau]

The term LOGARITHMIC POTENTIAL was coined by Carl Gottfried Neumann (1832-1925) (DSB).

In 1877 the term “logarithmische potential” is found several times in Untersuchungen über das Logarithmische und Newton’sche Potential, and this could be where Neumann introduced the term. [Google print search, James A. Landau]

An early English language usage of logarithmic potential is in 1897 by Arthur Gordon Webster in The Theory of Electricity and Magnetism, Being Lectures on Mathematical Physics. [Google print search, James A. Landau]

The term LOGARITHMIC SPIRAL was introduced by Pierre Varignon (1654-1722) in a paper he presented to the Paris Academy in 1704 and published in 1722 (Cajori 1919, page 156).

Logarithmic spiral is found in English in 1736 in The Doctrine of Fluxions, Founded on Sir ISAAC NEWTON’s Method by James Hodgson. [Google print search, James A. Landau]

Another term for this curve is equiangular spiral.

Jakob Bernoulli called the curve spira mirabilis (marvelous spiral).

LOGIC. The term logikê (knowledge of the functions of logos or reason) was used by the Stoics but it covered many philosophical topics that are not part of the modern subject. According to W. & M. Kneale The Development of Logic (1962) pp. 7 & 23, the word "logic" first appeared in its modern sense in the commentaries of Alexander of Aphrodisias who wrote in the third century AD. Until the late 19^th century the scope of the study was determined by the contents of Aristotle’s (384-322 BC) writings on reasoning. These were assembled by his pupils after his death and became collectively known as the Organon or instrument of science. See Robin Smith’s Aristotle’s Logic.

In the Middle Ages logic was one of the three sciences composing the ‘trivium’, the former of the two divisions of the seven ‘liberal arts’. The other constituents were rhetoric and grammar. The higher division, the ‘quadrivium’ consisted of arithmetic, geometry, astronomy and music. For the English word logic the OED’s earliest quotation is from 1362, the second from the Prologue to Chaucer’s Canterbury Tales: "A Clerk ther was of Oxenford also, That unto logik hadde longe ygo." (c.1386.) See QUADRIVIUM.

Although the "Bibliography of Symbolic Logic" published in the first volume of the Journal of Symbolic Logic (December 1936, pp. 121-216) starts in 1666 with Leibniz, the modern era in logic begins in the 19^th century with the work of Augustus de Morgan (1806-1871) and George Boole (1815-1864). By the end of the century many new terms had been coined, including names for the subject, for the author’s particular take on it and for its various sub-divisions. Some of the names are still in use, although their meaning has often shifted. Some authors kept the new terms distinct, others would use them indifferently, e.g. Bertrand Russell treated "symbolic logic" and "mathematical logic" as interchangeable in his "Mathematical Logic as Based on the Theory of Types," American Journal of Mathematics, 30, (1908), 222-262.

Formal logic and symbolic logic were used as book-titles by De Morgan (1847) and J. Venn (1881) respectively. G. Peano used mathematical logic as the name of his new subject. Its concerns were not those of traditional logic, as he explained to Felix Klein in 1894:  "the aim of Mathematical logic is to analyse the ideas and reasoning which feature especially in the mathematical sciences." (quoted on p. 243 of Grattan-Guinness (2000). E. Schröder used the phrase algebra of logic in the title of his main work, Vorlesungen über die Algebra der Logik (volume 1, 1890).  Logistic (French logistique) was used by Couturat and other speakers at the International Congress of Philosophy in 1904 and was popular for a few decades. The terms deductive logic and inductive logic originated in the 19^th century: W. S. Jevons called one of his books Studies in Deductive Logic (1880) and Venn one of his, The Principles of Empirical or Inductive Logic (1889). Informal logic is a new term, having been in use only since the 1970s; see Leo Groarke’s Informal logic.

This entry was contributed by John Aldrich. See MATHEMATICAL LOGIC. A complete list of the set theory and logic terms on this web site is here. For the symbols of logic see Earliest Use of Symbols.

LOGICISM is the doctrine that mathematics is in some significant sense reducible to logic. It is associated with the Principia Mathematica (1910-1913) of A. N. Whitehead and Bertrand Russell. According to Grattan-Guinness (2000, pp. 479 & 501), the word Logizismus was introduced by A. A. H. Fraenkel Einleitung in der Mengenlehre (1928) and R. Carnap Abriss der Logistik (1929). A JSTOR search found the English word in H. Reichenbach "Logical Empiricism in Germany and the Present State of its Problems," Journal of Philosophy, 33, (1936), p. 143.

This entry was contributed by John Aldrich. See also FORMALISM and INTUITIONISM.

The term LOGISTIC CURVE is attributed to Edward Wright (ca. 1558-1615) (Thompson 1992, page 145), although Wright used the term to refer to the logarithmic curve.

Pierre Francois Verhulst (1804-1849) introduced the term logistique as applied to the sigmoid curve [Julio González Cabillón]. David (1995) gives the citation P. F. Verhulst (1845), "La Loi d' Accroissement de la Population," Nouveaux Mémoires de l'Académie Royale des Sciences et Belles-Lettres de Bruxelles, 18, 1-59. Presumably the term refers to the "log-like" qualities of the curve.

The term logistic regression appears in D. R. Cox "The Regression Analysis of Binary Sequences," Journal of the Royal Statistical Society. Series B (Methodological), 20, (1958), 215-242.

LOGIT first appeared in Joseph Berkson’s "Application to the Logistic Function to Bio-Assay," Journal of the American Statistical Association, 39, (1944), p. 361: "Instead of the observations q_i we deal with their logits l_i = ln(p_i / q_i). [Note] I use this term for ln p/q following Bliss, who called the analogous function which is linear on x for the normal curve ‘probit’." (OED)

See PROBIT.

LOGNORMAL. Logarithmic-normal was used in 1919 by S. Nydell in "The Mean Errors of the Characteristics in Logarithmic-Normal Distributions," Skandinavisk Aktuarietidskrift, 2, 134-144 (David, 1995).

Lognormal was used by J. H. Gaddun in Nature on Oct. 20, 1945: "It is proposed to call the distribution of x 'lognormal' when the distribution of log x is normal" (OED).

The lognormal distribution was apparently first studied when Donald McAlister answered a question put by Francis Galton: to what "law of error" does the geometric mean bear the relationship that the arithmetic mean bears to the normal distribution? See Galton’s The Geometric Mean, in Vital and Social Statistics Proceedings of the Royal Society of London, 29, (1879), 365-367, which prefaced McAlister’s paper "The Law of the Geometric Mean." They did not give a name to the new distribution. However, according to E. T. Whittaker & G. Robinson Calculus of Observations (1924, p. 218), Seidel had asked and answered the same question in 1863.

See also ARITHMETIC MEAN and GEOMETRIC MEAN.

LONG DIVISION is found in 1744 in The Schoolmaster’s Assistant by Thomas Dilworth: “It very seldom happens that the Divisor consists of more than one Denomination; yet because such Divisors may sometimes offer themselves, I will give a few for the reader’s satisfaction, which musst be wrought after the manner of Long Division, and may serve also as proofs to some of the foregoing examples in Multiplication.” [OED]

LORENZ ATTRACTOR. This object was first described by the meteorologist Edward Norton Lorenz in his paper “Deterministic non-periodic flow,” J. Atmos. Sci., 20 : 2 (1963) pp. 130–141. The term “Lorenz attractor” came into use in the 1970s when his work began to be noticed. See MathWorld and the Encyclopedia of Mathematics.

LORENZ CURVE. This diagram was introduced by Max O. Lorenz in his “Methods of Measuring the Concentration of Wealth,” Publications of the American Statistical Association, 9, (Jun., 1905), pp. 209-219. The term Lorenz curve quickly entered circulation—see e.g. W. M. Persons “The Measurement of Concentration of Wealth,” Quarterly Journal of Economics, 24, (Nov., 1909), p. 172. According to M. J. Bowman “A Graphical Analysis of Personal Income Distribution in the United States,” American Economic Review, 35, (1945), p. 617n, “The same idea was introduced almost simultaneously by Gini, Chatelain and Séailles.” The Séailles reference is to his 1910 book La répartition des fortunes en France.

LOSS and LOSS FUNCTION in statistical decision theory.  In the paper establishing the subject ("Contributions to the Theory of Statistical Estimation and Testing  Hypotheses," Annals of Mathematical Statistics, 10, 299-326) Wald referred to "loss" but used "weight function" for the (modern) loss function. He continued to use weight function, for instance in his book Statistical Decision Functions (1950), while others adopted loss function. Arrow, Blackwell & Girshick’s "Bayes and Minimax Solutions of Sequential Decision Problems" (Econometrica, 17, (1949) 213-244) wrote L rather than W for the  function and called it the loss function. A paper by Hodges & Lehmann ("Some Problems in Minimax Point Estimation," Annals of Mathematical Statistics, 21, (1950), 182-197) used loss function more freely but retained Wald’s W.

This entry was contributed by John Aldrich, based on David (2001) and JSTOR. See DECISION THEORY.

The term LOWER SEMICONTINUITY was used by René-Louis Baire (1874-1932), according to Kramer (p. 575), who implies he coined the term. The term appears in Baire’s thesis, “Sur les fonctions de variables réelles,” Annali di Matematica Pura ed Applicata (3) 3 (1899), 1-123, and in his “Sur la théorie des fonctions discontinues, Comptes rendus, 129, (1899) 1010-1013.

The phrase LOWEST TERMS appears in about 1675 in Cocker’s Arithmetic, written by Edward Cocker (1631-1676): "Reduce a fraction to its lowest terms at the first Work" (OED). (There is some dispute about whether Cocker in fact was the author of the work.)

LOXODROME. Pedro Nunez (Pedro Nonius) (1492-1577) announced his discovery and analysis of the curve in De arte navigandi. He called the curve the rumbus (Catholic Encyclopedia).

The term loxodrome is due to Willebrord Snell van Roijen (1581-1626) and was coined in 1624 (Smith and DSB, article: "Nunez Salaciense).

LUCAS-LEHMER TEST occurs in the title, "The Lucas-Lehmer test for Mersenne numbers," by S. Kravitz in the Fibonacci Quarterly 8, 1-3 (1970). The test is named for Edouard Lucas and Dick Lehmer.

The term Lucas’s test was used in 1919 by Leonard Eugene Dickson in History of the Theory of Numbers Volume I Divisibility and Primality “R. E. Powers [footnote 185] verified that 2⁸⁹ - 1 is a prime by use of Lucas’ test on the series 4, 14, 194, . . . .” [Google print search, James A. Landau]

The term LUCAS PSEUDOPRIME occurs in the title "Lucas Pseudoprimes" by Robert Baillie and Samuel S. Wagstaff Jr. in Math. Comput. 35, 1391-1417 (1980): "If n is composite, but (1) still holds, then we call n a Lucas pseudoprime with parameters P and Q ..." [Paul Pollack].

LUDOLPHIAN NUMBER. The number 3.14159... was often called the Ludolphische Zahl in Germany, for Ludolph van Ceulen.

“Ludolphische Zahl” is found in 1781 in Lehrbuch der Mathematik by Berhnard Friedr. Monnich. [Google print search, James A. Landau]

In English, Ludolphian number is found in 1886 in G. S. Carr, Synopsis Pure & Applied Math (OED).

In English, Ludolph’s number is found in 1894 in History of Mathematics by Florian Cajori (OED).

LUNE. Lunula appears in A Geometricall Practise named Pantometria by Thomas Digges (1571): "Ye last figure called a Lunula" (OED).

Lune appears in English in 1704 in Lexicon technicum, or an universal English dictionary of arts and sciences by John Harris (OED).