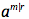 .
Thus the modern n! corresponds to a particular faculté,
viz.
.
Thus the modern n! corresponds to a particular faculté,
viz. 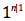 . The German term, die Fakultät, is
a translation of la faculté.
. The German term, die Fakultät, is
a translation of la faculté.Last revision: Feb. 23, 2018
F DISTRIBUTION. The F distribution was tabulated—and the letter introduced—by G. W. Snedecor, Calculation and Interpretation of Analysis of Variance and Covariance (1934) (David, 1995). For this reason it is sometimes called “Snedecor’s F distribution” of the variance-ratio. Snedecor’s goal, however, was not to introduce a new distribution but to improve the presentation of Fisher’s analysis of variance (see the entry VARIANCE). Fisher did not tabulate the variance-ratio, but the statistic z = ½ ln F (see the entry z AND THE z DISTRIBUTION). Fisher was not persuaded that it was better to tabulate the variance-ratio, nor was he happy with the choice of the letter F for the variance-ratio—even if the letter was meant as a compliment to him.
The term F distribution is found in Leo A. Aroian, “A study of R. A. Fisher’s z distribution and the related F distribution,” Annals of Mathematical Statistics, 12, (1941), 429-448.
FACTOR (noun). Fibonacci (1202) used factus ex multiplicatione (Smith vol. 2, page 105).
Factor appears in English in 1673 in Elements of Algebra by John Kersey: "The Quantities given to be multiplied one by the other are called Factors."
FACTOR (verb) appears in English in 1848 in Algebra by J. Ray: "The principal use of factoring, is to shorten the work, and simplify the results of algebraic operations." Factorize (spelled "factorise") is found in 1886 in Algebra by G. Chrystal [OED].
FACTOR and FACTORIAL DESIGN in experimental design. R.A. Fisher introduced the term factor his “The Arrangement of Field Experiments”, Journal of the Ministry of Agriculture of Great Britain, 33, (1926) p. 511. Fisher describes a factorial design in a paper with T. Eden, Studies in Crop Variation. VI. Experiments on the response of the potato to potash and nitrogen, Journal of Agricultural Science, 19, (1929), 201-213 but the term factorial design seems to first appear in Fisher’s book The Design of Experiments (1935): chapter VI is called “The Factorial Design in Experimentation.’ Fisher recalled later (1952, p. 3), “The factorial method of experimentation ... derives its structure, and its name, from the simultaneous inheritance of Mendelian factors.” (David 2001 and Eric Kvaalen.)
FACTOR and FACTOR ANALYSIS in PSYCHOMETRICS. The first factor analysis was in Charles Spearman’s “General intelligence,” objectively determined and measured American Journal of Psychology, 15, (1904), 201-293. However the term factor came later; see e.g. Spearman’s “The theory of two factors,” Psychological Review, 21, (1914), 101-. The term factor analysiscame into circulation in the 1930s. The OED quotes from “Multiple Factor Analysis,” Psychological Review, 38, (1931), 406-427 by Louis L. Thurstone: “It is the purpose of this paper to describe a more generally applicable method of factor analysis which has no restrictions as regards group factors and which does not restrict the number of general factors that are operative in producing the correlations.”
FACTOR GROUP. See QUOTIENT GROUP.
FACTORIAL. The factorial of a natural number n is the product n(n-1)...2.1, usually written n! The German name is die Fakultät. Products of this form appear in early works on combinatorics, such as Jakob Bernoulli’s Ars Conjectandi (1713), and the factorial function and its generalisation, the gamma function, were important topics in European mathematics from the middle of the 17th century; see J. Dutka “The early history of the factorial function”, Archive for History of Exact Sciences, 1991, 43, (3), 225-249. However the modern terms and symbol only appeared at the turn of the 19th century.
Chrétien Kramp
(1760-1826), like other members of the combinatorial school of
Hindenburg,
was interested in notation and terminology; see Cajori
A History of Mathematical Notations
(para. 440-9). In his Analyse des réfractions astronomiques et terrestres (1798)
Kramp gave the existing French word la faculté (= ability) a new meaning.
In Chapter 3, Analyse des facultés numériques, Kramp writes,
“Je désignerai par le
nom de facultés les produits dont
les facteurs constituent une progression arithmétique: tels que a (a+r)
(a+2r)...(a+mr-r).” For
this quantity Kramp introduced the symbol 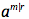 .
Thus the modern n! corresponds to a particular faculté,
viz.
.
Thus the modern n! corresponds to a particular faculté,
viz. 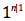 . The German term, die Fakultät, is
a translation of la faculté.
. The German term, die Fakultät, is
a translation of la faculté.
The term factorielle, from which the English word factorial derives, was coined by Kramp’s friend, Louis François Antoine Arbogast (1759-1803). In Arbogast’s Du calcul des derivations (1800, p. 364) the product m(m-r)(m-2r)....(m-nr+r) is called une quantité factorielle or simply une factorielle. Kramp endorsed the term in his Élémens d'arithmétique universelle (Preface, pp. xi-xii, 1808):
...je leur avais donné le nom de facultés. Arbogast lui avait substitué la nomination plus nette et plus française de factorielles; j'ai reconnu l'avantage de cette nouvelle dénomination; et en adoptant son idée, je me suis félicité de pouvoir rendre hommage à la mémoire de mon ami. [...I have called them facultés. Arbogast has substituted the name factorielle, clearer and more French. I have recognised the advantage of this new term, and, in adopting his idea, have welcomed the opportunity to pay tribute to the memory of my friend.]
The exclamation mark notation was introduced in the same work.
At the beginning of the 19th century there were two words for essentially the same thing. One word survives in modern German, the other in modern French and English. In all three languages the modern concept is more specialised than the original: one of the factorials has become the factorial. Some 19th century writers took advantage of the two-word situation: thus in Chrystal’s Algebra (1886-9) faculty is used in Kramp’s original sense and factorial in the modern sense. The situation proved to be temporary and faculty has not survived in mathematical English.
For more information see SYMBOLS IN COMBINATORIAL ANALYSIS on the Symbols in Probability and Statistics page.
[This entry was contributed by John Aldrich.]
The FAST FOURIER TRANSFORM was proposed by J. W. Cooley and J. W. Tukey, "An Algorithm for the Machine Calculation of Complex Fourier Series" Mathematics of Computation, 19, (1965), 297-301. The name Fast Fourier Transform quickly entered circulation. A JSTOR search found it in 1966 in the notice of a paper by C. Bingham and Tukey American Mathematical Monthly, 73, (1966), p. 1038.
H. H. Goldstine A History of Numerical Analysis from the 16th through the 19th Century (1977, p. 249) describes Cooley and Tukey as "rediscovering" work by Gauss.
FEJÉR KERNEL. The Fejér kernel appears for the first time in Fejér, L., “Sur les fonctions bornées et intégrables,” Comptes Rendus Hebdomadaries, Seances de l'Academie de Sciences, Paris 131 (1900), 984-987. [Barry Simon]
The term Fejér kernel appears in 1937 in Differential and Integral Calculus, 2nd. ed. by R. Courant: “The expression sm is called the ‘Fejér kernel’, and is of great importance in the more advanced study of Fourier series.” [James A. Landau]
See also KERNEL.
FERMAT’s LAST THEOREM. Fermat’s General Theorem (referring to this theorem) appears in 1811 in An Elementary Investigation of the Theory of Numbers by Peter Barlow [James A. Landau].
Fermat’s last theorem appears in the title of Gabriel Lamé’s "Memoire sur le dernier theoreme de Fermat," C. R. Acad. Sci. Paris, 9, 1839, pp. 45-46. Lamé explained the reason for the term:
De tous les theoremes sur les nombres, enonces par Fermat, un seul reste incompletement demontre. [Of all the theorems on numbers stated by Fermat, just one remains incompletely demonstrated (proved).]In his Rapport sur un memoire de M. Lamé, Cauchy remarks:
L'Academie nous a charges, M. Liouville et moi, de lui rendre compte d'un Memoire de M. Lamé sur le dernier theoreme de Fermat. [The Academy has charged us, Mr Liouville and myself, to review memoir of Mr. Lamé on the last theorem of Fermat.]This citation is from C. R. Acad. Sci. Paris, 9, 1839, pp. 359-363.
Fermat’s Undemonstrated Theorem appears in 1845 in Phil. Mag. XXVII. 286 [OED].
James Joseph Sylvester concluded an 1847 paper as follows: "I venture to flatter myself that as opening out a new field in connexion with Fermat’s renowned Last Theorem, and as breaking new ground in the solution of equations of the third degree, these results will be generally allowed to constitute an important and substantial accession to our knowledge of the theory of numbers."
An early use of the phrase "Last Theorem of Fermat" in English appears in "Application to the Last Theorem of Fermat" (1860), in "Report on the Theory of Numbers", part II, art. 61, addressed by Henry J. S. Smith.
The OED2 has this 1865 citation from A Dictionary of Science, Literature, and the Arts, by William T. Brande and Cox: "Another theorem, distinguished as Fermat’s last Theorem, has obtained great celebrity on account of the numerous attempts that have been made to demonstrate it."
In May 1816, Carl Friedrich Gauss (1777-1855) wrote a letter to Heinrich Olbers in which he mentioned the theorem. According to an English translation (Singh, p. 105; also an Internet web page), he referred to the theorem as Fermat’s Last Theorem. However, in fact Gauss wrote, "Ich gestehe zwar, dass das Fermatsche Theorem als isolierter Satz fuer mich wenig Interesse hat..." (I confess that the Fermat theorem holds little interest for me as an isolated result...)
Peter Flor writes:
Since your website treats “Fermat’s Little Theorem,” it may be interesting to add that in German, his “Last Theorem” used to be called “Der grosse Satz von Fermat” (Fermat’s Big Theorem) or, for short, “Der grosse Fermat”; alternatively, it was, of course, also referred to as Fermat’s conjecture. Strangely enough — strangely, that is, for German speaking mathematicians — when the novel Fermat’s Last Theorem by Simon Singh was translated into German, the title was translated verbatim as Fermats letzter Satz. I do not know whether the translator was ignorant of its traditional German name or decided for his own reasons to pass it by.
[Julio González Cabillón and William C. Waterhouse contributed to this entry.]
FERMAT’S LITTLE THEOREM is found in 1913 in Zahlentheorie by Kurt Hensel: "Für jede endliche Gruppe besteht nun ein Fundamentalsatz, welcher der kleine Fermatsche Satz genannt zu werden pflegt, weil ein ganz spezieller Teil desselben zuerst von Fermat bewiesen worden ist." [There is a fundamental theorem holding in every finite group, usually called Fermat’s little Theorem because Fermat was the first to have proved a very special part of it.]
This citation was provided by Peter Flor to a math history mailing list.
Little Fermat theorem is found in 1939 in Elementary Number Theory by James Victor Uspensky: “Fermat states a result of which an important theorem, now known as the ‘little Fermat theorem,’ is a consequence. In modern notation this theorem amounts to the statement that ap - 1 = 1 mod p.” [Google print search by James A. Landau]
Fermat’s "little theorem" is found in English in Irving Kaplansky, "Lucas’s Tests for Mersenne Numbers," American Mathematical Monthly, 52 (Apr., 1945) [W. Edwin Clark].
FIBER, FIBER BUNDLE, and FIBER SPACE. According to J. Dieudonné A History of Algebraic and Differential Topology 1900-1960 p. 387, the terms “fiber” (German “Faser”) and “fiber space” (“gefaserter Raum”) probably first appeared in Herbert Seifert “Topologie dreidimensionaler gefaserter, Räume,” Acta Mathematica, 60, (1932), 147-238. However, Dieudonné adds that Seifert’s definitions “are limited to a very special case and his point of view is rather different from the modern concepts.” The modern concepts appear in the 1940s principally in the work of Hassler Whitney. Whitney defines a fibre-bundle in “On the Theory of Sphere-Bundles”, Proceedings of the National Academy of Sciences of the United States of America, 26, No. 2 (Feb. 15, 1940), p. 148. Within a few years the related terms bundle, fibre and fibre space appeared: see N. Steenrod The Topology of Fibre Bundles (1951). In recent years the spelling fiber has become usual, conforming to common US usage. See the MathWorld entry.
FIBONACCI (as a name for Leonardo of Pisa). There is no evidence that the name Fibonacci was ever used by Leonardo or his contemporaries.
In Baldassarre Boncompagni, Della vita e delle opere di Leonardo Pisano matematico del secolo decimoterzo (1852), Baldassarre Boncompagni listed the writers who used the name "Fibonacci":
John Leslie 1820He also listed writers who explaine "Fibinacci = filio Bonacci"
P. D. Pietro Cossali 1797-99
Giovanni Gabriello Grimaldi 1790-1792
Guillaume Libri 1838-1841
Chasles 1837
Nicollet 1811-1818
S. Ersch & I. G. Gruber 1818 and subsequent years
August de Morgan 1847 (he also used Bonacci)
Flaminio dal Borgo 1765Then his arguments for Fibonacci = de filiis Bonacci follow.
Tiraboschi 1822-1828
Ranieri Tempesti 1787
Giovanni Andres 1808-1817
Grimaldi 1790-1792
Libri 1838-1841
According to Boncompagni, Cossali wrote in Origine, trasporto in Italia, primi progressi in essa dell' algebra (2 vols., Parma 1797-1799) the following, on the last page of volume II:
Nel corso dell'Opera ho chiamato il benemerito Leonardo di Pisa, Leonardo Bonacci, laddove da altri fu detto Leonardo Fibonacci, accozzando la prima sillaba Fi di filius al paterno nome Bonacci. Io ho stimato di volger questo a cognome, come assai volte si è fatto. A taluno sarebbe forse piu\ piacciuto (sic) il dire Leonardo di Bonacci.However, according to Menso Folkerts, Cossali gives on page 1, volume 1, Leonardo’s name as "Leonardo Bonacci di Pisa." Later on he only has "Leonardo". In the summary, printed at the beginning of the book, Cossali writes "Leonardo Pisano".
Leonardo Fibonacci appears on pages 2 and 109 in Scritti inediti del P. D. Pietro Cossali. Edited by B. Boncompagni. Roma 1857.
On page 20 of volume two of "Histoire des sciences mathematiques en Italie" (1838) by the historian of mathematics Guillaume Libri (1803-1869) a footnote begins:
Fibonacci est une contraction de filius Bonacci, contraction dont on trouve de nombreux exemples dans la formation des noms des familles toscanes.According to Victor Katz in A History of Mathematics (p. 283), "Leonardo [of Pisa], often known today by the name Fibonacci (son of Bonacci) given to him by Baldassarre Boncompagni, the nineteenth century editor of his works, was born around 1170."
[Most of this entry was taken from a post to the historia matematica mailing list by Heinz Lueneburg.]
FIBONACCI NUMBER is dated 1890-95 in RHUD2.
Fibonacci number is found in 1908 in Types of Floral Mechanism: “In fact 89 as a Fibonacci number would give the most even radial distribution.” [Google print search]
Fibonacci number is found in 1908 in Botanical Gazette: “There is no indication in this species that the Fibonacci numbers tend to predominate.” [Google print search]
The term FIBONACCI SEQUENCE was coined by Edouard Anatole Lucas (1842-1891) (Encyclopaedia Britannica, article: "Leonardo Pisano").
FIBONACCI SERIES. Fibonacci’s series is found in 1891 in the Century Dictionary: Fibonacci’s series, the phyllotactic succession of numbers 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 etc. These numbers are such that the sums of any two successive ones gives the next, a property possessed also by the 2, 1, 2, 4, 7, 11, 18, 29, 47, 76 etc. and by no other series except derivatives of these. The series named from the Italian mathematician Fibonnaci or Leonardo of Pisa (first part of the thirteenth century) who first considered it. Also called Lucas’s series.” [James A. Landau]
FIDUCIAL PROBABILITY and FIDUCIAL DISTRIBUTION first appeared in R. A. Fisher’s 1930 paper “Inverse Probability”, Proceedings of the Cambridge Philosophical Society, 26, 528-535. On p. 533 Fisher writes: “we may know as soon as T is calculated what is the fiducial per cent. value of θ, and that the true value of θ will be less than this value in just 5 per cent. of trials. This then is a definite probability statement about the unknown parameter θ, which is true irrespective of any assumption as to its a priori distribution.” (David (2001)). See the entry BEHRENS-FISHER.
FIELD (neighborhood). In 1893 in A treatise on the theory of functions J. Harkness and F. Morley used the word field in the sense of an interval or neighborhood:
The function f(x) is said to be continuous at the point c ... if a field (c-h to c+h) can be found such that for all points of this field, |f(x)-f(c)| < epsilon.The term field is not defined therein, suggesting the authors believed it was a common usage.
FIELD (modern definition). The term Zahlenkörper (body of numbers) is due to Richard Dedekind (1831-1916) (Kline, page 1146). Dedekind used the term in his lectures of 1858 but the term did not come into general use until the early 1890s. Until then, the expression used was "rationally known quantities," which means either the field of rational numbers or some finite extension of it, depending on the context.
Zahlkörper (number-body) appears in Stetigkeit und Irrationale Zahlen (Continuity & Irrational Numbers):
Dieses System, welche ich mit R bezeichnen will, besitzt vor allen Dingen eine Vollständigkeit und Abgeschlossenheit, welche ich an einem anderen Orte *) als Merkmal eines Zahlkörpers bezeichnet habe, und welche darin besteht, daß die vier Grundoperationen mit je zwei Individuen in R stets ausführbar sind, d. h. daß das Resultat derselben stets wieder ein bestimmtes Individuum in R ist, wenn man den einzigen Fall der Division durch die Zahl Null ausnimmt (This system, which I will denote with R, possesses above all things a completeness and self-containedness, which I, in another place*) , have described as characteristic of a Zahlkörper (number body), and which consist in that the four fundamental operations between any two individuals in R always are possible, that is, that the result of the same (derselben) is always again a definite individual in R, if one excludes the single case of division by the number zero.)Dedekind used Zahlenkörper in Supplement X of his 4th edition of Dirichlet’s Vorlesungenueber Zahlentheorie, section 159. In a footnote, he explained his choice of terminology, writing that, in earlier lectures (1857-8) he used the term 'rationalen Gebietes' and he says that Kronecker (1882) used the term 'Rationalitaetsbereich'.
Dedekind did not allow for finite fields; for him, the smallest field was the field of rational numbers. According to a post in sci.math by Steve Wildstrom, "Dedekind’s 'Koerper' is actually what we would call a division ring rather than a field as it does not require that multiplication be commutative."
Eliakim Hastings Moore (1862-1932) was apparently the first person to use the English word field in its modern sense and the first to allow for a finite field. He coined the expressions "field of order s" and "Galois-field of order s = qn." These expressions appeared in print in December 1893 in the Bulletin of the New York Mathematical Society III. 75. The paper was presented to the Congress of Mathematics at Chicago on Aug. 25, 1893:
Perhaps because of the older mathematical meaning of the English word field, Moore seems to have been very careful in systematically referring to a field of order s and not the shorter term field.3. Galois-field of order s = qn Suppose that we have a system of symbols or marks, µ1, µ2 ... µs, in numbers s, and suppose that these s marks may be combined by the four fundamental operations of algebra ... and that when the marks are so combined the results of these operations are in every case uniquely determined and belong to the system of marks. Such a system of s marks we call a field of order s.
The most familiar instance of such a field, of order s = q = a prime, is the system of q incongruous classes (modulo q) of rational integral numbers a. [...]
It should be remarked further that every field of order s is in fact abstractly considered a Galois-field of order s = qn.
At any event, a decade later Edward V. Huntington wrote:
Closely connected with the theory of groups is the theory of fields, suggested by GALOIS, and due, in concrete form, to DEDEKIND in 1871. The word field is the English equivalent for DEDEKIND’s term Körper;. KRONECKER’s term Rationalitätsbereich, which is often used as a synonym, had originally a somewhat different meaning. The earliest expositions of the theory from the general or abstract point of view were given independently by WEBER and by Moore, in 1893, WEBER’s definition of an abstract field being substantially as follows: [...]The following footnote makes it clear that term field already had the same mathematical meaning at the turn of the century as it does now:The earliest sets of independent postulates for abstract fields were given in 1903 by Professor Dickson and myself; all these sets were the natural extensions of the sets of independent postulates that had already been given for groups.
The most familiar and important example of an infinite field is furnished by the rational numbers, under the operations of ordinary addition and multiplication. In fact, a field may be briefly described as a system in which the rational operations of algebra may all be performed (excluding division by zero). A field may be finite, provided the number of elements (called the order of the field) is a prime or a power of a prime.The quote above is from a paper by Huntington presented to the AMS on December 30, 1904, and received for publication on February 9, 1905.
[Information for this article was contributed by Julio González Cabillón, Heinz Lueneburg, William Tait, Sam Kutler, and Robert Eldon Taylor].
FILTER as a term in control engineering and time series analysis derives from its use in radio engineering, a use the OED traces to around 1920. N. Wiener motivates the problem of filtering as follows: "Very often the quantity which we really wish to observe is observable only after it has been in some way corrupted or altered, by mixture, additively or not, with other time series." Extrapolation, Interpolation and Smoothing of Stationary Time Series (1949, p. 9)
FILTER in topology. J. L. Kelley General Topology (1955, p. 83) writes, "the definition of filter is due to H. Cartan; his treatment of convergence is given in full" in N. Bourbaki Topologie générale, 1940-49.
FINITARY, FINITIST and FINITISM derive from the German word finit used by David Hilbert in his writings on the foundations of mathematics: finitary methods involve only intuitively conceivable objects and performable processes. In his essay on the infinite, “Über das Unendliche,” Mathematische Annalen, 95, (1926), 161-190, Hilbert wrote about “der finite Standpunkt” (point of view). He further explained his ideas in Hilbert and Bernays Grundlagen der Mathematik (1934) I. pp. 32-4.
The word finit came from grammar—as in a finite verb—and was not the word for finite in a mathematical sense: that was endlich. Commentators in English responded with the terms finitist, finitism and finitary. The OED quotes from F. P. Ramsey’s Foundations of Mathematics (1931) p. 243: “Provable ... means provable in any number of steps, and on finitist principles the number must in some way be limited, e.g. to the humanly possible.” Finitism appears in the title of A. Ambrose’s “Finitism in Mathematics (I),” Mind, 44, (1935), 186-203. Both words had been used earlier in other contexts but finitary was coined specially. It appears in quotes in A. J. Kempner’s “Remarks on ‘Unsolvable’ Problems,” American Mathematical Monthly, 43, (1936), 467-473 but contributors to the Journal of Symbolic Logic removed the quotes and it became the standard term.
FINITE appears in English in 1570 in Sir Henry Billingsley’s translation of Euclid’s Elements [OED].
FINITE CHARACTER. This set-theoretic term - usually applied to "properties" ("collections") of sets - was introduced by John Tukey (1915- ) in Convergence and uniformity in topology, Annals of Math. Studies, No 2, Princeton University Press, 1940, p. 7. Tukey’s lemma (a useful equivalent of the axiom of choice) states that every non-empty collection of finite character has a maximal set with respect to inclusion. This result is also known as the "Teichmüller-Tukey lemma" because Oswald Teichmüller (1913-1943) had arrived at it independently in Braucht der Algebriker das Answahlaxiom?, Deutsche Mathematik, vol. 4 (1939), pp. 567-577 [Carlos César de Araújo].
FINITE DIFFERENCE. See CALCULUS OF FINITE DIFFERENCES.
FINITE MATHEMATICS. The April 1918 American Mathematical Monthly states on page 187 that Henry M. Sheffer, instructor in philosophy, gave a program titled “Finite Mathematics” to the Harvard University Mathematics Club on Feb. 20, 1918. No further information is given. [Google print search by James A. Landau]
An Associated Press dispatch appearing in newspapers of Dec. 24, 1955, has: “A course at Dartmouth College in finite mathematics, offered for the first time last year, will be made more difficult this year.”
The book that came out of the course was John G. Kemeny; J. Laurie Snell and Gerald L. Thompson’s Introduction to Finite Mathematics (1957). The book popularised the phrase and the bundle of topics it signified. The preface explains that the book was designed for a different kind of freshman mathematics course treating problems which did not involve "infinite sets, limiting processes, continuity, etc.," and which included "applications to the biological and social sciences."
See DISCRETE MATHEMATICS.
FINITE POPULATION CORRECTION. A JSTOR search found this term in use in Morris H. Hansen and William N. Hurwitz “Relative Efficiencies of Various Sampling Units in Population Inquiries,” Journal of the American Statistical Association, 37, (1942), 89-94. The idea is much older.
FIRST DERIVATIVE, SECOND DERIVATIVE, etc. Christian Kramp (1760-1826) used the terms premiére dérivée and seconde dérivée (first derivative and second derivative) (Cajori vol. 2, page 67). The terms appear in his Élémens d’arithmétique universelle (1808).
The DSB implies Joseph Louis Lagrange (1736-1813) introduced these terms in his Théorie des fonctions. It would seem, however, that he uses phrases that would be translated “first derived function” and “third derived function,” etc. [James A. Landau]
First derivative is found in English in 1838 in Mathematical Treatises, Containing I. The Theory of Analytical Functions II Spherical Trigonometry, with Practical and Nautical Astronomy.
page 9: In which series, fx is the primitive, and f'x, f''x, f'''x, &c. its derivative functions; f'x being the first derivative or prime function, f''x the second derivative, &c.; ....page 13: Thus, to find the first derivative function of any given power of a variable quantity, we have this
RULE. Multiply the given index into the power of the variable, whose index is less by an unit that the given one, and the product is the prime function required.
Page 49: But if the second derivative vanish, there can be no maximum or minimum, unless the third derivative also vanish; in which case we are to proceed with third and fourth derivative as with the first and second: And so on.
[Google print search by James Landau]
FISHER INFORMATION. See INFORMATION, AMOUNT OF.
FISHER’s EXACT TEST. R. A. Fisher gave this test for independence in contingency tables in the 5th edition (1934) of Statistical Methods for Research Workers. F. Yates and J. O. Irwin also published the test. In his "Contingency Tables Involving Small Numbers and the χ2 Test," Supplement to Journal of the Royal Statistical Society, 1, (1934), 217-235) Yates wrote that Fisher had suggested to him "that the probability of any observed set of values in a 2 × 2 contingency table with given marginal totals can be exactly determined." (p. 217) Later he said he suspected that Fisher had already worked it out. Irwin’s paper was "Tests of Significance for Differences between Percentages Based on Small Numbers," Metron, 12, 83-94. Although he had also worked at Fisher’s Rothamsted, his work seemed to be independent of Fisher (and Yates).
Fisher’s discussion was much the most visible and the test usually goes by his name. Thus E. B. Wilson referred to "Fisher’s exact method" ("The Controlled Experiment and the Four-Fold Table," Science, New Series, 93, (1941), 557-560) and G. A. Barnard to "Fisher’s exact test" (Significance Tests for 2×2 Tables," Biometrika, 34, (1947) 123-138.) The Fisher-Yates label is next in popularity: see e.g. D. J. Finney "The Fisher-Yates Test of Significance in 2 × 2 Contingency Tables," Biometrika, 35 (1948), 145-156. References to Irwin alone are rare but Fisher-Irwin is quite common and Fisher-Irwin-Yates just about exists: see for example P. Armitage’s review of D. J. Finney et al. Tables for Testing Significance in a 2X2 Contingency Table, in Journal of the Royal Statistical Society. Series A (General), 127, (1964), 303 [John Aldrich].
See YATES’s CORRECTION.
FISHER’S z TRANSFORMATION OF THE CORRELATION COEFFICIENT. The standard (product moment) formula for estimating the correlation coefficient of a bivariate normal distribution was given by Karl Pearson in his 1896 paper, "Mathematical Contributions to the Theory of Evolution. III. Regression, Heredity and Panmixia," Philosophical Transactions of the Royal Society of London. A, 187, p. 265. Pearson also described how to make inferences using a large sample normal approximation. Student realised that this approximation could be very bad: see his "Probable Error of a Correlation Coefficient," (1908), Biometrika, 6, 302-310. In 1915 R. A. Fisher confirmed Student’s observation and went futher by obtaining the exact distribution of the correlation coefficient Frequency Distribution of the Values of the Correlation Coefficient in Samples from an Indefinitely Large Population.) This paper was a great theoretical achievement but it did not help the practical worker. In 1921 Fisher proposed a transformation of the correlation coefficient which would be approximately normal (On the "Probable Error" of a Coefficient of Correlation Deduced from a Small Sample.) In 1925 he put this z transformation into chapter VI (section 35) of his Statistical Methods for Research Workers. This very influential book made the transformation easily accessible and it came into general use.
A JSTOR search found the phrase "R. A. Fisher’s z-transformation" in Chesire, Oldis & E. S. Pearson "Further Experiments on the Sampling Distribution of the Correlation Coefficient," Journal of the American Statistical Association, 27, (1932), p. 127 [John Aldrich].
See CORRELATION..
FIXED POINT (arithmetic) seems to occur in 1951 in an IBM publication Computation Seminar: “In the case of the calculation of chemical equilibria, for example, a single routine may be used for almost the entire range of possible parameters if the calculations are performed in floating point notation. With fixed point computations, however, approximately thirty-five different routines may be required for the... .” [Google print search by James A. Landau. It is a snippet view but seems to be valid.]
FLOATING POINT is found in 1946 in Preliminary Discussion of the Logical Design of an Electronic Computer Instrument by Arthur Walter Burks, Herman Heine Goldstine, and John Von Neumann: "The first advantage of the floating point is, we feel, somewhat illusory. In order to have such a floating point one must waste memory capacity which could otherwise be used for carrying more digits per word." [Google print search]
The terms FLUXION and FLUENT are associated with Isaac Newton, but Richard Suiseth (also known as Calculator; fl. 1350) used the words fluxus and fluens in his Liber calculationum, according to Carl B. Boyer in The History of the Calculus and its Conceptual Development.
Newton used fluent in 1665 to represent any relationship between variables (Kline, page 340). The word fluxion appears once, perhaps by an oversight, in the Principia (Burton, page 377).
Newton composed the treatise Method of Fluxions in Latin in 1671. [It was first published in 1736, translated into English.] Newton wrote (in translation): "Now those quantities which I consider as gradually and indefinitely increasing, I shall hereafter call fluents, or flowing quantities, and shall represent them by the final letters of the alphabet, v, x, y, and z; ... and the velocities by which every fluent is increased by its generating motion (which I may call fluxions, or simply velocities, or celerities), I shall represent by the same letters pointed...."
FOCUS (of a conic section). Carl Boyer writes in A History of Mathematics, "As the curves are now introduced in textbooks, the foci play a prominent role, yet Apollonius had no names for these points, and he referred to them only indirectly."
The term focus (of an ellipse) was introduced by Johannes Kepler (1571-1630) in a treatment of the conic sections in his Ad Vitellionem paralipomena, quibus Astronomiae pars optica traditur (1604).
Umbilic point is an entry in 1700 in Joseph Moxon’s dictionary of mathematics: "Umbilique Points, or the 2 Focus or Centre-Points in an Elipsis."
FOIL is found in 1929 in Algebra For Today, Book I, by William Betz: “first terms, outer terms, inner terms, last terms. (The rule stated above may also be remembered by the word FOIL, suggested by the first letters of the words first, outer, inner, last.)” The word may also appear in the 1928 edition of this book. [James A. Landau]
The term FOKKER-PLANCK EQUATION recalls the work of two physicists on BROWNIAN MOTION: A. D. Fokker "Die mittlere Energie rotierender elektrischer Dipole im Strahlungsfeld" Annalen der Physik 43, (1914) 810-820 and M. Planck Ueber einen Satz der statistichen Dynamik und eine Erweiterung in der Quantumtheorie, Sitzungberichte der Preussischen Akadademie der Wissenschaften (1917) p. 324-341.
The same equation was obtained by A. N. Kolmogorov in his fundamental paper on MARKOV PROCESSES: "Über die analytischen Methoden in der Wahrscheinlichkeitsrechnung," Math. Ann. 104, (1931), 415-458. Kolmogorov (p. 450) referred to it as the second fundamental differential equation. It has since become known as the Kolmogorov forward equation. The first equation (p. 447) is now called the backward equation. According to E. B. Dynkin, Kolmogorov was not familiar with the papers of Fokker and Planck in 1931 but from 1934 he referred to the Fokker-Planck equation. Dynkin adds that the backward equation had not previously appeared. ("Kolmogorov and the Theory of Markov Processes," Annals of Probability, 17, (1989), p. 823.) See the Encyclopedia of Mathematics article Kolmogorov equation.
Independently the geneticist R. A. Fisher studied the same equation. Fréchet wrote to him in 1936:
In my recent travelling in Russia, Prof. Kolmogoroff--who is one of the half dozen best "probabilists" in the world--observed to me that you have recently come to a differ. equation without probably knowing that it has been met before in a physical problem by Fokker and Planck. It may interest you to hear that it is called Fokker-Planck’s equation ... (p. 261) of Fisher Correspondence.
Fisher’s paper was The Distribution of Gene Ratios for Rare Mutations (1930). D. G. Kendall recalls, “Will Feller used to say that if Kolmogorov had not written his 1931 paper, the whole of stochastic diffusion theory would eventually have been pieced together starting with the ideas in Fisher’s book [The Genetical Theory of Natural Selection (1930)].” (Bulletin of the London Mathematical Society, 22, (1990) p. 34.)
[This entry was contributed by John Aldrich.]
FOLIUM OF DESCARTES. According to Eves (page 302), Barrow called this curve la galande.
Roberval, through an error, was led to believe the curve had the form of a jasmine flower, and he gave it the name fleur de jasmin, which was afterwards changed (Smith vol. 2, page 328).
Folium de Descartes is found in 1845 in Comptes rendus hebdomadaires des séances de l’Académie des sciences. [Google print search by James A. Landau]Folium of Descartes was used in English in 1848 in Differential Calculus (1852) by Bonamy Price [OED].
The curve is also known as the noeud de ruban.
FOLK THEOREM. This term became very popular in the English literature by the middle of the twentieth century. It is just what the name implies: a result (usually not very deep) which belongs to the "folklore." As far as I know, the first to offer an explicit definition was E. J. McShane in his Retiring Presidential Address ("Maintaining Communication," Amer. Math. Monthly, 1957, 309-317):
One hears of "folk theorems", established (presumably) by some expert, communicated verbally or more likely mentioned in an off-hand way during some conversation with another expert or two, and thereafter unpublishable forevermore because no one would want to publish a "known theorem."[This entry was contributed by Carlos César de Araújo.]
FORMALISM in the philosophy of mathematics. The term was coined, not by a "formalist," but by the main critic of "formalism," L. E. J. Brouwer. In his 1912 inaugural lecture at the University of Amsterdam, which appeared in English as "Intuitionism and Formalism," Bull. Amer. Math. Soc. 20, (1913), 81-96, Brouwer wrote
On what grounds the conviction of the unassailable exactness of mathematical laws is based has for centuries been an object of philosophical research, and two points of view may here be distinguished, intuitionism (largely French) and formalism (largely German). ... The question where mathematical exactness does exist, is answered differently by the two sides; the intuitionist says: in the human intellect, the formalist says: on paper. (pp. 82-3, OED)
Hilbert is not mentioned in this paper but he later became the main target of Brouwer’s criticisms of formalism. See also INTUITIONISM and LOGICISM.
FORMULA appears in the phrase "an algebraic formula" in 1796 in Elements of Mineralogy by Richard Kirwan [OED].
FOUR-COLOR PROBLEM. The problem itself dates to 1852, when Francis Guthrie, while trying to color the map of counties of England, noticed that four colors sufficed.
The first printed reference is due to Cayley in 1878, "On the colourings of maps.," Proc. Royal Geog. Soc. 1 (1879), 259-261.
Problem of the four colors appears in A. B. Kempe, "On the geographical problem of the four colors," Amer. J. Math., 2 (1879), 193-200.
"Map-Colour Theorem" is the title of a paper by Percy John Heawood (1861-1955) which appeared in the Quarterly Journal of Pure and Applied Mathematics in 1890.
Four colour theorem is found in 1908 in Bulletin of the American Mathematical Society, Vol XIV October 1907 to July 1908. [Google print search by James A. Landau]
Four color problem is found in 1912 in Bulletin of the American Mathematical Society. [Google print search by James A. Landau]
Four-color map theorem is found in R. P. Baker, "The four-color map theorem," American M. S. Bull. (1916).
Four color conjecture is found in April 1960 in the foreword to Theory of Graphs by Oystein Ore. [Google print search]
FOUR-VECTOR in the special theory of relativity, from the German Vierervektor used by A. Sommerfeld 1910, in Annalen der Physik und Chemie, ser. 4, 32 (1910), pp. 749-776. The OED finds the English word in 1914: L. Silberstein Theory of Relativity v. 148, “The length, thus defined, of a four-vector may be either real, or purely imaginary, or nil, according as we have . . . a space-like, a time-like, or a singular vector.”
FOURIER INTEGRAL. Fouriersches integral is found using Google print search in 1870 in Ueber eine mit den kugelund Cylinderfunktionen verwandte Function und ihre Andwendung in der Theorie der Electricitatsvertheilung. [James A. Landau]
FOURIER SERIES appears in Björling, "Fourierska serierna," Öfv. af. Förh. Stockh. (1868).
Fourier’s series appears in English in 1859 in On the Stability of the Motion of Saturn’s Rings by J. Clerk Maxwell. [Google print search by James A. Landau]
Fourier series appears in English in 1879 in the article "Function" by Arthur Cayley in the Encyclopaedia Britannica.
FOURIER’s THEOREM is found in English 1833 in The penny cyclopædia: "In the first of the two works, the object of which is the deduction of the mathematical laws of the propagation of heat through solids, Fourier extended the solution of partial differential equations, gave some remarkable views on the solution of equations with an infinite number of terms, expressed the particular value of a function by means of a definite integral containing its general value (whichi is called Fourier’s Theorem), &c." [Google print search]
Isaac Todhunter in the third edition of An Elementary Treatise on the Theory of Equations (1875) refers to "a theorem which English writers usually call Fourier’s theorem, and which French writers connect with the name of Budan as well as with that of Fourier."
FOURIER TRANSFORM is found in English in 1923 in the Proceedings of the Cambridge Philosophical Society [OED].
FOURTH DIMENSION. Nicole Oresme (c. 1323-1382) wrote, "I say that it is not necessary to give a fourth dimension" in Quaestiones super geometriam Euclides [James A. Landau].
In his Algebra (1685) John Wallis wrote, “Nor can our Fansie imagine how there should be a Fourth Local Dimension beyond those Three.”
FRACTAL. According to Franceschetti (p. 357):
In the winter of 1975, while he was preparing the manuscript of his first book, Mandelbrot thought about a name for his shapes. Looking into his son’s Latin dictionary, he came across the adjective fractus, from the verb frangere, meaning “to break.” He decided to name his shapes “fractals.”
Fractal appears in 1975 in Les Objets fractals: Forme, hasard, et dimension by Benoit Mandelbrot (1924- ). The title was translated as Fractals: Form, Chance, and Dimension (1977).
Fractal appears (as an adjective in "the idea of the fractal dimension") in the Nov. 1975 Scientific American [OED].
The OED2 also shows a use of the word by Mandelbrot in Fractals in 1977:
Many important spatial patterns of Nature are either irregular or fragmented to such an extreme degree that..classical geometry..is hardly of any help in describing their form... I hope to show that it is possible in many cases to remedy this absence of geometric representation by using a family of shapes I propose to call fractals - or fractal sets.Johnson (page 155) says the term was coined by Mandelbrot in an article "Intermittent Turbulence and Fractal Dimension" published in 1976.
In The Fractal Geometry of Nature Mandelbrot wrote:
I coined fractal from the Latin adjective fractus. The corresponding Latin verb frangere means "to break:" to create irregular fragments. It is therefore sensible -- and how appropriate for our needs! -- that, in addition to "fragmented" (as infraction or refraction), fractus should also mean "irregular," both meanings being preserved in fragment.According to John Conway, Mandelbrot originally defined fractal to mean "having a possibly fractional dimension." Now it is used most often to describe the self-similarity property that many fractal sets have.The proper pronunciation is frac'tal, the stress being placed as infraction.
The word FRACTION is from the Latin frangere (to break). Some writers called fractions "broken numbers."
In the 12th century Adelard of Bath used minuciae in his Regulae abaci. However in the translation of al-Khowarizmi attributed to Adelard, fractiones is used (Smith vol. 2, page 218).
Johannes Hispalensis in his Liber Algorismi de practica arismetrice used fractiones (Smith vol. 2, page 218).
Fibonacci (1202) generally used fractio.
In English, the word was used by Geoffrey Chaucer (1342-1400) (and spelled "fraccions") about 1391 in A treatise on the Astrolabe [OED].
Broken number is found in 1542 in Ground of Artes (1575) by Robert Recorde: "A Fraction in deede is a broken number" [OED].
Fragment is found in English in in 1579 in Stratioticos by Thomas Digges: "The Numerator of the last Fragment to be reduced."
The terms FRAME and SAMPLING FRAME appear to have entered circulation around 1950. The former is used in F. Yates Sampling Methods for Censuses and Surveys (1949); the latter appears in the title of “The register of electors as a sampling frame” by P.G. Gray, T. Corlett and P. Frankland (1950).
FRÉCHET DIFFERENTIAL. The modern theory of the differential dates from the early 20th century. In “Sur la notion de différentielle” C.R. Acad. Sci. Paris, 152 (1911) pp. 845–847 Maurice Fréchet treated both finite and infinite dimensional cases. He subsequently noticed that his treatment of the finite-dimensional case had been anticipated by G. H. Young: see ibid pages 1050–1051. According to the entry in Encyclopedia of Mathematics Weierstrass had anticipated them both. Fréchet’s name is associated only with the infinite-dimensional case.
See DIFFERENTIAL CALCULUS.
The FREIHEITSSATZ (freedom/independence theorem) of one-relator group theory refers to a theorem proposed by Dehn and proved by W. Magnus “Über discontinuierliche Gruppen mit einer definierenden Relation (Der Freiheitssatz)” Journal für die reine und angewandte Mathematik, 163, (1930), 141-165. In English the expression “the Dehn-Magnus Freiheitssatz” appears in H. Neumann “Generalized Free Products with Amalgamated Subgroups,” American Journal of Mathematics, (1948). Soon the theorem was referred to simply as “the Freiheitssatz.” More recently the expression “a Freiheitssatz” has been applied to any one of a class of similar theorems in group theory and accordingly the original result has become “the classical Freiheitssatz.” See Encyclopaedia of Mathematics. [John Aldrich]
FREQUENCY DISTRIBUTION is found in 1895 in Karl Pearson, " Contributions to the Mathematical Theory of Evolution. II. Skew Variation in Homogeneous Material," Philosophical Transactions of the Royal Society of London (1895) Series A, 186, 343-414: "A method is given of expressing any frequency distribution by a series of differences of inverse factorials with arbitrary constants." (p. 412) [OED].
The term FREQUENTIST (one who believes that the probability of an event should be defined as the limit of its relative frequency in a large number of trials) may occur in 1946 in The New International Year Book: A Compendium of the World’s Progress for the year 1945: “The frequentists are in a hopeless situation.” [Google print search by James A. Landau. It is a snippet view but seems valid.]
Frequentist was used by M. G. Kendall in 1949 in "On the Reconciliation of Theories of Probability," Biometrika, 36, 104: "It might be thought that the differences between the frequentists and the non-frequentists (if I may call them such) are largely due to the differences of the domains which they purport to cover" [OED]. The frequentists Kendall had in mind included John Venn The Logic of Chance and Richard von Mises "Grundlagen der Wahrscheinlichkeitsrechnung," Math. Zeit. 5, (1919) 52-99.
See PROBABILITY.
FRUSTUM first appears in English in 1658 in The Garden of Cyrus or the Quincuncial Lozenge, or Net-work Plantations of the Ancients ... Considered by Sir Thomas Brown: "In the parts thereof [plants] we finde..frustums of Archimedes" [OED].
This word is commonly misspelled as "frustrum" in, for example, Samuel Johnson’s abridged 1843 Edition of his dictionary. The word is spelled correctly in the "Frustum" entry and the "Hydrography" entry in the 1857 Mathematical Dictionary and Cyclopedia of Mathematical Science, but it is misspelled in the entry "Altitude of a Frustrum." The word is misspelled in the 1962 Crescent Dictionary of Mathematics and remains misspelled in the 1989 Webster’s New World Dictionary of Mathematics, which is a revision of the Crescent dictionary. The word is also misspelled in at least three places in The History of Mathematics: An Introduction (1988) by David M. Burton.
FUBINI’S THEOREM on the relationship between a multiple Lebesgue integral and a repeated one was given by Guido Fubini in his “Sugli integrali multipli,” Atti Reale Accad. Lincei Rend. (5), 16, (1907), 608-14. The history of the theorem is recounted in Section 5.3 of T. Hawkins Lebesgue’s Theory of Integration: Its Origins and Development. The first results were obtained by Lebesgue and Beppo Levi and the modern formulation dates from de la Vallée Poussin. See Encyclopedia of Mathematics.
FUCHSIAN FUNCTION. Jules Henri Poincaré introduced the terms groupe Fuchsien and fonction Fuchsienne in his paper “Sur les Fonctions Uniformes qui se reproduisent par des Substitutions Linéaires,” Mathematische Annalen, 19, (1882), 553-564. In the same paper he also introduced function Kleinéenne, groupe Kleinéen, fonctions zétakleinéennes, fonctions zétafuchsiennes, fonctions thétakleinéennes, and fonctions thétafuchsiennes. Klein objected to these terms and in the next volume, 20, 52-53 Poincaré wrote defending them—he wished especially to commemorate the remarkable discoveries of Lazarus Fuchs. See the Encyclopedia of Mathematics entry. [James A. Landau]
According to the DSB, Poincaré used Fuchsian and Kleinean functions for automorphic functions of one complex variable, which he discovered.
According to Wikipedia (2007), Poincaré “named them Fuchsian functions, after the mathematician Lazarus Fuchs, because Fuchs was known for being a good teacher and had researched differential equations and the theory of functions heavily.”
The word FUNCTION first appears in a Latin manuscript "Methodus tangentium inversa, seu de fuctionibus" written by Gottfried Wilhelm Leibniz (1646-1716) in 1673. Leibniz used the word in the non-analytical sense, as a magnitude which performs a special duty. He considered a function in terms of "mathematical job"--the "employee" being just a curve. He apparently conceived of a line doing "something" in a given figura ["aliis linearum in figura data functiones facientium generibus assumtis"]. From the beginning of his manuscript, however, Leibniz demonstrated that he already possessed the idea of function, a term he denominates relatio.
A paper "De linea ex lineis numero infinitis ordinatim..." in the Acta Eruditorum of April 1692, pp. 169-170, signed "O. V. E." but probably written by Leibniz, uses functiones in a sense to denote the various 'offices' which a straight line may fulfil in relation to a curve, viz. its tangent, normal, etc.
In the Acta Eruditorum of July 1694, "Nova Calculi differentialis..." (page 316), Leibniz used the word function almost in its technical sense, defining function as "a part of a straight line which is cut off by straight lines drawn solely by means of a fixed point, and of a point in the curve which is given together with its degree of curvature." The examples given were the ordinate, abscissa, tangent, normal, etc. [Cf. page 150 of Leibniz' "Mathematische Schriften," vol. III, edited by C. I. Gerhardt, Berlin-Halle (Asher-Schmidt), 1849-63.]
In September 1694, Johann Bernoulli wrote in a letter to Leibniz, "quantitatem quomodocunque formatam ex indeterminatis et constantibus," although there is no explicit reference to the Latin term functio. The letter appears in Mathematische Schriften.
On July 5, 1698, Johann Bernoulli, in another letter to Leibniz, for the first time deliberately assigned a specialized use of the term function in the analytical sense, writing "earum [applicatarum] quaecunque functiones per alias applicatas PZ expressae." (Cajori 1919, page 211) [Cf. page 507 of Leibniz' "Mathematische Schriften," vol. III, edited by C. I. Gerhardt, Berlin-Halle (Asher-Schmidt), 1849-63. Also see pages 506-510 and 525-526] At the end of that month, Leibniz replied (p. 526), showing his approval.
Function is found in English in 1779 in Chambers' Cyclopedia: "The term function is used in algebra, for an analytical expression any way compounded of a variable quantity, and of numbers, or constant quantities" [OED].
(Information for this entry was provided by Julio González Cabillón and the OED2.)
The phrase FUNCTION OF x was introduced by Leibniz (Kline, page 340).
The term FUNCTIONAL (noun) is generally attributed to Jacques-Salomon Hadamard (1865-1963). In “Sur quelques points du calcul fonctionnel,” Rendiconti del Circolo matematico di Palermo XXII. (1906) p. 38 M. Fréchet, a student of Hadamard, ascribes the word to Hadamard’s “Sur les opérations fonctionnelles,” (C. R. 1903, p. 351). However, as the OED points out, the term appears only in the phrase opération fonctionnelle. So perhaps Fréchet was responsible for the noun himself. Earlier terms include the “functions of lines” used by Vito Volterra (1860-1940)—see e.g. his Leçons sur les fonctions de lignes, professées à la Sorbonne en 1912.. (Kline, p. 1077)
The term FUNCTIONAL ANALYSIS appears in the title of Paul Lévy’s Leçons de l’analyse fonctionelle (1922). Lévy was writing about FUNCTIONALS but the term functional analysis has been used more often for the study of function spaces, a study that grew out of Hilbert’s work on INTEGRAL EQUATIONS. See Kline chapter 46, Functional Analysis. By 1927 the German reviewing journal Jahrbuch über die Fortschritte der Mathematik was using the category Funktionalalysis and the English term became established in the 1930s. There is a contemporary account of the rise of functional analysis in D. R. Curtiss “Fashions in Mathematics,” American Mathematical Monthly, 44, (Nov., 1937), 559-566.
See the entries HILBERT SPACE and BANACH SPACE. Functional analysis terms are listed under analysis here.
The term FUNCTIONAL CALCULUS is found in 1865 in Chambers’s Encyclopaedia: “The functional calculus is a recent growth of the transcendental analysis. The object of the Differential Calculus (q.v.) is generally to ascertain the changes in functions arising from the continuous and infinitesimal variation of their subject variables. The object of the new functional calculus is, speaking generally, to investigate the forms of functions and their growth, when they are subject to a continuous and infinitesimal change as to form. According to Mr. Price (treatise on the Infinitesimal Calculus), as the differential calculus investigates properties of continuous numbers, so does the new calculus the properties of continuous functions; and as there is an integral calculus of numbers, so there is an inverse calculus of functions. Of the new calculus, the Calculus of Variations (q.v.) may be considered the main branch. It includes, of course, the subject of functional equations.” [James A. Landau]
For functional, Vito Volterra (1860-1940) used the term "functions of other functions," according to Kramer (p. 550). He used "line function," according to the DSB.
FUNCTOR was coined by the German philosopher Rudolf Carnap (1891-1970), who used the word in Logische Syntax der Sprache, published in 1934. For Carnap, a functor was not a kind of mapping, but a function sign - a syntactic entity. In Introduction to Symbolic Logic and its Applications (Dover, 1958) he defined a n-place functor as "any sign whose full expressions (involving n arguments) are not sentences". This definition implies that a functor must stand before its argument-expressions, so that the sign +, for example, is not a functor when used as an infix sign ^ although it has the same logical character as a functor. According to him, the function designated by a functor is the "intension" of that functor, while its "extension" is the "value-distribution" of the function.
As used in category theory, functor was introduced by Samuel Eilenberg and Saunders Mac Lane in "Natural Isomorphisms in Group Theory," Proceedings of the National Academy of Sciences, 28, (1942), pp. 537-543. They borrowed the term from Carnap’s Logische Syntax der Sprache. In his Categories for the Working Mathematician (1972) Mac Lane says (pp. 29-30):
Categories, functors, and natural transformations were discovered by Eilenberg-Mac Lane (...) Now the discovery of ideas as general as these is chiefly the willingness to make a brash or speculative abstraction, in this case supported by the pleasure of purloining words from the philosophers: "Category" from Aristotle and Kant, "Functor" from Carnap (...).In A History of Algebraic and Differential Topology 1900-1960 Jean Dieudonné wrote (p. 96):
Perhaps the custom they [S. Eilenberg and S. Mac Lane] had adopted of systematically using notations such as (...) for the various groups they defined in their 1942 paper, suggested to them that they were defining each time a kind of "function" which assigned a commutative group to an arbitrary commutative group (or to a pair of such groups) according to a fixed rule. Perhaps to avoid speaking of the "paradoxical" "set of all commutative groups", they coined the word "functor" for this kind of correspondence; (...)
This entry was contributed by Carlos César de Araújo. See the entry CATEGORY.
FUNDAMENTAL EQUATION is found in 1808 in A New and Complete System of Arithmetick, Composed for the Use of the Citizens of the United States by Nicolas Pike. An algebra problem requires two linear equations and the author refers to each of them as a fundamental equation. [Google print search by James A. Landau]
This term was used by Leopold Alexander Pars (1896-1985) for the theorem of Lagrange.
The term FUNDAMENTAL FUNCTIONS (meaning eigenfunctions) is due to Poincaré, according to the University of St. Andrews website.
The FUNDAMENTAL GROUP (“le groupe fondamental”) of algebraic topology was introduced by J. H. Poincaré in Section 12 of his “Analysis Situs,” Journal de l’École Polytechnique, 1, (1892) 1-121, according to Jean Dieudonné A History of Algebraic and Differential Topology, 1900-1960, p. 23. The English term appears in O. Veblen & J. W. Alexander “Manifolds of N Dimensions,” Annals of Mathematics, 14, (1912 - 1913), p. 163. See also MathWorld.
See TOPOLOGY.
FUNDAMENTAL SYSTEM. According to the DSB, Immanuel Lazarus Fuchs (1833-1902) "introduced the term 'fundamental system' to describe n linearly independent solutions of the linear differential equation L(u) = 0."
FUNDAMENTAL THEOREM. Perhaps the earliest use of the term fundamental theorem is by Gauss in the sense of the FUNDAMENTAL THEOREM OF QUADRATIC RESIDUES.
The term FUNDAMENTAL THEOREM OF ALGEBRA "appears to have been introduced by Gauss" (Smith, 1929, and Burton, page 512). However, Grattan-Guinness (1997, p. 412) disagrees, "The modern name, 'the fundamental theorem of algebra', seems to have come in late in the 19th century; Gauss himself never used it."
Fundamental theorem of algebra appears in English in 1887 in “A New Method in Analytic Geometry” by William E. Story in American Journal of Mathematics: “...the fundamental theorem of algebra, briefly stated: every equation has a root.” [Google print search, James A. Landau]
FUNDAMENTAL THEOREM OF ARITHMETIC is found in 1915 in An Arithmetical Theory of Certain Numerical Functions by Eric Temple Bell: “Within N there is a denumerable assemblage, P, of elements, which are such that with respect to elements of P every element of N satisfies the fundamental theorem of arithmetic, viz., every element of N may be represented as a product of powers of distinct members of P in one way only.” [Google print search by James A. Landau]
The term appears with another meaning in 1895 in the Century Dictionary: "the proposition that any lot of things the count of which in any order can be terminated is such that the count in every order can be terminated, and ends with the same number."
FUNDAMENTAL THEOREM OF CALCULUS. Fundamental theorem for the Method of Variations is found in German in 1805 here. [Google print search by James A. Landau]
A fundamental theorem of the Calculus of Variations is found in 1861 in A History of the Progress of the Calculus of Variations During the Nineteenth Century by I. Todhunter. [Google print search by James A. Landau]
In 1902 An Introduction to the Summation of Differences of a Function by Benjamin Feland Groat has: "The fundamental theorem of the integral calculus puts into mathematical language a rule for finding the limit of any sum, of the kind considered, provided an identity of the right form can be found; and the rules an formulae of the integral calculus afford a method for the discovery of the essential form of the identity when it exists." [Google print search]
Fundamental theorem of the calculus is found in 1934 in Fourier Transforms in the Complex Domain by Norbert Wiener. [Google print search]
Fundamental theorem of calculus is found in 1942 in Calculus by George Eulas Foster Sherwood and Angus Ellis Taylor. [Google print search by James A. Landau]
According to Joe Johnson, Andre Weil referred to the "so-called fundamental theorem of calculus" in a scathing book review of Hoffmann’s work on Leibniz in Paris. Weil regarded the rule for change of variables as the truly fundamental theorem whose discovery makes the difference between pre-calculus efforts of Mercator and others and the real thing.
The term second fundamental theorem of calculus is found in 1959 in A Course in Mathematical Analysis by Norman B. Haaser. [Google print search]
FUNDAMENTAL THEOREM OF QUADRATIC RESIDUES. In his Disquisitiones arithmeticae Gauss wrote:
Quia omnia fere quae de residuis quadraticis dici possunt, huic theoremati innituntur, denominatio theorematis fundamentalis, qua in sequentibus utemur, haud absona erit. [Since almost everything that can be said about quadratic residues depends on this theorem, the term fundamental theorem, which we will use from now on, should be acceptable.]
Eisenstein used the term Fundamental Theorem of Quadratic Residues.
[James A. Landau]
FUZZY had been in the language since the 17th century (OED) but it only became a technical term in the 1960s. Lotfi A. Zadeh (1921- ) explained why he adopted it in an interview with Betty Blair:
I coined the word "fuzzy" because I felt it most accurately described what was going on in the theory. I could have chosen another term that would have been more "respectable" with less pejorative connotations. I had thought about "soft," but that really didn't describe accurately what I had in mind. Nor did "unsharp," "blurred," or "elastic." In the end, I couldn't think of anything more accurate so I settled on "fuzzy".
The OED gives a reference to 1964, to L. A. Zadeh et al. Memorandum (Rand Corporation) RM-4307-PR 1 “The notion of a ‘fuzzy’ set..extends the concept of membership in a set to situations in which there are many, possibly a continuum of, grades of membership.”
Zadeh’s early publications on fuzziness include "Fuzzy sets". Information and Control 8, (1965), 338-353 here and “Probability measures of fuzzy events,” Journal of Mathematical Analysis and Applications, 23, (1968), 421-427. here
Fuzzy logic appears in 1969 in P.N. Marinos “Fuzzy Logic and its Application to Switching Systems,” IEEE Transactions on Computers, 18, 348/2: “In the digital field, pattern recognitions and classification are .. potential users of fuzzy logic” (OED).
Fuzzy in a slightly different technical sense appears in 1976 in Numbers and Games by J. H. Conway: “We say that G and H are confused or that G is fuzzy against H.”
FUZZY MATH. “Exercise for Fuzzy Math Fans” appears in the European Stars and Stripes on Jan. 8, 1967.
On May 26, 1997, a column by in U. S. News and World Report by John Leo has: “Now 'Deep Thoughts' are available on greeting cards, including one that pokes fun at the fuzzy new math in the schools.”
Fuzzy math appears on June 11, 1997, in the Wall Street Journal in the headline “President Clinton’s Mandate for Fuzzy Math.” In the article, Lynne V. Cheney wrote, “Sometimes called 'whole math' or 'fuzzy math,' this latest project of the nation’s colleges of education has some formidable opponents.”
In a Presidential debate on Oct. 3, 2000, George W. Bush said, "Look this is the man who’s got great numbers. He talks about numbers. I'm beginning to think not only did he invent the Internet, but he invented the calculator. It’s fuzzy math."