Earliest Known Uses of Some of the Words of Mathematics (C)

Last revision: June 25, 2017

CALCULUS. In Latin calculus means "pebble." It is the diminutive of calx, meaning a piece of limestone. The counters of a Roman abacus were originally made of stone and called calculi. (Smith vol. 2, page 165).

In Latin, persons who did counting were called calculi. Teachers of calculation were known as calculones if slaves, but calculatores or numerarii if of good family (Smith vol. 2, page 166).

The Romans used calculos subducere for "to calculate."

In Late Latin calculare means "to calculate." This word is found in the works of the poet Aurelius Clemens Prudentius, who lived in Spain c. 400 (Smith vol. 2, page 166).

Calculus in English, defined as a system or method of calculating, is dated 1666 in MWCD10, presumably from Monsieur Hevelius’s Calculation of the Late Solar Eclipse’s Quantity, Duration, &c (in Number 21 Philosophical Transactions, Vol. 1, (1665 - 1666), p. 369. In its early days the Philosophical Transactions published articles in Latin as well as in English and calculus often appeared in the Latin articles.

The earliest citation in the OED2 for calculus in the sense of a method of calculating, is in 1672 in Extract of a Letter of Monsieur Hevelius from Dantzick Written to the Publisher in Latin, March 9. (st. Nov.) 1672; Giving Some Accompt of a New Comet, Lately Seen in That Country: Englished as Followeth Philosophical Transactions Vol. VII, p. 4017: "I cannot yet reduce my Observations to a calculus."

The restricted meaning of calculus, meaning differential and integral calculus, is due to Leibniz.

A use by Leibniz of the term appears in the title of a manuscript Elementa Calculi Novi pro differentiis et summis, tangentibus et quadraturis, maximis et minimis, dimensionibus linearum, superficierum, solidorum, allisque communem calculum transcendentibus [The Elements of a New Calculus for Differences and Sums, Tangents and Quadratures, maxima and minima, the measurement of lines, surfaces and solids, and other things which transcend the usual sort of calculus]. The manuscript is undated, but appears to have been compiled sometime prior to 1680 (Scott, page 157).

Newton did not originally use the term, preferring method of fluxions (Maor, p. 75). He used the term Calculus differentialis in a memorandum written in 1691 which can be found in The Collected Correspondence of Isaac Newton III page 191.

Webster’s dictionary of 1828 has the following definitions for calculus, suggesting the older meaning of simply "a method of calculating" was already obsolete:

1. Stony; gritty; hard like stone; as a calculous concretion.
2. In mathematics; Differential calculus, is the arithmetic of the infinitely small differences of variable quantities; the method of differencing quantities, or of finding an infinitely small quantity, which, being taken infinite times, shall be equal to a given quantity. This coincides with the doctrine of fluxions.
3. Exponential calculus, is a method of differencing exponential quantities; or of finding and summing up the differentials or moments of exponential quantities; or at least of bringing them to geometrical constructions.
4. Integral calculus, is a method of integrating or summing u moments or differential quantities; the inverse of the differential calculus.
5. Literal calculus, is specious arithmetic or algebra.

In older uses, the word calculus, referring to differential and integral calculus, was normally preceded by the word the. Listed below are some early uses of the word without the, although in some of these citations the word calculus may be in the older sense of “a method of calculating,” and they properly do not belong here.

The 1796 edition of the Encyclopaedia Britannica has, in a discussion of fluid resistance in the article “Resistance,” the following:

It must be acknowledged, that the results of this theory agree but ill with experiment, and that, in the way in which it has been zealously prosecuted by subsequent mathematicians. It proceeds on principles or assumptions which are not only gratuitous, but even false. But it affords such a beautiful application of geometry and calculus, that mathematicians have been as it were fascinated by it, and have published systems so elegant and extensively applicable, that one cannot help lamenting that the foundation is so flimsy.

In 1806 The Monthly Review, Or, Literary Journal by Ralph Griffiths, G. E. Griffiths has “The whole of this analysis of the mechanism of Saturn’s ring is of the most intricate kind, and is carried on by the author by calculus alone, so as not to be instructive to any but very learned and expert analysts.” This citation is from a review of Elements of Mechanical Philosophy by John Robinson.

In 1815 A Philosophical and Mathematical Dictionary by Hutton has, in the entry for transcendental, the following:

He also shows how it may be demonstrated without calculus, that an algebraic quadratrix for the circle or hyperbola is impossible: for if such a quadratrix could be found, it would follow, that by means of it .any anale, ratio, or logarithm, might be divided in a given proportion of one right line to another, and this by one universal construction : and consequently the problem of the section of an angle, or the invention of any number of mean proportionals, would be of a certain finite degree.

In 1819 A Treatise on Plane and Spherical Trigonometry by Robert Woodhouse has:

This completes the solution of the brachystochrone, of which there are six cases, [see pp. 113,122, 141, 145, 147, 149.] and this curve which first called the attention of mathematicians to the connected doctrine and calculus, has been also the object of their latest researches.

In 1857 the Indiana School Journal published by the Indiana State Teachers Association has “ ... plain that any one who has a moderate knowledge of Calculus may comprehend it: Let AP represent the required curve, the body commencing to fall from A, ...” and “[This is a fine problem for solution by calculus. It can also be solved very beautifully by arithmetic. We hope those who understand calculus, ...” and “Robinson, solved it by calculus, and deduced the interesting fact that the perpendicular must vary as rapidly as tie smaller segment of the base, ... .” The journal elsewhere refers to “the Integral Calculus.”

John Aldrich and James A. Landau contributed to this entry. See also DIFFERENTIAL CALCULUS, INTEGRAL CALCULUS. For a list of entries associated with the differential calculus see here.

The term CALCULUS OF DERIVATIONS was coined by Louis François Antoine Arbogast, according to the Mathematical Dictionary and Cyclopedia of Mathematical Science. Arbogast is the author of Du Calcul des Dérivations (1800).

CALCULUS OF FINITE DIFFERENCES. The first systematic account of the calculus of finite differences is found in Brooke Taylor’s Methodus incrementorum directa et inversa of 1715. The corresponding English phrase appears in 1763 in the title of W. Emerson’s The Method of Increments. Important contributors to the subject included Euler and Lagrange. Lagrange used the term “différence finie” and the symbol Δu for “la différence première finie du u” in his “Sur une nouvelle espèce de calcul relatif à la différentiation et à l'intégration des quantités variables,” (1772) (Oeuvres de Lagrange tome 3 pp. 441ff.).

Calculus of finite differences appears in English in 1802 in a review of J. E. Montucla, “A History of Mathematics,” in The Critical Review; or, Annals of Literature; Extended & Improved: “Several new branches of analysis having arisen out of the foregoing, the author treats of them to such extent as the nature of his work will permit; such as the calculus of finite differences; that of circular, logarithmic, and imaginary quantities; the methods of limits, of analytic functions, of variations, of partial differentials, of infinite series, of eliminations, of interpolations, of continued fractions, &c.” [Google print search, James A. Landau]

(Based on Cajori A History of Mathematical Notations. vol. II pp. 263-7 and Encyclopaedia of Mathematics.)

The term CALCULUS OF VARIATIONS was introduced by Leonhard Euler in a paper, "Elementa Calculi Variationum," presented to the Berlin Academy in 1756 and published in 1766 (Kline, page 583; DSB; Cajori 1919, page 251). Lagrange used the term method of variations in a letter to Euler in August 1755 (Kline).

Calculus of variations is found in English in 1800 in what what appears to be a review of a book by Lacroix on “Differencial and Integral Calculus” in The Monthly Review; or Literary Journal, Enlarged From May to August, inclusive, M,DCCC: “The calculus of variations originated from certain problems concerning the maxima and minima of quantities having been proposed; by John Bernoulli, to the mathematicians of Europe. Such a problem was that in which is was required to find, of all curves passing through two fixed points, and situated in the same vertical plane, that one down which a body would descend from the highest to the lowest point in the least time possible.” [Google print search, James A. Landau]

CANONICAL CORRELATION was introduced by H. Hotelling in "Relations between Two Sets of Variates," Biometrika, 28, (1936), 321-377. Section 2 of the paper is called "Canonical Variates and Canonical Correlation." In a footnote on p. 325 Hotelling remarks that "The word ‘canonical’ is used in the algebraic theory of invariants with a meaning consistent with that of this paper." David (2001)

The term CANONICAL FORM is due to Hermite (Smith, 1906).

Canonical form is found in 1851 in the title “Sketch of a Memoir on Elimination, Transformation, and Canonical Forms,” by James Joseph Sylvester (1814-1897), Cambridge and Dublin Mathematical Journal 6 (1851). He wrote, on page 193, “I now proceed to the consideration of the more peculiar branch of my inquiry, which is as to the mode of reducing Algebraical Functions to their simplest and most symmetrical, or as my admirable friend M. Hermite well proposes to call them, their Canonical forms.” [James A. Landau]

CANTOR SET or CANTOR’S TERNARY SET. Georg Cantor introduced his ternary set in a note to the Grundlagen einer allgemeinen Mannichfaltigkeitslehre of 1883, writes J. W. Dauben in Georg Cantor (1979, p. 329, n. 43). See the Encyclopaedia of Mathematics entry.

CANTOR’S DIAGONAL METHOD. According to Kline (p. 997), Georg Cantor used his diagonal method in his second proof that the real numbers are uncountable. This is contained in his “Ueber eine elementare Frage der Mannigfaltigketislehre,” Jahresbericht der Deutschen Mathematiker-Vereinigung, 1, (1890/91), 75-78. For text and English translation see here.

CARDINAL. Glareanus recognized the metaphor between cardinal numbers and Cardinal, a prince of the church, writing in Latin in 1538.

The earliest citation in the OED2 is by Richard Percival in 1591 in Bibliotheca Hispanica: "The numerals are either Cardinall, that is, principall, vpon which the rest depend, etc."

CARDIOID was first used by Johann Castillon (Giovanni Francesco Melchior Salvemini) (1708-1791) in "De curva cardiode" in the Philosophical Transactions of the Royal Society (1741) [Julio González Cabillón and DSB].

CARMICHAEL NUMBER appears in H. J. A. Duparc, “On Carmichael numbers,” Simon Stevin 29, 21-24 (1952). The existence of such numbers was noted by R. D. Carmichael “Note on a New Number Theory Function.” Bulletin of the American Mathematical Society, 16, (1910), 232-238. See MathWorld.

CARRY (process used in addition). According to Smith (vol. 2, page 93), the "popularity of the word 'carry' in English is largely due to Hodder (3d ed., 1664)."

CARTESIAN, from Cartesius the Latin name for the mathematician and philosopher René Descartes (1596-1650), appears in several expressions. The mathematical ones usually relate to La Géométrie (1637). The terms can be misleading, for as Boyer remarks:

Cartesian geometry now is synonymous with analytic geometry, but the fundamental purpose of Descartes was far removed from that of modern textbooks. The theme is set by the opening sentence: "Any problem in geometry can easily be reduced to such terms that a knowledge of the lengths of certain lines is sufficient for its construction." As this statement indicates, the goal is generally a geometric construction, and not necessarily the reduction of geometry to algebra. The work of Descartes far too often is described simply as the application of algebra to geometry, whereas actually it could be characterized equally well as the translation of the algebraic operations into the language of geometry.

Cartesian geometry was used by Jean Bernoulli "as early as 1692," according to Boyer (p. 484).

Cartesian coordinates. Hamilton used Cartesian method of coordinates in a paper of 1844 [James A. Landau].

Cartesian coordinates is found (with the initial letter of Cartesian capitalized) in 1868 in “Mathematical Questions, with their Solutions,” Educational Times, Volume IX. [Google print search, James A. Landau]

Cartesian plane. A JSTOR search found the phrase in 1904 in H. A. Converse "On a System of Hypocycloids of Class Three Inscribed to a Given 3-Line, and Some Curves Connected with it," Annals of Mathematics, 2nd Ser., 5, 105-139.

Cartesian product. This set theoretic term entered circulation in the 1930s. Previously product (Produkt) was the established term: see, e.g. Felix Hausdorff Grundzüge der Mengenlehre (1914, p. 37)) Kuratowski wrote produit for intersection and produit cartésien for the former product (Topologie I (1934, p. 7)). Hausdorff had used Durchschnitt for intersection, so there was no danger of confusion.

In English a JSTOR search found F. J. Murray "Linear Transformations Between Hilbert Spaces and the Application of This Theory to Linear Partial Differential Equations," Transactions of the American Mathematical Society, 37, (1935), 301-338.

Boyer (p. 346) considers the term "Cartesian product" an anachronism because Descartes did not think of his coordinates as number pairs.

CASTING OUT NINES. Fibonacci called the excess of nines the pensa or portio of the number (Smith vol. 1, page 153).

Liber abaci (1202, revised 1228) has:

Uerum si prescriptam diuisionem per pensam nouenarii probare uoluerit accipiat pensam de 13976 que sunt 8 et seruet eam ex parte. Et iterum accipiat pensam exeuntis numeri, scilicet de 607, que sunt 4 et multiplicet eam per pensam de 23, que sunt 5, erunt 20; de quibus accipiat pensam, que sunt 2 et addat eam cum 15 que sunt super uirgulam de 23, erunt 17, quorum pensa sunt 8, sicuti superius ex parte seruauimus.

A phrase from the Treviso Arithmetic (1478) is translated "If you wish to check the sum by casting out nines...."

Pacioli (1494) spoke of it as "corrente mercatoria e presta" (Smith vol. 1, page 153).

Christopher Clavius used the term "Probatio additiones per 9" in Epitome Arithmeticae Practicae (1607, Köln, p. 16-17), according to Albrecht Heeffer.

“Casting away nines” is found in 1701 in A Compleat Body of Arithmetick, in Four Books by Samuel Jeake: “the proof af all sorts of Multiplication may be had, either by Addition, Casting away Nines, or Division.” [Google print search, James A. Landau]

"Casting out the nines" is found in the first edition of the Encyclopaedia Britannica (1768-1771) in the article, "Arithmetick."

CATALAN NUMBERS. The phrases “Catalan’s sequence 1, 2, 5, 14, 42, 132,...” and “Catalan’s numbers” appear in E. T. Bell, “The Iterated Exponential Integers,” Annals of Mathematics, Second Series, Vol. 39, No. 3, pp. 539-557, July 1938.

John Riordan refers to “the Catalan numbers C_{2n,n}/(n+1)” in his review (MR0024411) of Theodore Motzkin’s paper, “Relations between hypersurface cross ratios...,” Bull. Amer. Math. Soc., Vol 54, pp. 352–360, 1948. [David Callan]

CATALECTICANT. “Beginning in the 1840s and almost literally until the day he died, [Sylvester] composed his own original verses in English, Latin and Italian and, in 1870, published a book on what he deemed to be The Laws of Verse,” writes Karen Hunger Parshall, James Joseph Sylvester (2006, p. 7). Sylvester’s interest in poetry is reflected in the family of terms he created around the word catalectic. According to the OED, the word—in English from 1589—describes verse “lacking a syllable at the end or ending in an incomplete foot.”

Sylvester used catalectic as an algebraic term in “An Essay on Canonical Forms” (1851). The OED quotes the phrase, “The theory of the catalectic forms of functions of the higher degrees of two variables.” (from p. 211 of the reprint in Sylvester’s Collected Papers vol. 1.)

Sylvester used his new word catalecticant in “On the principles of the calculus of forms,” Cambridge and Dublin Mathematical Journal 7 (1852), 52-97, explaining in a footnote:

But the catalecticant of the biquadratic function of x, y was first brought into notice as an invariant by Mr Boole; and the discriminant of the quadratic function of x, y is identical with its catalecticant, as also with its Hessian. Meicatalecticizant would more completely express the meaning of that which, for the sake of brevity, I denominate the catalecticant.

This footnote appears on p. 293 of vol. 1 of the Collected Papers.

Bruce Reznick, who provided this quotation, writes, “Sylvester may appear a little pompous to us, but there is a reason for his language: a ‘catalectic’ verse is one in which the last line is missing a foot. A general homogeneous polynomial p(x,y) of degree 2k can be written as a sum of k+1 linear polynomials raised to the 2k-th power . . . unless its catalecticant vanishes, in which case it needs k linear polynomials, or fewer.”

In a letter to Thomas Archer Hirst dated Dec. 19, 1862, Sylvester reflected on the word catalecticant:

On further reflexion I retract my opinion expressed yesterday evening and recommend the continuance [illegible] of the word ‘Catalecticant.’ This sort of invariant is so important and stands in such close relation to the Canonizant that we cannot afford to let it go unnamed and as this name has been used by Cayley as well as myself it may as well remain. ... I took the Idea of the name from the Iambicus Trimeter Catalecticus.”

Sylvester also used the word meiocatalecticizant.

The word meicatalecticizant which Sylvester had rejected for its lack of “brevity” and which probably subsequently disappeared was revived by Reznick in his monograph Sums of Even Powers of Real Linear Forms, Memoir of the American Mathematical Society, No. 463 (1992).

CATASTROPHE THEORY is found in Thomas F. Banchoff, "Polyhedral catastrophe theory. I: Maps of the line to the line," Dynamical Syst., Proc. Sympos. Univ. Bahia, Salvador 1971, 7-21 (1973).

CATEGORICAL (AXIOM SYSTEM). This term was suggested by John Dewey (1859-1952) to Oswald Veblen (1880-1960) and introduced by the latter in his A system of axioms for geometry, Trans. Amer. Math. Soc. 5 (1904), 343-384, p. 346. Since then, the term as well as the notion itself has been attributed to Veblen. Nonetheless, the first proof of categoricity is due to Dedekind: in his Was sind und Was sollen die Zahlen? (1887) it was in fact proved that the now universally called "Peano axioms" are categorical - any two models (or "realizations") of them are isomorphic. In Dedekind’s words:

132. Theorem. All simply infinite systems are similar to the number-series N and consequently (...) to one another.

Instead of "categorical", the term "complete" is sometimes used, chiefly in older texts. The influence, in this case, comes from Hilbert’s Vollständigkeitsaxiom ("completeness axiom") in his Über den Zahlbegriff (1900). Other names that were proposed for this concept are "monomorphic" (for categorical and consistent in Carnap’s Introduction to symbolic logic, 1954) and "univalent" (Bourbaki), but these did not attain popularity. (It goes without saying that there is no connection with "Baire category", "category theory" etc.) The concept was somewhat shaken when Thoralf Skolem discovered (1922) that first-order set theory is not categorical. Facts like this have caused some confusion among mathematicians. Thus in his The Loss of Certainty (1980, p. 271) Morris Kline wrote:

Older texts did "prove" that the basic systems were categorical; (...) But the "proofs" were loose (...) No set of axioms is categorical, despite "proofs" by Hilbert and others.

The fact is, there are two distinct notions of axiomatics and, with respect to one, the older texts did prove categoricity and not merely "prove".

CATEGORY (of a set). See BAIRE CATEGORY.

CATEGORY (theory). The term category was introduced by Samuel Eilenberg; Saunders MacLane “General Theory of Natural Equivalences,” Transactions of the American Mathematical Society, Vol. 58, No. 2. (Sep., 1945), pp. 231-294. See the entries in the Encyclopedia of Mathematics and the Stanford Encyclopedia of Philosophy.

CATENARY. According to E. H. Lockwood (1961) and the University of St. Andrews website, this term was first used (in Latin as catenaria) by Christiaan Huygens (1629-1695) in a letter to Leibniz dated November 18, 1690.

According to Schwartzman (page 41) and Smith (vol. 2, page 327), the term was coined by Leibniz.

Maor (p. 142) shows a drawing by Leibniz dated 1690 which Leibniz labeled "G. G. L. de Linea Catenaria."

Huygens wrote "Solutio problematis de linea catenaria" in the Acta Eruditorum in 1691.

In a paper in the Acta Eruditorum of June 1691, Leibniz wrote (in translation), "The problem of the catenary curve, or funicular curve, is interesting for two reasons. . ."

Catenary is found in English in 1725 in Lexicon Technicum: Or, An Universal English Dictionary of ARTS and SCIENCES: Fourth Edition Volume I:

CATENARIA, is the Curve Line which a Rope hanging freely between two Points of Suspension forms itself into. What the Nature of this Curve is, was enquired amongst the Geometricians in Galileo’s time, but I don’t find any thing was done towards a Discovery till in the Year 1690, James Bermoulli published it as a Problem; which about two Months after, Leibnitz declared he had found out, and would communicate with the Year: In December, 1690, John the Brother of James Bernoulli communicated an Investigation of it to the Editors of the Acta Eruditorium, which was publish’d afterwards June, 1691. This Catenary or Funicular he saith he found not to be truly Geometrical, but of the Mechanical Kind, because its Nature cannot be expressed by a determinate Algebraick Equation; but Leibnitz gives its Construction Geometrically.

In 1727-41, Ephraim Chambers' Cyclopedia or Universal Dictionary of Arts and Sciences uses the Latin form catenaria in the article on the tractrix [OED].

The OED shows a use of catenarian curve in English in 1751.

The 1771 edition of the Encyclopaedia Britannica uses the Latin form catenaria:

CATENARIA, in the higher geometry, the name of a curve line formed by a rope hanging freely from two points of suspension, whether the points be horizontal or not. See FLUXIONS.

In a letter to Thomas Jefferson dated Sept. 15, 1788, Thomas Paine, discussing the design of a bridge, used the term catenarian arch:

Whether I shall set off a catenarian Arch or an Arch of a Circle I have not yet determined, but I mean to set off both and take my choice. There is one objection against a Catenarian Arch, which is, that the Iron tubes being all cast in one form will not exactly fit every part of it. An Arch of a Circle may be sett off to any extent by calculating the Ordinates, at equal distances on the diameter. In this case, the Radius will always be the Hypothenuse, the portion of the diameter be the Base, and the Ordinate the perpendicular or the Ordinate may be found by Trigonometry in which the Base, the Hypothenuse and right angle will be always given.

In a reply to Paine dated Dec. 23, 1788, Thomas Jefferson used the word catenary:

You hesitate between the catenary, and portion of a circle. I have lately received from Italy a treatise on the equilibrium of arches by the Abbé Mascheroni. It appears to be a very scientifical work. I have not yet had time to engage in it, but I find that the conclusions of his demonstrations are that 'every part of the Catenary is in perfect equilibrium.'

CATHETUS. Nicolas Chuquet (d. around 1500), writing in French, used the word cathète (DSB).

Cathetus occurs in English in 1571 in A Geometricall Practise named Pantometria by Thomas Digges (1546?-1595) (although it is spelled Kathetus).

Cathetus is found in English in the Appendix to the 1618 edition of Edward Wright’s translation of Napier’s Descriptio. The writer of the Appendix is anonymous, but may have been Oughtred.

The terms CAUCHY CONVERGENCE and CAUCHY SEQUENCE derive from the work of Maurice Fréchet (1878-1973) (Katz). In "Sur quelques points du calcul fonctionnel," Rendiconti del Circolo matematico di Palermo, 22, (1906) p. 23 Fréchet writes of a sequence of elements of a set satisfying "les conditions de Cauchy" although he gives no reference to Cauchy. A JSTOR search found Cauchy sequence in K. W. Lamson "A General Implicit Function Theorem with an Application to Problems of Relative Minima," American Journal of Mathematics, 42, (1920), p. 245.

CAUCHY CONVERGENCE TEST. Cauchy’s integral test is found in 1893 in A Treatise on the Theory of Functions by James Harkness and Frank Morley: "Cauchy’s integral test for the convergence of simple series can be extended to double series."

Cauchy’s condition of convergence is found in 1915 in an English translation of Contributions to the Founding of the Theory of Transfinite Numbers By Georg Cantor: “a sequence of numbers satisfying Cauchy’s condition of convergence.” [Google print search, James A. Landau]

Cauchy’s convergence test and Cauchy test appear in 1937 in Differential and Integral Calculus, 2nd. ed. by R. Courant. Courant writes that the test is also called the general principle of convergence [James A. Landau].

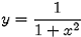
and variants of it have been studied for around 300 years in a variety of contexts. In its oldest form it is known as the WITCH OF AGNESI. The history of the use of the function in probability is traced in S. M. Stigler “Cauchy and the Witch of Agnesi” (in Stigler (1999)). The function was introduced by Poisson in 1824 in his “Sur la probabilité des résultats moyens des observations,” Connaissance des Temps pour l’an 1827, 273-302 and the association is duly noted in Bertand’s Calcul des Probabilités (1889, p. 257). However, the name most often associated with the function is that of Cauchy who reintroduced the function in 1853 in his “Sur les résultats moyens d’observations de même nature, et sur les résultats les plus probables,” Comptes Rendus de l'Académie des Sciences, 37, (1853), 198-206. The name, “la loi de Cauchy,” appears in Lévy’s Calcul des Probabilités (1925, p. 179); Lévy had an interest in the law as one of the STABLE LAWS. In the English literature the name “Cauchy distribution” entered circulation in the 1930s: see e.g. B. O. Koopman’s “On Distributions Admitting a Sufficient Statistic,” Transactions of the American Mathematical Society, 39, (1936), pp. 399-409. Earlier writers had other ways of referring to the distribution; thus to R. A. Fisher (Mathematical Foundations of Theoretical Statistics (1922), pp. 321-2) it was a Pearson “Type VII” distribution; for this terminology see the entry PEARSON CURVES.

A version of the function is used in optics where it is called the LORENTZIAN FUNCTION after H. A. Lorentz “The width of spectral lines,” Proc. Acad. Sci. Amsterdam, 18, (1915), 134-150; see MathWorld Lorentzian Function. In particle physics there is another version called the BREIT-WIGNER DISTRIBUTION after G. Breit & E. P. Wigner “Capture of slow neutrons,” Physical Review, 49, (1936), 519-544. See Chronology of Milestone Events in Particle Physics and Wikipedia Relativistic Breit–Wigner distribution. [This entry was contributed by John Aldrich.]

CAUCHY-RIEMANN EQUATIONS. These equations had been studied by d’Alembert and Euler in the eighteenth century but they were made the basis of a theory of complex analysis in the nineteenth century by Cauchy and Riemann. The relevant works are A. L. Cauchy, "Mémoire sur les intégrales définies," (1814  but published in 1827) Oeuvres Ser. 1, 1 pp. 319-506 and B. F. Riemann  "Grundlagen für eine allgemeine Theorie der Funktionen einer veränderlichen komplexen Grösse" (1851) Werke p. 1. See Kline chapter 27 and the Encyclopaedia of Mathematics article Cauchy-Riemann conditions. [John Aldrich]

CAUCHY’S THEOREM appears in 1868 in Genocchi, "Intorno ad un teorema di Cauchy," Brioschi Ann.

The term also appears in the title "Sur un théorème de Cauchy présenté par M. Hermite" (1868).

Cauchy’s theorem appears in the third edition of An Elementary Treatise on the Theory of Equations (1875) by Isaac Todhunter.

CAUCHY-SCHWARZ INEQUALITY. The term l’inégalité de Schwarz is found in an 1896 paper by Poincare in Acta Mathematica 20.

Cauchy-Schwarz inequality was used in English by Hardy and Littlewood in a paper in Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, 1920, p. 39.

The history of the contributing inequalities is given in Inequalities by G. H. Hardy, J. E. Littlewood and G. Polya (1934): the inequality for sums is due to A. L. Cauchy in 1821 (p. 373 of Oeuvres 2, III) and the inequality for integrals to H. A. Schwarz (p. 251 of his Gesammelte mathematische Abhandlungen, Vol. 1.), “although it seems to have been stated first by Buniakovsky” in 1859. In Russia the integral version is known as the Buniakovskii inequality.

The name "Cauchy-Schwarz" is often misprinted as "Cauchy-Schwartz" suggesting, perhaps, a spurious connection to one of the twentieth century mathematicians L. and J. T. Schwartz.

John Aldrich, Jan Peter Schäfermeyer, and James A. Landau contributed to this entry.

CAYLEY-HAMILTON THEOREM. This was stated in 1858 by Arthur Cayley (1821-1895) "A Memoir on the Theory of Matrices" Coll Math Papers, I, 475-96. Cayley "verified" it for the case of 3 dimensions, remarking "I have not thought it necessary to undertake the labour of a formal proof of the theorem in the general case of a matrix of any degree." (p. 483). Later it was realised that William Rowan Hamilton (1805-1865) had proved the theorem for quaternions in the Lectures on Quaternions (1853 p. 566). In Maxime Bôcher’s Introduction to higher algebra (1907, p. 296) the theorem is embodied in the Hamilton-Cayley equation. H.W. Turnbull The Theory of Determinants, Matrices, and Invariants (1929) refers to the Cayley-Hamilton theorem.

(Based on Kline pp. 807-8.)

CAYLEY’S SEXTIC was named by R. C. Archibald, "who attempted to classify curves in a paper published in Strasbourg in 1900," according to the St. Andrews University website.

Mr. Cayley’s sextic is found in September 1883 in American Journal of Mathematics, Volume VI, Number 1: “Mr. Cayley’s sextic involves a cyclic function of the roots, namely, φ = r₁r₂ .... ” [Google print search, James A. Landau]

CAYLEY’S THEOREM is found in J. W. L. Glaisher, "Note on Cayley’s theorem," Messenger of Mathematics (1878).

Cayley’s theorem, referring to a theorem given by Cayley in 1843, appears in 1897 in Abel’s Theorem and the Allied Theory Including the Theory of the Theta Functions by H. F. Baker (1897).

The term Cayley’s theorem (every group is isomorphic to some permutation group) was apparently introduced in 1916 by G. A. Miller. He wrote Part I of the book Theory and Applications of Finite Groups by Miller, Blichfeldt and Dickson. He liked the idea of listing the most important theorems, with names, so when this theorem had no name he introduced one. His footnote on p. 64 says:

This theorem is fundamental, as it reduces the study of abstract groups uniquely to that of regular substitution groups. The rectangular array by means of which it was proved is often called Cayley’s Table, and it was used by Cayley in his first article on group theory, Philosophical Magazine, vol. 7 (1854), p. 49. The theorem may be called Cayley’s Theorem, and it might reasonably be regarded as third in order of importance, being preceded only by the theorems of Lagrange and Sylow.

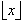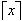The terms CEILING FUNCTION and FLOOR FUNCTION appear in Kenneth E. Iverson’s A Programming Language (1962, p. 12): "Two functions are defined: 1. the floor of x (or integral part of x) denoted by and defined as the largest integer not exceeding x, 2. the ceiling of x denoted by and defined as the smallest integer not exceeded by x." This was the first appearance of the terms and symbols, according to R. L. Graham, D. E. Knuth & O. Patashnik Concrete Mathematics: A Foundation for Computer Science (1989, p. 67). Other terms are least integer function and greatest integer function. For notation see Earliest Use of Function Symbols.

CENSORING and TRUNCATION. Anders Hald began his "Maximum Likelihood Estimation of the Parameters of a Normal Distribution which is Truncated at a Known Point," Skandinavisk Actuarietidskrift, 32, (1949), 119-134 by noting that the term truncation had been applied to two cases: one in which "all record is omitted of observations below a given value" and the other in which "the frequency of observations below a given value is recorded but the individual values ... are not specified." To distinguish them, "the distributions will be called truncated and censored respectively."  Hald says that the term "censored" was suggested by J. E. Kerrich.

Hald’s reference for truncation was R. A. Fisher The Sampling Error of Estimated Deviates, Together with Other Illustrations of the Properties and Applications of the Integrals and Derivatives of the Normal Error Function. Mathematical Tables, 1: (1931) xxvi-xxxv, (p. xxxi) and for censoring, W. L. Stevens The Truncated Normal Distribution, Annals of Applied Biology, 24, (1937), 852.

"Truncated," in Hald’s sense of the word, was perhaps first used by K. Pearson & A. Lee "Generalized Probable Error in Multiple Normal Correlation," Biometrika, 6, (1908), 59-68.

[John Aldrich, based on David (2001)]

The CENTER of a circle is defined in Euclid Book 1 definition 16. The word derives from kentron a sharp point. (OED and Schwartzman).

The OED’s earliest quotation comes from Chaucer’s translation (c. 1374) of Boethius De consolatione philosophiæ, “þe sterres of arctour ytourned neye to þe souereyne centre or point.” The OED’s quotation from Billingsley’s translation of Euclid (1570) is “The centre of a Sphere is that poynt which is also the centre of the semicircle.”

CENTRAL ANGLE is found with a use in astronomy in English in 1761 in The Gentlemen’s and Ladies’s Palladium for the Year of our Lord, 1761, where the term is used in reference to an eclipse of the sun. [Google print search, James A. Landau]

Central angle is found in 1811 in Elements of Geometry, 2nd ed., by John Leslie, which has the phrase “The central angle AOB.” [Google print search, James A. Landau]

CENTRAL LIMIT THEOREM. Central limit theorem is in the title of George Pólya’s "Über den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung und das Momentenproblem," Mathematische Zeitschrift, 8 (1920), 171-181 [James A. Landau]. Pólya apparently coined the term in this paper. "Zentral" signified of central importance. Central limit theorem appears in English in 1937 in Random Variables and Probability Distributions by H. Cramér. (David, 1995).

Pólya’s references went back only a decade or two to Markov and Lyapounov but the study of limiting normal behaviour is much older. In the 1730s De Moivre found the normal approximation to the binomial. Then in the early 19^th century Laplace, Poisson, Cauchy and others worked on normal approximations in connection with the theory of least squares. Laplace’s "On the probability of errors of the mean results of a great number of observations and of the most advantageous mean results" Théorie Analytique des Probabilités livre II, chapitre IV, p. 309 was the most influential treatment from that era. A new era began with Chebyshev (1887) and his students Markov (1912) and Lyapounov. Pólya himself belonged to a third era with von Mises (Mathematische Zeitschrift, 4,(1919), 1-97.) Lindeberg (Mathematische Zeitschrift, 15, (1922), 211-225), Feller (Mathematische Zeitschrift, 40, (1935), 521-559, 42, (1937), 301-312.) and others.

(Based on Hald 1998, chapter 17 and L. Le Cam "The Central Limit Theorem Around 1935," Statistical Science, 1, (1986), 78-91.)

See also ERROR, NORMAL and GAUSSIAN.

The term CENTRAL TENDENCY appears to have originated in Psychology and from there passed into the general statistical literature. The term was used by the American psychologist Edward L. Thorndike writing in 1905 in Measurements of Twins. In his “On the Function of Visual Images,” Journal of Philosophy, Psychology and Scientific Methods, 4, (1907), p. 327 Thorndike writes, “Since the average is 95 and the median is 103, the most probably true central tendency is 99.” The phrase “measure of central tendency” appears in Earle Clark “The Horizontal Zero in Frequency Diagrams,” Publications of the American Statistical Association, 15, p. 663: “the mean, median, or other measure of central tendency.” JSTOR Search. Measures of central tendency became one of the main topics of DESCRIPTIVE STATISTICS.

See also LOCATION AND SCALE and the entries for individual measures, AVERAGE, MEAN, MEDIAN, MODE, etc.

CENTROID is found in 1844 in Mathematician 1/105: “The following locus...discloses some elegant properties of the centro•d of a physical or geometrical system.” [OED]

The term CEPSTRUM was introduced by Bogert, Healey, and Tukey in a 1963 paper, "The Quefrency Analysis of Time Series for Echoes: Cepstrum, Pseudoautocovariance, Cross-Cepstrum, and Saphe Cracking." The word was created by interchanging the letters in the word "spectrum."

CESÀRO MEAN and CESÀRO SUM derive from Ernesto Cesàro’s "Sur la multiplication des séries," Bulletin des Sciences Mathématiques, 14, (1890), 114-120. See Kline (pp. 1112-3).

Cesàro’s  mean appears in T. J. l'A. Bromwich Introduction to the Theory of Infinite Series (1908). A JSTOR search found Cesàro summability in W. H. Young "On the Order of Magnitude of the Coefficients of a Fourier Series" Proceedings of the Royal Society, A, 93, (1917), 42-55.

CEVIAN was proposed in French as cévienne in 1888 by Professor A. Poulain (Faculté catholique d'Angers, France). The word honors the Italian mathematician Giovanni Ceva (1647?-1734) [Julio González Cabillón].

An early use of the word in English is by Nathan Altshiller Court in the title "On the Cevians of a Triangle" in Mathematics Magazine 18 (1943) 3-6.

CHAIN. In his ahead-of-time Was sind und Was sollen die Zahlen? (1887), Richard Dedekind introduced the term chain (kette) with two related senses. Improving on his notation and style somewhat, let us take a function f : S ® S. According to him (§37), a "system" (his name for "set") K Ì S is a chain (under f) when f (K ) Ì K.  (Incidentally, from such a "chain" one really gets a descending chain -in one of the more modern uses of this word -, namely, ...Ì f ³(K) Ì f ²(K) Ì f ¹(K) Ì K.) Soon after (§44), he fixes A Ì S and defines the "chain of the system A" (under f ) as the intersection of all chains (under f ) K Ì S such that A Ì K. This formulation sounds familiar today, but in Dedekind’s time it was a breakthrough! Now, it is easy to see (and he did it in §131) that the "chain of A" (under f ) is simply the union of iterated images A È f ¹(A) È f ²(A) È f ³(A) È ..., a result which would yield a simpler definition. But what are the numbers 1, 2, 3, ...? This was precisely the question he intended to answer once and for all through his concept of chain! Gottlob Frege (in his Begriffsschrift, 1879) had similar ideas but his notation was strange and his terminology repulsively philosophic.

Dedekind’s "theory of chains" would come to be quoted or used in many places: in proofs of the "Cantor-Bernstein" theorem (Dedekind-Peano-Zermelo-Whittaker), in Keyser’s "axiom of infinity" (Bull. A. M. S., 1903, p. 424-433), in Zermelo’s second proof of the well-ordering theorem (through his "q -chains", 1908) and in Skolem’s first proof of Löwenheim theorem (1920) - to name only a few. All that said, it is simply wrong to say that "Dedekind’s approach was so complicated that it was not accorded much attention." (Kline, Mathematical Thought from Ancient to Modern Times, p. 988.) Quite the contrary: the term "chain" in that sense did not survive, but the concept paved the way for the more general notion of closure (hull, span) of a set under an entire structure. [This article contributed by Carlos César de Araújo.]

CHAIN RULE. As there are many possible chains and possible rules the expression chain rule has been used in a variety of ways. In commercial arithmetic it has referred to a rule for calculating an equivalence in different units of measure when an intermediate unit of measure is involved. Smith vol. 2 (p. 573) identifies it in early Dutch books, as Den Kettingh-Regel and Den Ketting Reegel. The English phrase is found in 1795 in the title of a book, An entire new System of Mercantile Calculation, by the Use of universal Arbiter Numbers. Introduced by an elementary Description of, and commercial and political Reflections on, universal Trade. Illustrated and exemplified by the Elements of the Chain Rule of Three, the Nature of the Exchanges, and of all Charges and Contingencies on Goods. Which are also reduced to a plain and concise System intirely new and universal. By an old Merchant. [Google print search, James A. Landau]

In another context there is the chain rule of N. Chater and W. H. Chater, “A chain rule for use with determinants and permutations,” Mathematical Gazette, 31, (1947), 279-287.

Today, the chain rule is most likely to refer to one of the oldest and most basic rules in differential calculus. Kline (p. 376) describes a manuscript of Leibniz from 1676 in which the rule is used. However the term chain rule is much more recent and appears to have originated in German in the early twentieth century.

Peter Flor has found Kettenregel in Höhere Mathematik (1921) by Hermann Rothe, where it is used in a slightly different way from modern practice, viz. only for composites of three or more functions. Flor writes, “Here the word 'chain' ('Kette', in German) is suggestive. I tried, rather perfunctorily, to pursue the term further back in time, without success. It seems that around 1910, most authors of textbooks as yet saw no problem in computing dz/dx = (dz/dy)*(dy/dx). On the other hand, when I was a student in Vienna and Hamburg (1953 and later), the word Kettenregel was a well-established part of elementary mathematical terminology, in German, for the rule on differentiating a composite of two functions. I guess that its use must have become general around 1930.”

One of the German works using the term Kettenregel for differentiating a composite of two functions was Richard Courant’s Vorlesungen über differential- und integralrechnung (1927). The section on “Die Differentation der zusammengesetzten Funktionen” (p. 122) contains a treatment of “die Kettenregel.” In 1934 the book was translated into English by E. J. McShane as Differential and Integral Calculus and Kettenregel became the chain rule for differentiating a compound function. The book was widely circulated and James A. Landau suggests that it was this translation that established the German expression with English readers.

Older English texts used variants of the expression, “rule for differentiating a function of a function.” The expression is found in E. B. Wilson’s Advanced Calculus (1912, p. 2) while I. Todhunter’s A treatise on the differential calculus with numerous examples (8^th edition 1878, pp. 37-8) has a “rule” for “the differential coefficient of a function of a function.” In his A course of pure mathematics (1908, p. 216) G. H. Hardy used the expression “composite function” as well as “function of a function.” He was following the French “fonction composée.” The term “composite function” has become standard and we usually write of “the chain rule for differentiating a composite function.”

CHAMBER. See the entry APARTMENT, BUILDING and CHAMBER.

CHANCE and the DOCTRINE OF CHANCES. See PROBABILITY.

CHAOS appears in 1938 in Norbert Wiener, "The homogeneous chaos," Am. J. Math. 60, 897-936. In the note on this paper in Norbert Wiener Collected Works Volume 1 (p. 612) L. Gross writes that, "By a chaos Wiener meant an additive function defined on a ring of subsets of a given set whose values are random variables on a probability space."

Chaos in its more common meaning today was coined by  James A. Yorke and Tien Yien Li in their classic paper "Period Three Implies Chaos" [American Mathematical Monthly, vol. 82, no. 10, pp. 985-992, 1975], in which they describe the behavior of some particular flows as chaotic [Julio González Cabillón].

It should be stressed that some mathematicians do not feel comfortable with the term "chaos". As an example we quote Paul Halmos in his Has Progress in Mathematics Slowed Down? (Am. Math. Monthly, 1990, p. 563):

Why the word "chaos" is used? The reason seems to be (...) a subjective (not really a mathematical) reaction to an unexpected appearance of discontinuity. A possible source of confusion is that the startling discontinuity can occur at two different parts of the theory. Frequently a dynamical system depends on some parameters (...), and, of course, (...) on the initial point. The startling change of the Hénon family (from periodic to strange attractor) is regarded as chaos - unpredictability - and the very existence of the Hénon strange attractor, not obviously visible in the definition of the dynamical system, is regarded as chaos - unpredictability. I would like to register a protest vote against the attitude that the terminology implies. The results of nontrivial mathematics are often startling, and when infinity is involved they are even more likely to be so. It’s not easy to tell by looking at a transformation what its infinite iterates will do - but just because different inputs sometimes produce discontinuously outputs doesn't justify describing them as chaotic.

The CHAPMAN-KOLMOGOROV EQUATIONS for Markov processes refer to Sydney Chapman “On the Brownian Displacements and Thermal Diffusion of Grains Suspended in a Non-Uniform Fluid,” Proceedings of the Royal Society of London, Series A, 119, (1928), 34-54 and A. N. Kolmogorov “Über die analytischen Methoden in der Wahrscheinlichkeitsrechnung,” Math. Ann. 104, (1931), 415-458. E. B. Dynkin points out that Kolmogorov himself referred to the physicist Smoluchovski who had considered a special situation. (Kolmogorov and the Theory of Markov Processes, Annals of Probability, 17, (1989), p. 823.) D. G. Kendall writes in his obituary of Kolmogorov, “I once asked Sydney Chapman about ‘Chapman-Kolmogorov’, and was surprised to find that he did not know of that terminology.” (Bulletin of the London Mathematical Society, 22, (1990) p. 35.) A JSTOR search found the term “Chapman-Kolmogoroff equation” in Willy Feller “On the Integro-Differential Equations of Purely Discontinuous Markoff Processes,” Transactions of the American Mathematical Society, 48, (1940), 488-515.

This entry was contributed by John Aldrich. See also MARKOV PROCESS.

CHARACTER (group character) appears in title of the paper "Uber die Gruppencharactere" by Ferdinand Georg Frobenius (1849-1917), which was presented to the Berlin Academy on July 16, 1896.

According to Shapiro:

However, in Dedekind’s edition of Dirichlet’s Vorlesungen ueber Zahlentheorie in 1894, Dedekind included a footnote in which he singled out the notion of "character," defined it explicitly, and denoted it by chi(n). [6.55]. However, he did not give the function a name. Weber’s Lehrbuch der Algebra, II, 1899, defined the function chi(A) as a "Gruppencharakter," and developed some of its elementary properties. . . E. Landau’s use of the symbol chi(n) in his texts, together with the terms "charakter and Hauptcharakter" most probably led to the subsequent widespread acceptance of the notation and terminology. Landau credited G. Torelli, 1901, with playing a major role in applying the theory of functions to the study of prime numbers [6.56]. Landau’s treatment of characters [6.5.7] suggests that it was Torelli’s use of notation that led to Landau’s. This is further supported by a 1918 paper of Landau [6.58], where chi(n) is introduced in connection with a discussion of Torelli’s results.

The term CHARACTERISTIC (as used in logarithms) was introduced by Henry Briggs (1561-1631), who used the term in 1624 in Arithmetica logarithmica (Cajori 1919, page 152; Boyer, page 345).

According to Smith (vol. 2, page 514), the term characteristic "was suggested by Briggs (1624) and is used in the 1628 edition of Vlacq." In a footnote, he provides the citation from Vlacq: "...prima nota versus sinistram, quam Characteristicam appellare poterimus..."

Scott (page 136) provides the following citation from Vlacq’s Tabulae Sinuum, Tangentium et Secantium: "Here you will note that the first figure of the logarithm, which is called the characteristic is always less by unity than the nuber of figures in the number whose logarithm is taken" (p. xvii).

Scott (page 137) also provides this citation from Adriani Vlacq, Tabulae Sinuum, Tangentium et Secantium, et Logarithmorum. Sinuum, Tangentium et Numerorum ab Unitate ad 100000: "Si datur numerus 3.567894 = 3 567894/1000000 vel 35 67894/100000 vel 356 7894/10000 Logarithmi eorum iidem sunt, qui numeri integri 3567894, escepta tantum Characteristica aut prima figura, et modus eos inveniendi prorsus est idem." [Scott shows the decimal points as raised dots.]

The term index was another early term for the characteristic of a logarithm.

CHARACTERISTIC DETERMINANT, EQUATION, POLYNOMIAL, ROOT, VALUE, VECTOR. See EIGENVALUE.

CHARACTERISTIC FUNCTION (1) of a random variable. The first person to apply characteristic functions was Laplace in 1810, though he already had a simple form in 1785. Cauchy was probably the first to apply a name to the functions, using the term fonction auxiliaire. In 1919 Richard von Mises used the term komplexe Adjunkte in his "Grundlagen der Wahrscheinlichkeitsrechnung," Math. Zeit. 5, (1919) 52-99. See Hald (1998, chapter 17).

The term characteristic function was first used by Jules Henri Poincaré (1854-1912) in Calcul des probabilités (p. 206) in 1912. He wrote "fonction caractéristique." Poincaré’s usage corresponds with what is today called the moment generating function. This information is taken from H. A. David, "First (?) Occurrence of Common Terms in Mathematical Statistics," The American Statistician, May 1995, vol 49, no 2 121-133.

In 1922 P. Lévy used the term characteristic function in the title "Sur la determination des lois de probabilité par leurs fonctions charactéristiques," Comptes Rendus, 172, (1922), 854-856.

Characteristic function appears in English in 1934 in S. Kullback, "An Application of Characteristic Functions to the Distribution Problem of Statistics," Annals of Mathematical Statistics, 5, 263-307 (David, 1995).

See GENERATING FUNCTION and MOMENT GENERATING FUNCTION.

CHARACTERISTIC FUNCTION (2) of a set A with respect to a “superset” U is widely used to designate the function from U to {0, 1} that is 1 on A and 0 on its complement. The name explains the common choice of the Greek letter χ (chi, which represents kh or ch) for this function. With this meaning, the term “la fonction caractéristique” was introduced by C. de la Vallé Poussin (1866-1962) in “Sur L'Integrale de Lebesgue,” Transactions of the American Mathematical Society, 16, (1915), p. 440.

Probably to avoid confusion with the other meaning (especially in probability theory, where both notions are useful), some prefer to use the term "indicator function". Besides, it is interesting no note that many logicians turn the usual order of things upside-down: for them, "characteristic function" of a set A (of natural numbers, 0 included) refers to the characteristic function of the complement! In his Foundations of mathematics (1968), W. S. Hatcher explains (p. 215):

In analysis, the characteristic function is usually 1 on the set and 0 off the set, but we generally reverse the procedure in number theory [[more precisely, in recursion theory]]. The reason stems from the minimalization rule and the fact that, when we treat characteristic functions in this way, a given problem often reduces to finding the zeros of some function. In analysis, we want the characteristic functions to be 1 on the set so that the measure of a set will be the integral of its characteristic function.

See also INDICATOR FUNCTION. [Hans Fischer, Brian Dawkins, Ken Pledger, Carlos César de Araújo]

The term CHARACTERISTIC TRIANGLE was used by Leibniz and apparently coined by him, as triangulum characteristicum.

CHEBYSHEV POLYONOMIALS. These were introduced by P. L. Chebyshev in his "Sur l'interpolation dans le cas d'un grand nombre de donnees fournies par les observations," (Russian original 1855, published in French in Liouville’s J. Math. Pures App. 3, (1858), 289-323. (Reprinted in Oeuvres I, p. 387)

CHEBYSHEV’S INEQUALITY. The inequality appeared in L. J. Bienaymé Considérations à l'appui de la découverte de Laplace ... Comptes Rendus de l'Académie des Sciences, 37, (1853), 309-324. The paper was reprinted in Crelle’s Journal in 1867 where it preceded a paper translated from the Russian where the inequality is re-derived and used to prove the weak law of large numbers: P. L Chebyshev’s "Des Valeurs Moyennes." See also Oeuvres p. 687. In the later literature Bienaymé’s contribution was often overlooked, thus A. A. Markov refers to "die Ungleichheit von Tschebyscheff." in Wahrscheinlichkeitsrechnung (1912, p. 56).

(Based on C. C. Heyde & E. Seneta I. J. Bienaymé: Statistical Theory Anticipated, 1977)

CHECKSUM is found in 1940 in Punched Card Methods in Scientific Computation by Wallace J. Eckert: "Check sums detect misplaced cards and errors of transposition" [OED2].

CHERNOFF BOUND. The bound appears in Herman Chernoff’s “A Measure of Asymptotic Efficiency for Tests of a Hypothesis Based on the sum of Observations,” Annals of Mathematical Statistics, 23, No. 4. (Dec., 1952), pp. 493-507.

Chernoff, however, credited the result to Herman Rubin, as he explained in a conversation in Statistical Science, 11, No. 4. (Nov., 1996), p. 340. Project Euclid

Rubin claimed that part of my derivation, giving the lower bounds, could be obtained much more easily. After working so hard, I doubted it very much. He showed me the Chebyshev type of proof that gives rise to what’s now called the Chernoff bound, but it is certainly Rubin’s. When I wrote up the technical report, I mentioned his assistance but when I submitted the paper for publication, I left it out because it was so trivial and it never occurred to me that this would be one of the things that would lead to my fame in electrical engineering circles. That inequality turned out to be a very important result as far as information theory is concerned, and so the lower bound has been called the Chernoff bound ever since. I am very unhappy about the fact that I did not properly credit Rubin at that time because I thought it was a rather trivial lemma, but many things are only trivial once you know them.

CHILIAD is found in English in 1598 in Greene in conceipt new raised from his grave by John Dickenson: "With a chiliade of crosse Fortunes" [OED2].

In 1617 Brigs published Logarithmorum Chilias prima (Logarithms of Numbers from 1 to 1,000).

The term CHINESE REMAINDER THEOREM is found in 1929 in Introduction to the theory of numbers by Leonard Eugene Dickson [James A. Landau].

CHI SQUARE. Karl Pearson introduced the chi-square test and the name for it in “On the Criterion that a Given System of Deviations from the Probable in the Case of a Correlated System of Variables is such that it can be Reasonably Supposed to have Arisen from Random Sampling,” Philosophical Magazine, 50, (1900), 157-175. Pearson had been in the habit of writing the exponent in the multivariate normal density as -½χ²; see e.g. equation (iii) on p. 263 of “Mathematical Contributions to the Theory of Evolution. III. Regression, Heredity and Panmixia” (1896). The idea of a chi-square distribution as one of a family of distributions related to the normal was R. A. Fisher’s: see his On a Distribution Yielding the Error Functions of Several Well Known Statistics (1924). The English statisticians were not aware that the German geodesist F. R. Helmert had effectively obtained the distribution in 1876 in his work on the distribution of the sample variance. See the entry HELMERT TRANSFORMATION for the details. [James A. Landau, John Aldrich].

See DEGREES OF FREEDOM, GOODNESS OF FIT, STUDENT’S t-DISTRIBUTION.

The names CHOLESKY algorithm, decomposition, factorisation, etc. commemorate the work of the French geodesist André-Louis Cholesky. Commandant Cholesky (b. 1875) was killed in action on August 31st, 1918 and his method for solving the normal equations of least squares was published by a colleague, Benoit, in 1924 (Bulletin geodesique, 7 (1), 67-77). The method is based on the factorisation of a positive definite matrix A = L L^T where L is lower triangular with positive diagonal entries. Although the factorisation is now associated with Cholesky, it was known to Gauss and even to Lagrange who used it in his work on the second-order conditions in multivariate calculus. Gauss, incidentally, not only devised least squares methods for reducing geodetic observations but did field work as a surveyor. The use of matrices for writing least squares algorithms became established in the 1940s. An important contributor was Paul S. Dwyer with his "A Matrix Presentation of Least Squares and Correlation Theory with Matrix Justification of Improved Methods of Solution," Annals of Mathematical Statistics, 15, (1944), 82-89. Dwyer proposed a square root method and was surprised that it had not been proposed before. It was Cholesky’s method and his name began to be associated with it in the English statistics and numerical analysis literature from the early 1950s and with the underlying matrix result some time later.

(The eulogy Benoit composed for Cholesky appears in an NA Digest post. This entry was contributed by John Aldrich.)

CHORD is found in English in 1551 in The Pathwaie to Knowledge by Robert Recorde:

Defin., If the line goe crosse the circle, and passe beside the centre, then is it called a corde, or a stryngline.

A JSTOR search finds the phrase Church’s thesis in December 1945 in S. C. Kleene, "On the Interpretation of Intuitionistic Number Theory," The Journal of Symbolic Logic, Vol. 10, No. 4, pp. 109-124.

CIPHER. See ZERO.

CIRCLE. According to Todhunter’s translation of Euclid, Book 1 Def. 15 says "a circle is a plane figure bounded by one line, which is called the circumference ..." However Proposition 1 assumes circles consist of their circumferences: "From the point C, at which the circles cut one another, draw the straight lines ..." Heath’s translation has the same problems: Def 15 "A circle is a plane figure contained by one line such that...", Prop 1 "... and from the point C, in which the circles cut one another, to the points A, B let the straight lines..." [John Harper].

A Mathematical and Philosophical Dictionary (1796) has, "The circumference or periphery itself is called the circle, though improperly, as that name denotes the space contained within the circumference."

Modern geometry texts define a circle as the set of points in a plane equidistant from a given point; the term disk is used for the circle and its interior.

CIRCLE GRAPH is found in 1919 in School Statistics and Publicity by Carter Alexander: "The data shown in this circle graph for Rockford may be presented in a bar graph which permits of placing the figures so they can be added." [Google print search]

CIRCLE OF CONVERGENCE appears in the Century Dictionary (1889-1897).

Circle of convergence appears in 1893 in A Treatise on the Theory of Functions by James Harkness and Frank Morley in the heading "The circle of convergence."

Circle of convergence also appears in 1898 in Introduction to the theory of analytic functions by Harkness and Morley: "Hence there is a frontier value R such that when |x| > R there is divergence. That is, with the circle (R) the series is absolutely convergent and without the circle it is divergent. The circle (R) is called the circle of convergence.

The term CIRCULAR COORDINATES was used by Cayley. Later writers used the term "minimal coordinates" (DSB).

CIRCULAR FUNCTION. Lacroix used fonctions circulaires in Traité élémentaire de calcul différentiel et de calcul intégral (1797-1800).

Circular function appears in 1831 in the second edition of Elements of the Differential Calculus (1836) by John Radford Young: "Thus, a^x, a log x, sin x, &c., are transcendental functions: the first is an exponential function, the second a logarithmic function, and the third a circular function" [James A. Landau]

CIRCUMCENTER, CIRCUMCIRCLE, EXCENTER, EXCIRCLE, INCENTER, INCIRCLE, MIDCIRCLE were proposed in 1883 by William Henry Hoar Hudson in letters to Nature published in May 1883. A letter published on May 7, 1883, has: “I beg leave to suggest the following names: circumcircle, incircle, excircle, and midcircle ... ”

On May 31, 1883, another letter from Hudson has: “Continuing my suggestion in your number of May 3 (p. 7), I propose not only to call the circle circumscribing a triangle the circumcircle, but also to call its centre the circumcentre, and in the same way to speak of the incentre, the three excentres (namely, the a-excentre, the b-excentre, and the c-excentre), and the midcentre. The line joining the circumcentre to the orthocentre, on which the masscentre and the midcentre lie, may be appropriately called the central line of the triangle. Similar abbreviations would apply to the radii of these circles; they might be spoken of as the circumradius, the inradius, the a-exradius, the b-exradius, the c extradius, and the midradius.”

[James A. Landau]

CIRCUMFERENCE. Periphereia was used by Heraclitus: "The beginning and end join on the circumference of the circle (kuklou periphereias)" (D. V. 12 B 103) (Michael Fried).

Periphereia was also used by Euclid.

Circumferentia is a Latin translation of the earlier Greek term periphereia.

A Google print search finds circumference in a facsimile of what seems to be a 1586 English translation of L’Académie françoise from 1577. However, the title page is not included in this facsimile: “nature hath limited certaine bounds of wealth, which are traced out vpon a certaine Center, and vpon the circumference of their necessitie.”

A Google print search also finds circumference in The Arte of English Poesie, the title page of which seems to say that this is an 1869 reprint of a 1589 book: “The circle is his largest compasse or circumference: the center is his middle and indiuisible point: the beame is a line stretching directly from the circle to the center, and contrariwise from the center to the circle. By this description our maker may fashion his meetre in Roundel, either with the circumference, and that is circlewise, or from the circumference, that is, like a beame, or by the circumference, and that is ouerthwart and dyametrally from one side of the circle to the other.” [James A. Landau]

Circumference is found in modern translations of the Bible, in 2 Chronicles 4:2, Jeremiah 52:21, and Ezekiel 48:35. However, the word does not appear in the King James version.

CIRCUMSCRIBE is found in English in 1570 in Billingsley’s translation of Euclid: "How a triangle ... may be circumscribed about a circle" [OED].

Circumscribed polygon is found in 1714 in Theorems Selected out of Archimedes by Andrew Tacquet: “But Polygons circumscrib’d infinitely about the Circle end in the Circle, (by the 3d of this Book); and in like manner Triangles (as I will shew by and by) which have for their Base the Circuit of the circumscribed Polygon.” [Google print search, James A. Landau]

CISSOID. This term is mentioned by Geminus (c. 130 BC - c. 70 BC), according to Proclus, although the original work of Geminus does not survive.

Cissoid appears in Proclus (in Euclid, p.111, 152, 177...). It is not completely clear what curve Proclus was calling the cissoid (see W. Knorr, The Ancient Tradition in Geometric Problems, New York: Dover Publications, Inc., pp.246ff for a detailed discussion).

Mathematics Dictionary (1949) by James says "the cissoid was first studied by Diocles about 200 B. C., who gave it the name 'Cissoid' (meaning ivy)"; however, according to Michael Fried, Diocles himself does not call his curve a cissoid.

In the 17th century, cissoid became associated with a curve described by Diocles in his work, On Burning Mirrors.

Cissoid is found in English in 1656 in a translation of Elements of philosophy the first section... by T. Hobbes: “When they cannot exhibit the quantity sought for with the helpe of a conique Section, they call it a Lineary Probleme... Of this kinde are the Spiral lines, the Quadratices, the Concheoides, and the Cissoeides.” [OED]

CLAIRAUT EQUATION is the name given to a differential equation studied by Alexis Clairaut in his “Solution de plusieurs Problemes où il s'agit de trouver des Courbes dont la propriété consiste dans une certaine relation entre leurs branches, exprimée par une Équation donnée,” Histoire Acad. R. Sci. Paris (1734) (1736) pp. 196–215. See Klein (ch. 21 “Ordinary Differential Equations in the Eighteenth Century”) and the entry in the Enyclopedia of Mathematics.

In English, Clairault’s theorem is found in 1810 in Encyclopaedia Londinensis; or, Universal Dictionary of Arts, Sciences, and Literature, Volume II: “The fifth column shews the value of 2 corresponding to every value of P—11, according to Clairault’s theorem.” [“P—11” and “2” are column headings in the immediately following table. Google print search, James A. Landau]

CLAIRAUT’S THEOREM, SCHWARZ’ THEOREM and YOUNG’S THEOREM on the equality of mixed partial derivatives. The history of this topic, spanning two centuries, is recounted by T. J. Higgins “A Note on the History of Mixed Partial Derivatives,” Scripta Mathematica, 7, (1940), 59-62; reproduced here. Other mathematicians were involved but Alexis Clairaut was the first to try to establish the equality of the second mixed partials in his “Sur l'integration ou la construction des equations différentielles du premier ordre,” Memoires de l'Académie Royale des Sciences, 2, (1740), 420-421. H. A. Schwarz produced the first acceptable proof in his “Communication,” Archives des Sciences Physiques et Naturelles, 48, (1873), 38-44 and W. H. Young provided a weaker set of conditions in his “On the Conditions for the Reversibility of the Order of Partial Differentiation,” Proceedings of the Royal Society of Edinburgh, 29, (1908-09), 136-164. It is not unusual for the names of several people to be attached to the same theorem; see the entry on EPONYMY. [John Aldrich]

The term CLASS (of a curve) is due to Joseph-Diez Gergonne (1771-1859). He used "curve of class m" for the polar reciprocal of a curve of order m in Annales 18 (1827-30) (Smith vol. I and DSB).

CLASS (in set theory). In the early English literature the word class was used where set would be used today, e.g. in Bertrand Russell’s Principles of Mathematics (1903). Russell was following Peano. Classe appears in his “Dizionario di Matematica,” Revue de mathématiques, 7, (1900-1), 160-172 and is described as "idea primitiva." In the von Neumann set theory classes and sets are distinguished, so that every set is a class, but not conversely. The von Neumann publications begin with "Eine Axiomatisiereung der Mengenlehre" (1925) (translated in van Heijenoort (1967)) with later work in English by Bernays and Gödel. Bernays writes: "According to the leading idea of the von Neumann set theory we have to deal with two kinds of individuals, which we may distinguish as sets and classes." from "A System of Axiomatic Set Theory," 2, (1937) p. 66. [John Aldrich]

See SET.

CLASS FIELD. The modern concept of a class field is due to Teiji Takagi.

Leopold Kronecker (1823-1891) used the terminology "species associated with a field k."

Class field was introduced by Heinrich Weber (1842-1913) in Elliptische Funktionen und algebraische Zahlen in 1891. He originally only used the term for the Kronecker class field, but in 1896 enlarged the concept of a class field to fields K associated with a congruence class group in k, but only in the second edition of his Lehrbuch der Algebra was the term class field used to designate a general class field. (Günther Frei in "Heinrich Weber and the Emergence of Class Field Theory")

The terms CLASSICAL GROUP and CLASSICAL INVARIANT THEORY were coined by Hermann Weyl (1885-1955) and appear in The classical groups, their invariants and representations (1939).

CLASSICAL PROBABILITY. This term for probability as defined by Laplace and earlier writers including De Moivre came into use in the 1930s when alternative definitions were widely canvassed. J. V. Uspensky (Introduction to Mathematical Probability, 1937, p. 8) gave the "classical definition," which he favored, and criticized the "new definitions" (von Mises) and "the attempt to build up the theory of probability as an axiomatic science" (Kolmogorov) [John Aldrich].

See PROBABILITY.

CLASSICAL statistical inference. The polar pair "classical" and "Bayesian" have figured in discussions of the foundations of statistical inference since the 1960s. The body of work to which "classical" was attached went back only to the 1920s and -30s but, as Schlaifer wrote in 1959 (Probability and Statistics for Business Decisions, p. 607), "it is expounded in virtually every course on statistics [in the United States] and is adhered to by the great majority of practicing statisticians." Schlaifer and a few others were sponsoring a rejuvenated Bayesian alternative. The "classical" tag may have derived some authority from Neyman’s "Outline of a Theory of Statistical Estimation based on the Classical Theory of Probability" (Philosophical Transactions of the Royal Society, 236, (1937), 333-380), one of the classics of classical statistics. The non-classical possibility Neyman had in mind and rejected was the Bayesian theory of Jeffreys. Confusingly Neyman’s "classical theory of probability" has more to do with Kolmogorov and von Mises than with Laplace [John Aldrich].

See BAYES.

CLELIA was coined by Guido Grandi (1671-1742). He named the curve after Countess Clelia Borromeo (DSB).

CLOSED (elements produced by an operation are in the set). Closed cycle appears in Eliakim Hastings Moore, "A Definition of Abstract Groups," Transactions of the American Mathematical Society, Vol. 3, No. 4. (Oct., 1902): "For in any finite set of elements with multiplication-table satisfying (1, 2) there exists a closed cycle of (one or more) elements, each of which is the square of the preceding element in the cycle...."

The phrase "closed under multiplication" appears in Saul Epsteen, J. H. Maclagan-Wedderburn, "On the Structure of Hypercomplex Number Systems," Transactions of the American Mathematical Society, Vol. 6, No. 2. (Apr., 1905).

CLOSED CURVE. In 1551 in Pathway to Knowledge Robert Recorde wrote, "Defin., Lynes make diuerse figures also, though properly thei maie not be called figures, as I said before (vnles the lines do close)" [OED].

Closed curve is found in 1855 in An elementary treatise on mechanics, embracing the theory of statics and dynamics, and its application to solids and fluids by Augustus W. Smith: "Since the above principle is true, whatever be the number of sides of the polygon, it is true when the number becomes indefinitely great, or when the base becomes a continued closed curve, as a circle, an ellipse, &c.; or, the center of gravity of a cone, right or oblique, and on any base, is one fourth the distance from the center of gravity of the base to the vertex" [University of Michigan Digital Library].

CLOSED SET. Georg Cantor (1845-1918) in "De la puissance des ensembles parfaits de points," Acta Mathematica IV, March 4, 1884, introduced (in French) the concept and the term "ensemble fermé [Udai Venedem].

Closed is found in English in 1902 in Proc. Lond. Math. Soc. XXXIV: "Every example of such a set [of points] is theoretically obtainable in this way. For..it cannot be closed, as it would then be perfect and nowhere dense" [OED].

CLUSTER ANALYSIS is found in 1939 in Cluster Analysis by R. C. Tryon [James A. Landau].

CLUSTER SAMPLING. A JSTOR search found this term in use in Morris H. Hansen and William N. Hurwitz “Relative Efficiencies of Various Sampling Units in Population Inquiries,” Journal of the American Statistical Association, 37, (1942), 89-94.

COCHLEOID (or COCHLIOID). In 1685 John Wallis referred to this curve as the cochlea:

... the Cochlea, or Spiral about a Cylinder, arising from a Circular motion about an Ax, together with a Rectilinear (in the Surface of the Cylinder) Perpendicular to the Plain of such Circle, (or, if the Cylinder be Scalene at such Angles with the Plain of the Circle, as is the Axis of that Cylinder) both motions being uniform, but not in the same Plain.

Er hat sie daher die Cochleoïde genannt, von *cochlea* = Schneckenhaus. [Therefore, it was christened the Cochleoid, from *cochlea* = snail’s house.]

COCHRAN’S THEOREM on quadratic forms in normal variables. William G. Cochran published the theorem in his “The Distribution of Quadratic Forms in a Normal System, with Applications to the Analysis of Covariance,” Proceedings of the Cambridge Philosophical Society, 30, (1934), 178-191. The paper is also noteworthy for its use of some concepts of matrix theory; in 1934 the application of matrix theory to mathematical statistics was in its infancy. A JSTOR search found the expression “Cochran’s theorem” in W. G. Madow “Contributions to the Theory of Multivariate Statistical Analysis,” Transactions of the American Mathematical Society, 44, (1938), p. 458.

See the entries COVARIANCE and CHI-SQUARE; see also the remarks on matrix notation in Earliest Uses of Symbols in Probability and Statistics.

COEFFICIENT. Cajori (1919, page 139) writes, "Vieta used the term 'coefficient' but it was little used before the close of the seventeenth century." Cajori provides a footnote reference: Encyclopédie des sciences mathématiques, Tome I, Vol. 2, 1907, p. 2. According to Smith (vol. 2, page 393), Vieta coined the term.

The term COEFFICIENT OF VARIATION appears in 1896 in Karl Pearson, "Mathematical Contributions to the Theory of Evolution.  III. Regression, Heredity and Panmixia," Philosophical Transactions of the Royal Society of London, Ser. A. 187, 253-318: "we may take as a measure of variation the ratio of standard deviation to mean, or what is more convenient, this quantity multiplied by 100. We shall, accordingly, define ...the coefficient of variation ..." (p. 277) (David, 1995). The term is due to Pearson (Cajori 1919, page 382). According to the DSB, he introduced the term in this paper.

CO-FACTOR is found in 1849 in Trigonometry and Double Algebra by Augustus De Morgan: "When an expression consists of terms, let them be called co-terms; when of factors, co-factors [University of Michigan Historic Math Collection].

COHERENT in subjective probability theory. The term is derived from the "cohérence" of B. de Finetti’s "La prévision: ses lois logiques, ses sources subjectives," Annales de l'Institute Henri Poincaré, 7, (1937) 1-68. The English term is found in the mid 1950s, most conspicuously in Abner Shimony "Coherence and the Axioms of Confirmation," Journal of Symbolic Logic, 20, (1955), 1-28.

The term "consistency" was used in F. P. Ramsey’s treatment of subjective probability, "Truth and Probability" (1926) (published in The Foundations of Mathematics and other Logical Essays (1931)): the calculus of probabilities can be "interpreted as a consistent calculus of partial belief."

(Based on a note to the translation of de Finetti (1937) in H. E. Kyburg Jr. & H. E. Smokler (eds) Studies in Subjective Probability (1964))

COLLECTIVE (Kollektiv) was the basic concept in the probability theory of Richard von Mises (1883-1953). It first appears in his "Grundlagen der Wahrscheinlichkeitsrechnung," Math. Zeit. 5, (1919), 52-99. Some writers in English used Kollektiv, e.g. J. B. S. Haldane (1932) A Note on Inverse Probability, Proceedings of the Cambridge Philosophical Society, 28, 55-61 but collective is used in Probability, Statistics and Truth (1939), the English translation of von Mises’s Wahrscheinlichkeit Statistik und Wahrheit (1928).

The word COMBINANT was coined by James Joseph Sylvester (DSB).

The word appears in a paper by Sylvester in 1853 in Camb. & Dublin Math. Jrnl. VIII. 257: "What I term a combinant" [OED].

COMBINATION was used in its present sense by both Pascal and Wallis, according to Smith (vol. 2, page 528).

In a letter to Fermat dated July 29, 1654, Pascal wrote a sentence which is translated from French:

If from any number of letters, as 8 for example, A, B, C, D, E, F, G, H, you take all the possible combinations of 4 letters and then all possible combinations of 5 letters, and then of 6, and then of 7, of 8, etc., and thus you would take all possible combinations, I say that if you add together half the combinations of 4 with each of the higher combinations, the sum will be the number equal to the number of the quaternary progression beginning with 2 which is half of the entire number.

Combinations is found in English in 1673 in the title Treatise of Algebra...of the Cono-Cuneus, Angular Sections, Angles of Contact, Combinations, Alternations, etc. by John Wallis [OED].

Leibniz used complexiones for the general term, reserving combinationes for groups of three.

Eberhard Knobloch writes in "The Mathematical Studies of G. W. Leibniz on Combinatorics," Historia Mathematica 1 (1974):

Leibniz’s terminology for partitions, just as for symmetric functions, is not consistent. In his Ars Combinatoria he speaks of "discerptiones, Zerfällungen" as mentioned above, and defines them as special cases of "complexiones" (combinations). The Latin term "discerptio" he uses most, and it appears in numerous manuscripts up to his death. When he wants to refer to specific partitions into 1, 2, 3, 4 ... summands, he writes "uniscerptiones, biscerptiones, triscerptiones, quadriscerptiones..." and sometimes also "1scerptiones, 2scerptiones..." evidently following his former usage for combinations of certain sizes in the Ars Combinatoria. I have found only two places where Leibniz applies the general term "discerptio" to the special partition into two summands.

Combinatorial analysis is found in English in 1818 in the title Essays on the Combinatorial Analysis by P. Nicholson [OED].

In the twentieth century Kombinatorik became anglicised as Combinatorics (cf. Statistik to Statistics). An early use of the term combinatorics is by F. W. Levi in an essay entitled "On a method of finite combinatorics which applies to the theory of infinite groups," published in the Bulletin of the Calcutta Mathematical Society, vol. 32, pp. 65-68, 1940 [Julio González Cabillón].

For the symbols used in combinatoriics see SYMBOLS IN COMBINATORIAL ANALYSIS on the Symbols in Probability and Statistics page.

COMMENSURABLE is found in English in 1557 in The Whetstone of Witte by Robert Recorde [OED].

COMMON DIFFERENCE is found in 1658 in Trigonometria Britanica: Or, the Doctrine of Triangles by John Newton: “Seek the Logarithme of the five first figures by the preceeding Probleme, and the logarithme of the common difference in the last columne of the page, and say. As the Logarithme of 10 1.00000. Is to the logarithme difference. So is the logarithme of the last figure in the number propounded, to the logarithme of the part proportionall.” [Google print search, James A. Landau]

COMMON FRACTION. Thomas Digges (1572) spoke of "the vulgare or common Fractions" (Smith vol. 2, page 219).

COMMON LOGARITHM appears in 1742 in Tables of Logarithms For all numbers from 1 to 102100 by William Gardiner: “The common Logarithm of a number is the Index of that power of 10, which is equal to the number.” [Google print search, James A. Landau]

Common system of logarithms appears in the 1828 Webster dictionary, in the definition of radix: "Thus in Briggs', or the common system of logarithms, the radix is 10; in Napier’s, it is 2.7182818284."

COMMON RATIO is found in 1694 in Pleasure with Profit: Consisting of Recreations of Divers Kinds by William Leybourn: “Let the three Numbers be (2, 6, 18.) And let the common Ratio be (3.) The first Term is (2.) The second Term is 2 into 3 (viz. 6.) The third Term is 2 into the Square of 3 (viz. 9.) equal to 18. And from hence it is evident, That the first Term drawn into the third (viz. 2 into 18,) is equal to 2 into 2 (viz. 4,) and that into the Square of 3 the common Ratio (viz. 9).” [Google print search, James A. Landau]

COMMUTATIVE and DISTRIBUTIVE were used (in French) by François Joseph Servois (1768-1847) in a memoir published in Annales de Gergonne (volume V, no. IV, October 1, 1814). He introduced the terms as follows (pp. 98-99):

3. Soit

f(x + y + ...) = fx + fy + ...

Les fonctions qui, comme f, sont telles que la fonction de la somme (algébrique) d'un nombre quelconque de quantites est égale a la somme des fonctions pareilles de chacune de ces quantités, seront appelées distributives.

Ainsi, parce que

a(x + y + ...) = ax + ay + ...; E(x + y + ...) = Ex + Ey + ...; ...

le facteur 'a', l'état varié E, ... sont des fonctions distributives; mais, comme on n'a pas

Sin.(x + y + ...) = Sin.x + Sin.y + ...; L(x + y + ...) = Lx + Ly + ...;

...les sinus, les logarithmes naturels, ... ne sont point des fonctions distributives.

4. Soit

fgz = gfz.

Les fonctions qui, comme f et g, sont telles qu'elles donnent des résultats identiques, quel que soit l'ordre dans lequel on les applique au sujet, seront appelées commutatives entre elles.

Ainsi, parce que qu'on a

abz = baz ; aEz = Eaz ; ...

les facteurs constans 'a', 'b', le facteur constant 'a' et l'état varié E, sont des fonctions commutatives entre elles; mais comme, 'a' etant toujours constant et 'x' variable, on n'a pas

Sin.az = a Sin.z ; Exz = xEz ; Dxz = xDz [D = delta]; ...

il s'ensuit que le sinus avec le facteur constant, l'état varié ou la difference avec le facteur variable, ... n'appartiennent point a la classe des fonctions commutatives entre elles.

(These citations were provided by Julio González Cabillón).

Commutative law is found in English 1841 in Examples of the processes of the differential and integral calculus by D. F. Gregory: “The first of these laws is called the commutative law, and symbols which are subject to it are called commutative symbols.” [Xavier Gracia]

In 1854, Cayley used convertible: "...these symbols are not in general convertible. but are associative."

COMPACT was introduced by Maurice René Fréchet (1878-1973) in 1906, in Rendiconti del Circolo Matematico di Palermo vol. 22 p. 6. He wrote:

Nous dirons qu'un ensemble est compact lorsqu'il ne comprend qu'un nombre fini d'éléments ou lorsque toute infinité de ses éléments donne lieu à au moins un élément limite.

This citation was provided by Mark Dunn.

In his 1906 thesis, Fréchet wrote:

A set E is called compact if, when {Eⁿ} is a sequence of nomempty, closed subsets of E such that Eⁿ⁺¹ is a subset of Eⁿ for each n, there is at least one element that belongs to all of the Eⁿ’s.

... jai voulu sans doute éviter qu'on puisse appeler compact un noyau solide dense qui n'est agrémenté que d'un fil allant jusqu'à l'infini. C'est une supposition car j'ai complétement oubliè les raisons de mon choix!" [Doubtless I wanted to avoid a solid dense core with a single thread going off to infinity being called compact. This is a hypothesis because I have completely forgotten the reasons for my choice!] (Pier, p. 440)

Fréchet’s "compact" is the modern "relatively sequentially compact," and his "extremal" is today’s "sequentially compact" (Kline, page 1078).

Compact is found in Paul Alexandroff and Paul Urysohn, "Mémoire sur les espaces topologiques compacts," Koninklijke Nederlandse Akademie van Vetenschappen te Amsterdam, Proceedings of the section of mathematical sciences) 14 (1929).

The term COMPANION MATRIX was apparently coined in English by C. C. MacDuffee in The Theory of Matrices (Springer, 1933, reprinted by Chelsea):

A. Loewy [footnote reference] called B (or its negative) a "Begleitmatrix". We shall take the liberty of calling it the companion matrix of the equation f(λ) = 0.

COMPLEMENT (of a set). The OED’s illustrations of non-mathematical uses of complement in the sense of "something which, when added, completes or makes up a whole" go back to 1827. A JSTOR search found the phrases "set complementary to" and "complement" in 1914 in E. W. Chittenden "Relatively Uniform Convergence of Sequences of Functions," Transactions of the American Mathematical Society, 15, 197-201.

COMPLEMENTARY FUNCTION is found in 1841 in D. F. Gregory, Examples of Processes of Differential and Integral Calculus: "As operating factors of the form (d/dx)² + n² very frequently occur in differential equations, it is convenient to keep in mind that the complementary function due to it is of the form C cos nx + C' sin nx [OED].

The term COMPLETE for a space in which all Cauchy convergent sequences are convergent came into general use in the 1920s. Thus the term was not used by Banach in his 1922 paper "Sur les opérations dans les ensembles abstraits et leur application aux équations integrales," but it appears without comment in his Théorie des Operations Linéaires (1932, Introduction, p. 9).

See BANACH SPACE and CAUCHY CONVERGENCE.

COMPLETE INDUCTION (vollständige Induktion) was the term employed by Dedekind in his Was sind und Was sollen die Zahlen? (1887) for what is nowadays called "mathematical induction", and whose "scientific basis" ("wissenschaftliche grundlage") he claimed to have established with his "Theorem of complete induction" (§59). Dedekind also used occasionally the phrase "inference from n to n + 1", but nowhere in his booklet did he try to justify the adjective "complete".

In Concerning the axiom of infinity and mathematical induction (Bull. Amer. Math. Soc. 1903, pp. 424-434) C. J. Keyser referred to "complete induction" as

a form of procedure unknown to the Aristotelian system, for this latter allows apodictic certainty in case of deduction only, while it is just characteristic of complete induction that it yields such certainty by the reverse process, a movement from the particular to the general, from the finite to the infinite.

[the] term "complete induction" used in most continental languages (...) [stress] the contrast with induction in natural science which is incomplete by its very nature, being based on a finite and even relatively small number of experiments.

COMPLETE SOLUTION. The term complete solution or complete integral is due to Lagrange (Kline, page 532).

The term COMPLETENESS was used by Dedekind in 1872, both to describe the closure of a number field under arithmetical operations and as a synonym for "continuity" (Burn 1992).

COMPLETING THE SQUARE. In 1717 in A Treatise of Algebra In Two Books by Philip Ronayne has “Compleating the Square,” “Compleat the Square,” and “Compleating □.” [Google print search, James A. Landau]

The use of the name COMPLEX ANALYSIS to refer to a subject, course or book is fairly new given the long history of the topics it treats. The 1953 textbook Complex Analysis by L. V. Ahlfors appears to have popularised the name. Older names included the theory of function of a complex variable and theory of functions after the German Funktionentheorie. The subject was developed in the 19^th century by French and German mathematicians (Cauchy, Riemann and Weierstrass). English textbooks appeared at the end of the century, notably Harkness & Morley’s A Treatise on the Theory of Functions and Forsyth’s Theory of Functions of a Complex Variable.

The phrase theory of functions of a complex variable appears in German in 1851 as the title of Riemann’s inagural disseration (doctoral disseratation) at Gottingen: “Grundlagen für eine allgemeine Theorie der Functionen einer complexen Veränderlichen Grösse.”

John Aldrich and James A. Landau contributed to this entry. See the entries ANALYSIS and REAL ANALYSIS. Complex analysis terms appear in the analysis list here.

COMPLEX FRACTION is found in English in 1823 in Guy’s Tutor’s assistant, or, Complete school arithmetic by Joseph Guy: "A complex fraction has a fraction, or a mixed number, for its numerator or denominator, or both, as ...." [Google print search]

COMPLEX NUMBER. Most of the 17th and 18th century writers spoke of a + bi as an imaginary quantity. Carl Friedrich Gauss (1777-1855) saw the desirability of having different names for ai and a + bi, so he gave to the latter the Latin expression numeros integros complexos. Gauss wrote:

...quando campus arithmeticae ad quantitates imaginarias extenditur, ita ut absque restrictione ipsius obiectum constituant numeri formae a + bi, denotantibus i pro more quantitatem imaginariam , atque a, b indefinite omnes numeros reales integros inter - et +. Tales numeros vocabimus numeros integros complexos, ita quidem, ut reales complexis non opponantur, sed tamquam species sub his contineri censeatur.

The term complex number was used in English in 1856 by William Rowan Hamilton. The OED2 provides this citation: Notebook in Halberstam & Ingram Math. Papers Sir W. R. Hamilton (1967) III. 657: "a + ib is said to be a complex number, when a and b are integers, and i = [sqrt] -1; its norm is a² + b²; and therefore the norm of a product is equal to the product of the norms of its factors."

COMPOSITE FUNCTION. See the entry CHAIN RULE.

COMPOSITE NUMBER (early meaning). According to Smith (vol. 2, page 14), "The term 'composite,' originally referring to a number like 17, 56, or 237, ceased to be recognized by arithmeticians in this sense because Euclid had used it to mean a nonprime number. This double meaning of the word led to the use of such terms as 'mixed' and 'compound' to signify numbers like 16 and 345." Smith differentiates between "composites" and "articles," which are multiples of 10.

COMPOSITE NUMBER (nonprime number). The OED2 shows numerus compositus Isidore III. v. 7.

Napier used the term numeri compositi.

In 1723 Lexicon Technicum: Or, An Universal English Dictionary of Arts and Sciences, 2nd edition, has:

INCOMPOSITE Numbers, are the same with those Euclid calls Prime Numbers. ... See also in Table XXV. you see that 49031, 49033, and 49037 are all Prime or Incomposite Numbers: But 49039 is a Composite, and 19 is its least Divisor.

COMPUTER. Although computing is associated with calculation, the roots of the words are quite distinct. (See CALCULUS.) Computing has the same Latin root as account for both have to do with reckoning. The OED‘s earliest quotation for compute is from 1631.

The OED has a quotation from 1641 illustrating computer in the sense of a person who does calculations and one from 1897 illustrating computer in the sense of a machine which does calculations.

Since the 1940s these usages have been increasingly displaced and computer has come to refer to what was then a new kind of computing machine. The "Electronic Numerical Integrator and Computer" (ENIAC) was such a machine, although the use of "computer" in its name was not at all innovative. Charles Babbage called the machine he conceived in 1837--one of the ancestors of the modern computer--"the analytical engine."

The term COMPUTER INTENSIVE appears to have entered circulation in the early 1970s. By the end of the decade it was becoming attached to a collection of statistical techniques, including the BOOTSTRAP and CROSS-VALIDATION. A JSTOR search found the term used in this way in Bradley Efron “Computers and the Theory of Statistics: Thinking the Unthinkable,” SIAM Review, 21, (1979), 460-480.

CONCAVE appears in English in 1571 in A Geometricall Practise named Pantometria by Thomas Digges (1546?-1595) [OED].

CONCAVE POLYGON. Fibonacci referred to such a polygon as a figura barbata in Practica geomitrae.

Re-entering polygon is found in 1851 in Problems in illustration of the principles of plane coordinate geometry by William Walton [University of Michigan Historic Math Collection]. Another term is re-entrant polygon.

Concave polygon is found in 1848 in Elements of Plane Geometry, Theoretical and Practical, 3rd edition, by Thomas Duncan: “In a concave polygon, that is, any polygon not convex, the sum of the salient angles together with the defect of each re-entering angle from four right angles, is equal to twice as many right angles as the polygon has sides, wanting four right angles. ... In a convex polygon, the sum of the exterior angles made by producing the sides, is equal to four right angles.” [Google print search, James A. Landau]

CONCHOID (also known as CONCHLOID). Nicomedes (fl. ca. 250 BC) called various curves the first, second, third, and fourth conchoids (DSB). Pappus says that the conchoids were explored by Nicomedes in his work On Conchoid Lines [Michael Fried].

Conchoid is found in English in 1798 in Anti-Jacobin 16 Apr. 181/1: “Ye Conchoids extend.” [OED]

CONCOMITANT VARIABLE in Statistics. See COVARIATE.

CONDITION of a matrix. "The expression ‘ill-conditioned’ is sometimes used merely as a term of abuse applicable to matrices or equations but it seems most often to carry a meaning somewhat similar to that defined below" wrote A. M. Turing in "Rounding-off Errors in Matrix Processes," Quarterly Journal of Mechanics and Applied Mathematics, 1, (1948), p. 297. Evidently the term ill-conditioned was already well established and one of the objects of Turing’s paper was to define measures of ill-conditioning which he called condition numbers. The paper comes from a time when there was great interest in the numerical solution of linear equations and in expressing the process in terms of matrices but the phenomenon of ill-conditioning must have been familiar since the time of Gauss at least. See GAUSSIAN ELIMINATION.

CONDITIONALLY CONVERGENT SERIES. Semi-convergent series appears in 1872 in J. W. L. Glaisher, "On semi-convergent series," Quart. J.

Conditionally convergent series appears in 1890 in The Number-System of Algebra: Treated Theoretically and Historically by Henry B. Fine. Page 55 has “It is important to distinguish between convergent series which remain convergent when all the terms are given the same algebraic signs and [page 56] convergent series which become divergent on this change of signs. Series of the first class are said to be absolutely convergent; those of the second class, only conditionally convergent.” Page 57 has “the terms of a conditionally convergent series can be so arranged that the sum of the series may take any real value whatsoever. In a conditionally convergent series the positive and the negative terms each constitute a divergent series having 0 for the limit of its last term.” [Google print search, James A. Landau]

Conditionally convergent series and semi-convergent series appear in 1893 in A Treatise on the Theory of Functions by James Harkness and Frank Morley: "A series which converges, but does not converge absolutely, is called semi-convergent. ... A convergent series which is subject to the commutative law is said to be unconditionally convergent; otherwise it is said to be conditionally convergent. ... Semi-convergence implies conditional convergence."

CONDITIONAL PROBABILITY Conditional probabilities had been ‘in’ probability since the late 18^th century but there was no standard term meaning conditional probability before the 20^th. Bayes (1763) An Essay towards solving a Problem in the Doctrine of Chances used the expression "the probability of the second [event] on supposition the 1^st happens." For a typical 19^th century presentation see the entry POSTERIOR PROBABILITY.

The expression "conditional probability" appears in 1937 in the very technical setting of J. L. Doob’s "Stochastic Processes Depending on a Continuous Parameter," Transactions of the American Mathematical Society, 42, (1937) and in the more elementary discussion of J. V. Uspensky’s Introduction to Mathematical Probability:

Let A and B be two events whose probabilities are (A) and (B). It is understood that the probability (A) is determined without any regard to B when nothing is known about the occurrence or nonoccurrence of B. When it is known that B occurred, A may have a different probability, which we shall denote by the symbol (A, B) and call 'conditional probability of A, given that B has actually happened.' (page 31)

This entry was contributed by John Aldrich. A citation was provided by James A. Landau. See also SYMBOLS IN PROBABILITY on the Symbols in Probability and Statistics page.

CONE is defined in Euclid’s Elements, XI, def.18, and it appears in a mathematical context in the presocratic atomist Democritus of Abdera, who wrote:

If a cut were made through a cone parallel to its base, how should we conceive of the two opposing surfaces which the cut has produced -- as equal or as unequal? If they are unequal, that would imply that a cone is composed of many breaks and protrusions like steps. On the other hand if they are equal, that would imply that two adjacent intersection planes are equal, which would mean that the cone, being made up of equal rather than unequal circles, must have the same appearance as a cylinder; which is utterly absurd (D. V. 55 B 155, translation by Philip Wheelwright in The Presocratics, Indianapolis: The Bobbs-Merrill Company, Inc., 1960, p.183).

[This entry was contributed by Michael Fried.]

CONFIDENCE INTERVAL. Interval statements about parameters go back a very long way and have taken several distinct forms. Hald (1998, pp. 23-4) finds a BAYESIAN analysis in Laplace’s "Mémoire sur la Probabilité des Causes par les événements," Savants étranges, 6, (1774), p. 621-656. Oeuvres 8, pp. 27-65 (English translation and commentary by S. M. Stigler in Statistical Science, 1, (1986), 359-378) and a non-Bayesian analysis in Lagrange’s "Mémoire sur l'Utilité de la Méthode de Prendre le Milieu entre les Résultats de Plusieurs Observations," Misc. Taurinensia, 5, (1776), pp. 167-232. Oeuvres 2, pp. 173-234. Both were concerned with the probability of a success in Bernoulli trials.

The idea of a FIDUCIAL interval appeared in 1930 in R. A. Fisher’s "Inverse Probability," Proceedings of the Cambridge Philosophical Society, 26, 528-535.

Jerzy Neyman (1894-1981) launched the modern theory of confidence intervals and introduced the term in the 1934 paper, "On the Two Different Aspects of the Representative Method," Journal of the Royal Statistical Society, 97, 558-625:

The form of this solution consists in determining certain intervals, which I propose to call the confidence intervals..., in which we may assume are contained the values of the estimated characters of the population, the probability of an error is a statement of this sort being equal to or less than 1 - ε, where ε is any number 0 < ε < 1, chosen in advance. The number ε I call the confidence coefficient.

The term CONFLUENT HYPERGEOMETRIC FUNCTION was introduced by E. T. Whittaker and G. K. Watson in the 1915 edition of A Course of Modern Analysis writes G. F. J. Temple “Edmund Taylor Whittaker,” Biographical Memoirs of Fellows of the Royal Society of London, 2, (1956), p. 307.

CONFORMAL MAPPING. The term projectio conformis was introduced by F. T. Schubert in 1789 (DSB, article: "Euler").

Gauss used the term conforme Abbildung.

Cayley used the term orthomorphosis.

In 1956, Albert A. Bennett wrote: "Thus a function of one argument, or a mapping, is simply a one-valued, two-term relation. The term 'mapping' thus includes 'functional,' 'projectivity,' and so forth. Although the phrase 'conformal mapping' is old, the general use here mentioned is very recent and may be due to van der Waerden, 1937." (This quotation was taken from "Concerning the function concept," The Mathematics Teacher, May 1956.)

CONFOUNDING has been in the vocabulary of the theory of experimental design from the beginning. "Confounded" appears on p. 513 of R. A. Fisher’s "The Arrangement of Field Experiments" Journal of the Ministry of Agriculture of Great Britain, 33: 503-513 (1926). But the usage is older than the modern theory. In his System of Logic (1843) John Stuart Mill wrote that in devising an experiment "We require also that none of the circumstances [of the experiment] that we do know shall have effects susceptible of being confounded with those of the agents whose properties we wish to study." (Book III, chapter X.)

(based on David (2001) and S. Greenland "Confounding" in Encyclopedia of Biostatistics 1, (1998), 900-907. Chichester: Wiley

CONGRUENT (geometric figures). Congruere (Latin, "to coincide") was used by geometers of the sixteenth century in their editions of Euclid in quoting Common Notion 4: "Things which coincide with one another are equal to one another." ["Ea ... aequalia sunt, quae sibi mutuo congruunt."]

For instance, in 1539, Christoph Clavius (1537?-1612) writes:

...Hinc enim fit, ut aequalitas angulorum ejusdem generis requirat eandem inclinationem linearum, ita ut lineae unius conveniant omnino lineis alterius, si unus alteri superponatur. Ea enim aequalia sunt, quae sibi mutuo congruunt.

[Cf. page 363 of Clavius’s "Euclidis", vol. I, Romae: Apvd Barthdomaevm Grassium, 1589]

As a more technical term for a relation between figures, congruent seems to have originated with Gottfried Wilhelm Leibniz (1646-1716), writing in Latin and French. His manuscript "Characteristica Geometrica" of August 10, 1679, is in his Gesammelte Werke, dritte Folge: mathematische Schriften, Band 5. On p. 150 he says that if a figure can be applied exactly to another without distortion, they are said to be congruent:

Quodsi duo non quidem coincidant, id est non quidem simul eundem locum occupent, possint tamen sibi applicari, et sine ulla in ipsis per se spectatis mutatione facta alterum in alterius locum substitui queat, tunc duo illa dicentur esse congrua, ut A.B et C.D in fig.39 ...

Shortly afterwards, on September 8, 1679, he included a similar definition in a letter to Hugens (sic) van Zulichem. In his ges. Werke etc. as above, volume 2, p. 22, he illustrates congruence with a pair of triangles, and says that they "peuvent occuper exactement la meme place, et qu'on peut appliquer ou mettre l'un sur l'autre sans rien changer dans ces deux figures que la place." [Ken Pledger and Julio González Cabillón]

Writers commonly refer to geometric figures as equal as recently as the nineteenth century. In 1828, Elements of Geometry and Trigonometry (1832) by David Brewster (a translation of Legendre) has:

Two triangles are equal, when an angle and the two sides which contain it, in the one, are respectively equal to an angle and the two sides which contain it, in the other.

CONGRUENT (in modular arithmetic) was defined by Carl Friedrich Gauss (1777-1855) in 1801 in Disquisitiones arithmeticae: "Si numerus a numerorum b, c differentiam metitur, b et c secundum a congrui dicuntur."

Congruent is found in English in 1808 in The Monthly Review; or Literary Journal, Enlarged. A review of Gauss’s Arithmetical Researches (specifically a review of Poullet Delisle’s French translation Récherches Arithmétiques of the original work by “M. Ch. Fr. Gauss, of Brunswick”.

M. Gauss begins with new names and new signs. If a number a divides the difference of b and c, then b and c are said to be congruous (congrus) according to a, which is called the modulus. The sign appropriate to this congruity is ≡, so that, in this new symbolical language,

b ≡ c (modulus a).

The numbers b and c are called residues, (residus,) b the residue of c, and c the residue of b, to the modulus a. For instance, -16 and 9 are congruous to the modulus 5; or, symbolically,

-16 ≡ 9 (mod. 5).

On the same page the reviewer writes:

Here we cannot forbear expressing our wish that M. Gauss had not been tempted into the invention of new names and new signs: for, as far as our experience goes, the formation and employment of them in this work have certainly not elucidated the reasonings, and very slightly abridged them. Indeed, the mental labour of the reader (and that is an object which an author ought to consult) is rendered greater: not because these new names and new signs are difficult of explanation; but because they are not familiar: so that, besides the usual impediments of abstruse mathematical processes, the author has contrived to add these artificial impediments; and indeed, in the conduct and explanation of his processes, he seldom consults the ease of his reader.

[Google print search, James A. Landau]

See MODULUS, MODULO and MOD.

CONIC SECTION. Apollonius of Perga wrote a work in 8 books, of which the first 4 have survived in the original Greek and books 5 through 7 in Arabic translation.  Book 8 is lost.  This work is referred to in English as Conic Sections or Conics.

www.wilbourhall.org/pdfs/Apollonius_VOL_I.pdf  gives Apollonius’s work in an 1890 Greek reprint and in Latin translation.  The Latin title is Conicorum and the Greek title is (in all capitals) “ΚΟΝΙΚΟΝ.” Many sources transliterate this name as Keonikon.

The Muslim mathematician Abu Ali Hasan Ibn al-Haitham, also known by his Latinized name Alhazen or Alhacen, wrote a book whose title in English is Treatise on the Completion of [Appolonius’s] Conics.  The Arabic title is Kitab al-makhrutat (German scholars transliterate it as Maqealah fei tameam kiteab al-makhreurteart).  Perhaps al-makhrutat is the Arabic term for the conic sections.

The first Latin translation (from the Arabic) of al-Haytham’s work was in 1661, from an Arabic copy found in the di Medici library by Giovanni Alfonso Borelli.  The translation was by Abraham Ecchellensis.

Conic section is found in the title De sectionibus conicis by Claude Mydorge (1585-1647).

The term is also found in the title Essay on Conic Sections by Blaise Pascal (1623-1662) published in February 1640.

[James A. Landau]

CONJECTURE in the sense of "an opinion or supposition based on evidence which is admittedly insufficient" had been in English for a more than a century when Isaac Newton used the term in 1672: "I shall refer him to my former Letter, by which that conjecture will appear to be ungrounded." Mr. Isaac Newtons Answer to Some Considerations upon His Doctrine of Light and Colors; Which Doctrine Was Printed in Numb. 80. of These Tracts, Phil. Trans. VII. p. 5084. The conjecture in question seemed to concern optics, not mathematics.

Jacob Steiner (1796-1863) referred to a result of Poncelet as a conjecture. Poncelet showed in 1822 that in the presence of a given circle with given center, all the Euclidean constructions can be carried out with ruler alone (DSB, article: "Mascheroni").

In Récréations Mathématiques, tome II, Note II, Sur les nombres de Fermat et de Mersenne (1883), É. Lucas referred to "la conjecture de Fermat."

In his article "Conjecture" (Synthese 111, pp. 197-210, 1997), Barry Mazur writes (bottom of page 207):

Since I am not a historian of Mathematics I dare not make any serious pronouncements about the historical use of the term, but I have not come across any appearance of the word Conjecture or its equivalent in other languages with the above meaning [i.e., an opinion or supposition based on evidence which is admittedly insufficient] in mathematical literature except in the twentieth century. The earliest use of the noun conjecture in mathematical writing that I have encountered is in Hilbert’s 1900 address, where it is used exactly once, in reference to Kronecker’s Jugendtraum.

CONJUGATE. Augustin-Louis Cauchy (1789-1857) used conjuguées for a + bi and a - bi in Cours d'Analyse algébrique (1821, p. 180) (Smith vol. 2, page 267).

CONJUGATE ANGLE is found in "The Genesis of Quaternions" by John Paterson in the Cambridge and Dublin Mathematical Journal of 1854. [Google print search]

CONJUGATE PRIOR DISTRIBUTIONS. The term and supporting theory appeared in Howard Raiffa and Robert Schlaifer’s Applied Statistical Decision Theory, (1961). (David 2001.) The same theory was developed independently by G. A. Barnard; he described the distributions involved as being "closed under sampling." Barnard’s work is reported by G. B. Weatherill "Bayesian Sequential Analysis," Biometrika, 48, (1961), 281-292.

CONJUNCTION. According to W. & M. Kneale The Development of Logic (1962) p. 160, conjunction was discussed by the Stoic logicians. "They defined a conjunctive proposition as one which was true if both the conjoined propositions were true and otherwise false." For general information on the Stoics see Dick Baltzly Stoicism.

For the English words conjunction and conjunctive, the OED’s earliest quotations are from the 19^th century, beginning with (from c1848) Sir William Hamilton Logic II. App. 369 "The Conjunctive and Disjunctive forms of Hypothetical reasoning are reducible to immediate inferences."

CONSERVATIVE EXTENSION. Martin Davis believes the term was first used by Paul C. Rosenbloom. It appears in The Elements of Mathematical Logic, 1st ed., New York: Dover Publications, 1950.

CONSISTENCY. The term consistency applied to estimation was introduced by R. A. Fisher in " On the Mathematical Foundations of Theoretical Statistics. " (Phil. Trans. R. Soc. 1922). Fisher wrote: "A statistic satisfies the criterion of consistency, if, when it is calculated from the whole population, it is equal to the required parameter." (p. 309)

In the modern literature this notion is usually called Fisher-consistency (a name suggested by Rao) to distinguish it from the more standard notion linked to the limiting behavior of a sequence of estimators. The latter is hinted at in Fisher’s writings but was perhaps first set out rigorously by Hotelling in the "The Consistency and Ultimate Distribution of Optimum Statistics," Transactions of the American Mathematical Society (1930). [This entry was contributed by John Aldrich, based on David (1995).]

CONSTANT was introduced by Gottfried Wilhelm Leibniz (1646-1716) (Kline, page 340).

Constant is used as a noun in English in 1832 in the title Treatise on Strength, Flexure, and Stiffness of Cast-Iron Beams and Columns, with Tables of Constants by W. Turnbull. [OED]

CONSTANT OF INTEGRATION. In 1807 Hutton Course Math. has: "To Correct the Fluent of any Given Fluxion .. The finding of the constant quantity c, to be added or subtracted with the fluent as found by the foregoing rules, is called correcting the fluent.

In 1831 Elements of the Integral Calculus (1839) by J. R. Young refers to "the arbitrary constant C."

Constant of integration is found in 1846 in "On the Rotation of a Solid Body Round a Fixed Point" by Arthur Cayley in the Cambridge and Dublin Mathematical Journal [University of Michigan Historical Math Collection].

In 1849 in An Introduction to the Differential and Integral Calculus, 2nd ed., by James Thomson, it is called the "constant quantity annexed."

CONTINGENCY TABLE was introduced by Karl Pearson in "On the Theory of Contingency and its Relation to Association and Normal Correlation," which appeared in Drapers' Company Research Memoirs (1904) Biometric Series I:

This result enables us to start from the mathematical theory of independent probability as developed in the elementary text books, and build up from it a generalised theory of association, or, as I term it, contingency. We reach the notion of a pure contingency table, in which the order of the sub-groups is of no importance whatever.

The CONTINUED FRACTION was introduced by John Wallis (1616-1703) (DSB, article: "Cataldi").

Wallis used continue fracta in 1655 in Arithmetica Infinitorum Prop. CXCI.

The phrase "Esto igitur fractio eiusmode continue fracta quaelibet sic deignata..." is found in volume I of Opera Mathematica, a collection of Wallis' mathematical and scientific works published in 1693-1699.

The phrase "fractio, quae denominatorem habeat continue fractum" is found in Opera, I, 469 (Smith vol. 2, page 420).

In 1685 Wallis referred to Brouncker’s continued fraction as "a fraction still fracted continually" in A Treatise of Algebra [Philip G. Drazin, David Fowler, James A. Landau, Siegmund Probst].

Continued fraction is found in English in 1742 in The Elements of Algebra in a New and Easy method by Nathaniel Hammond: “...for it is the same thing whether the Quantities that compose the Numerator, are placed successively one after another like one continued Fraction, or placed separately and distinctly, like different Fractions....” [Google print search, James A. Landau]

CONTINUOUS. The term continuous has been in the vocabulary of mathematics for more than 250 years but in that time its meaning has changed. The earliest definition given by Katz (page 524) is from the second volume of Euler’s Introductio in analysin infinitorum (1748), "A continuous curve is one such that its nature can be expressed by a single function of x. If a curve is of such a nature that for its various parts ... different functions of x are required for its expression... then we call such a curve discontinuous."

However modern usage is closer to the definitions given by Bernard Bolzano in 1817 and Augustin-Louis Cauchy in 1821. (Katz page 641) Cauchy wrote "The function f(x) will be, between two assigned values of the variable x, a continuous function of this variable if for each value of x between these limits, the [absolute] value of the difference f(x + α) - f(x) decreases indefinitely with α." Cours d'analyse (Oeuvres II.3), p. 43.

In English mathematical writing of the nineteenth century the term continuous often seemed to mean smooth and without discontinuity, where a discontinuity might be a corner as well as what would be classified as a discontinuity today. A JSTOR search found Thomas Knight writing about bodies being bounded by continuous curve surfaces in his "Of the Attraction of Such Solids as are Terminated by Planes; and of Solids of Greatest Attraction," Philosophical Transactions of the Royal Society, 102, (1812), 247-309 and meaning surfaces without corners. In 1893 the OED gave the following definition of a continuous function, "a function that varies continuously, and whose differential coefficient therefore never becomes infinite." Amazingly it is still there today.

Turning to calculus textbooks, Todhunter’s A treatise on the differential calculus with numerous examples (8^th edition 1878, p. 71) states, "the function must have a single finite value for every value of the variable, and the function must change gradually as the variable passes from one value to the other so that, corresponding to any indefinitely small change in the value of the variable there must be an indefinitely small change in the function." In the early 20^th century G. H. Hardy wrote in his A course of pure mathematics (1908, p. 172) "The function φ(x) is said to be continuous for x = ξ if it tends to a limit as x tends to ξ from either side, and each of these limits is equal to φ(ξ)."

In the 20^th century the notion of a continuous function between abstract spaces came into use. There is a definition of a continuous function from one topological space to another in Felix Hausdorff’s Grundzüge der Mengenlehre (1914, p. 359).

See also ABSOLUTE CONTINUITY, UNIFORM CONTINUITY.

[This entry was contributed by John Aldrich.]

CONTINUOUS CURVE is found in English in 1830 in The Edinburgh Encyclopaedia in the article on “Epicycloid”: “If the generating circle be supposed to continue to roll along the base produced, in each case the generating point will describe other cycloids, exactly like the first. In fact, they may be considered as forming with it a continuous curve, which never returns into itself, but goes on indefinitely.” [Google print search, James A. Landau]

CONTINUOUS FUNCTION is found in English in 1836 in The Differential and Integral Calculus by Augustus de Morgan. According to James A. Landau, there are at least nine usages of continuous function and 34 of the word continuous but there does not seem to be a definition of continuous function.

CONTINUUM. According to the DSB, the term continuum appeared as early as the writings of the Scholastics, but the first satisfactory definition of the term was given by Cantor.

CONTINUUM HYPOTHESIS. In his 1900 Paris lecture, Hilbert titled his first problem “Cantor’s Problem of the Power of the Continuum.”

In his 1901 doctoral dissertation writen under Hilbert, Felix Bernstein used the term "Cantor’s Continuum Problem" ("das Cantorsche Continuumproblem"). This is the first time the term "Cantor’s Continuum Problem" appeared in print, according to Cantor’s Continuum Problem by Gregory H. Moore, which also states that "presumbly Bernstein obtained the name 'Continuum Problem' by abbreviating Hilbert’s title."

Continuum problem also appears in Felix Bernstein, "Zum Kontinuumproblem," Mathematische Annalen 60 (1905); Julius König, "Zum Kontinuum-Problem," Verhandlungen des dritten internat. Math.- Kongress (1905); and Julius König, "Zum Kontinuumproblem," Mathematische Annalen 60 (1905).

In his essay "On the Infinite" (1925) Hilbert referred to the question of whether continuum hypothesis is true as the "famous problem of the continuum"; the word "hypothesis" is not used. Two years later, in "The foundations of mathematics" (1927) he referred to "the proof or refutation of Cantor’s continuum hypothesis."

Carlos César de Araújo believes that the use of "hypothesis" here became more popular and well-established only after the 1934 monograph of Sierpinski, "Hypothése du continu."

In the 1962 Chelsea translation of the 1937 3rd German edition of Hausdorff’s Mengenlehre pp 45f is the following:

A conjecture that was made at the beginning of Cantor’s investigations, and that remains unproved to this day, is that [alef] is the cardinal number next larger than [alef-null]; this conjecture is known as the continuum hypothesis, and the question as to whether it is true or not is known as the problem of the continuum

Continuum hypothesis appears in Waclaw Sierpinski, “Sur deux propositions, dont l'ensemble équivaut à l'hypothése du conntinu”, Fundamenta Mathematicae 29, pp 31-33 (1937).

Continuum hypothesis appears in the title "The consistency of the axiom of choice and of the generalized continuum-hypothesis" by Kurt Gödel, Proc. Nat. Acad. Sci., 24, 556-557 (1938) [James A. Landau, Carlos César de Araújo].

CONTRACTION MAPPING FIXED-POINT THEOREM. This appears as Theorem 6 on p. 140 of Stefan Banach’s “Sur les opérations dans les ensembles abstraits et leur application aux équations integrales”, Fundamenta Mathematicae, 3, (1922), 133-181. The theorem is sometimes called Banach’s fixed point theorem.

CONTRAPOSITIVE. Boethius wrote: " Est enim per contrapositionem conversio, ut si dicas omnis homo animal est, omne non animal non homo est."

Contraposition is found in English in 1551 in T. Wilson, Logike: "A conuersion by contraposition is when the former part of the sentence is turned into the last rehearsed part, and the last rehearsed part turned into the former part of the sentence, both the propositions being uniuersall, and affirmatiue, sauing that in the second proposition there be certaine negatiues enterlaced" [OED].

Contrapose and contraposite are other older terms in English.

De Morgan used the adverb contrapositively in 1858 in Trans. Camb. Philos. Soc. [OED].

Contrapositive appears as an adjective in the preface to The Elements of Plane Geometry (1868) by R. P. Wright. The preface was written by T. A. Hirst (1830-1892): "The two theorems are, in fact, contrapositive forms, one of the other; the truth of each is implied, when that of the other is asserted, and to demonstrate both geometrically is more than superfluous; it is a mistake, since the true relation between the two is thereby masked."

Contrapositive was used as a noun in 1870 by William Stanley Jevons in Elementary Lessons in Logic (1880): "Convert and show that the result is the contrapositive of the original" [OED].

CONTRA-POSITIVE. In 1835 in Theory of Conjugate Functions, or Algebraic Couples, William Rowan Hamilton uses this term to mean “negative” (in the sense of negative numbers in algebra). [Google print search, James A. Landau]

CONTROL CHART. W. A. Shewhart devised this basic tool of quality control in the 1920s but the technique (and the name) only came into general use following the publication of his book Economic Control of Quality of Manufactured Product in 1931.

See the entry QUALITY CONTROL.

CONVERGENCE (of a vector field) was coined by James Clerk Maxwell (Katz, page 752; Kline, page 785). It is the negative of the divergence, q.v.

See CURL.

The terms CONVERGENT and DIVERGENT were used by James Gregory in 1667 in his Vera circuli et hyperbolae quadratura (Cajori 1919, page 228). Gregory wrote series convergens.

However, according to Smith (vol. 2, page 507), the term convergent series is due to Gregory (1668) and the term divergent series is due to Nicholas I Bernoulli (1713). In a footnote, he cites F. Cajori, Bulletin of the Amer. Math. Soc. XXIX, 55.

CONVERSE is first found in English in Sir Henry Billingsley’s 1570 translation of Euclid’s Elements [OED].

CONVEX (curved outward) appears in English in 1571 in A Geometricall Practise named Pantometria by Thomas Digges (1546?-1595) [OED].

CONVEX FUNCTION. A. Guerraggio and E. Molho write, "The first modern formalization of the concept of convex function appears in J. L. W. V. Jensen ‘Om konvexe funktioner og uligheder mellem midelvaerdier,’ Nyt Tidsskr. Math. B 16 (1905), pp. 49-69. Since then, at first referring to ‘Jensen’s convex functions,’ then more openly, without needing any explicit reference, the definition of convex function becomes a standard element in calculus handbooks." ("The Origins of Quasi-concavity: a Development between Mathematics and Economics," Historia Mathematica, 31,  (2004), 62-75.)

The term quasi-convex function was introduced by W. Fenchel in his Convex Cones, Sets and Functions (1953). See Guerraggio & Molho (op. cit.) who also describe earlier appearances of the concept in work by von Neumann (1928) and de Finetti (1949). The term quasi-concave function appears in K. J. Arrow & G. Debreu "Existence of an Equilibrium for a Competitive Economy," Econometrica, 22, (1954), pp. 265-290.

See also JENSEN’S INEQUALITY.

CONVEX POLYGON. In 1828 in Elements of Geometry and Trigonometry (1832) by David Brewster (a translation of Legendre) is found the following:

We thought it better to restrict our reasoning to those lines which we have named convex, and which are such that a straight line cannot cut them in more than two points.

Convex polygon is found in 1848 in Elements of Plane Geometry, Theoretical and Practical, 3rd edition, by Thomas Duncan: “In a concave polygon, that is, any polygon not convex, the sum of the salient angles together with the defect of each re-entering angle from four right angles, is equal to twice as many right angles as the polygon has sides, wanting four right angles. ... In a convex polygon, the sum of the exterior angles made by producing the sides, is equal to four right angles.” [Google print search, James A. Landau]

In 1857 Mathematical Dictionary and Cyclopedia of Mathematical Sciences has convex polygon and the synonymous term salient polygon.

See also SALIENT ANGLE.

CONVEX SET. The German term appears in E. Steinitz "Bedingt konvergente Reihen und konvexe Systeme, I," J. Reine Angew. Math., 143, (1913) 128-175. A JSTOR search found the term in English in J. L. Walsh "On the Transformation of Convex Point Sets," Annals of Mathematics, 22, (1921), 262-266.

In the early 20^th century convolutions appeared in the field of INTEGRAL EQUATIONS. In his 1906 paper “Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen. Vierte Mittelung” Nachrichten von d. Königl. Ges. d. Wissensch. zu Göttingen (Math.-physik. Kl.) (1906) 157-227 Hilbert used the word Faltung, meaning “folding” or “plaiting.” See J. Dieudonné History of Functional Analysis (pp. 113-4). The term became standard in the new field of FUNCTIONAL ANALYSIS.

In the 1930s an English equivalent was found. In 1932 Aurel Wintner used “folding expression” in his “Remarks on the Ergodic Theorem of Birkhoff,” Proceedings of the National Academy of Sciences, 18, (3), p. 251. Norbert Wiener stuck to Faltung in his 1933 book, The Fourier Integral and Certain of its Applications, maintaining that “there is no good English word” (p. 45) Actually there was a rarely used and rather formal English synonym for “folding” and Wintner used “convolution” in his 1934 article, “On Analytic Convolutions of Bernoulli Distributions,” American Journal of Mathematics, 56, p. 662. This became the usual English term. See the Encyclopaedia of Mathematics entry.

[This entry was contributed by John Aldrich. A citation was provided by Yaakov Stein.]

The word COORDINATE was introduced by Gottfried Wilhelm Leibniz (1646-1716). He also used the term axes of co-ordinates. According to Cajori (1919, pages 175 and 211), he used the terms in 1692; according to Ball, he used the terms in a paper of 1694. Bill Stockich has found a use by Leibniz in a manuscript dated April-May 1673. See page 229. Stockich writes that this manuscript “may be among Leibniz’s private papers when he was in the early stages of learning the subject, but it does indicate to me that he had been accustomed to using the word long before he did in the Acta Eruditorum.”

Leibniz used the term in "De linea ex lineis numero infinitis ordinatim ductis inter se concurrentibus formata, easque omnes tangente, ac de novo in ea re Analysis infinitorum usu," in Acta Eruditorum, vol. 11 (1692), pp. 168-171. On p. 170: "Verum tam ordinata quam abscissa, quas per x & y designari mos est (quas & coordinatas appellare soleo, cum una sit ordinata ad unum, altera ad alterum latus anguli, a duabus condirectricibus comprehensi) est gemina seu differentiabilis." The article is also printed in Leibniz, Mathematische Schriften (ed. Gerhardt), vol. 5, pp. 266-269 [Siegmund Probst].

Descartes did not use the term coordinate (Burton, page 350).

The term COORDINATE GEOMETRY is dated 1815-25 in RHUD2. An early use of the term is by Matthew O'Brien (1814-1855) in A treatise on plane co-ordinate geometry; or, The application of the method of co-ordinates to the solution of problems in plane geometry, Part 1, Cambridge: Deighton, 1844.

COPLANAR appears in Sir William Rowan Hamilton, Lectures on Quaternions (London: Whittaker & Co., 1853): "In that particular case, there was ready a known signification [36] for the product line, considered as the fourth proportional to the unit-line (assumed here on the last-mentioned axis), and to the two coplanar factor-lines" [James A. Landau].

CORNISH-FISHER EXPANSION. The technique is described in E. A. Cornish and Fisher, R. A. "Moments and Cumulants in the Specification of Distributions." Revue de l'Institute International de Statistique, 4, 1-14, 1937.  A JSTOR search found the phrase "Cornish-Fisher expansion" used in L. A. Aroian "On the Levels of Significance of the Incomplete Beta Function and the F-Distributions," Biometrika, Vol. 37, No. 3/4. (Dec., 1950), pp. 219-223.

COROLLARY. From the Latin corolla, a small garland. The word is dated 14th century by Merriam-Webster.

The word is found in English in 1669 in Philosophical Transactions: Giving Some Accompt of the Present Undertakings, Studies and Labours of the Ingenious in Many Considerable Parts of the World, Vol. III For Anno 1668: “And as a Corollary of Prop. 62, he Cubeth or measureth either of the Segments of a Parabolical Conoid cut with a Plain, parallel to the Axis.” [Google print search, James A. Landau]

In an essay entitled "The Essence of Mathematics" (see James R. Newman’s anthology The world of mathematics), Charles Saunders Peirce (1839-1914) wrote:

(...) while all the "philosophers" follow Aristotle in holding no demonstration to be thoroughly satisfactory except what they call a "direct demonstration", or a "demonstration why" (...) the mathematicians, on the contrary, entertain a contempt for that style of reasoning, and glory in what the philosophers stigmatize as "mere indirect demonstrations", or "demonstrations that". Those propositions which can be deduced from others by reasoning of the kind that the philosophers extol are set down by mathematicians as "corollaries". That is to say, they are like those geometrical truths which Euclid did not deem worthy of particular mention, and which his editors inserted with a garland, or corolla, against each in the margin, implying perhaps that it was to them that such honor as might attach to these insignificants remarks was due. (...) we may say that corollarial, or "philosophical" reasoning is reasoning with words; while theorematic, or mathematical reasoning proper, is reasoning with specially constructed schemata.

[Carlos César de Araújo]

CORRELATION, CORRELATION COEFFICIENT and COEFFICIENT OF CORRELATION. Francis Galton was the first to measure correlation. The index of co-relation appears in 1888 in his "Co-Relations and Their Measurement," Proc. R. Soc., 45, 135-145: "The statures of kinsmen are co-related variables; thus, the stature of the father is correlated to that of the adult son,..and so on; but the index of co-relation ... is different in the different cases" [OED]. "Co-relation" soon gave way to "correlation" as in W. F. R. Weldon’s "The Variations Occurring in Certain Decapod Crustacea-I. Crangon vulgaris," Proc. R. Soc., 47, (1889 - 1890), 445-453.

The term coefficient of correlation was apparently originated by Edgeworth in 1892, according to Karl Pearson’s "Notes on the History of Correlation," (reprinted in Pearson & Kendall (1970). It appears in 1892 in F. Y. Edgeworth, "Correlated Averages," Philosophical Magazine, 5th Series, 34, 190-204.

The OED2 shows Pearson using coefficient of correlation in 1896 in Contributions to the Mathematical Theory of Evolution. Note on Reproductive Selection, Proc. R. Soc., 59, p. 302: "Let r₀ be the coefficient of correlation between parent and offspring." But both correlation-coefficient and correlation coefficient appear in another 1896 paper by Pearson, "Mathematical Contributions to the Theory of Evolution.  III. Regression, Heredity and Panmixia," Phil. Trans. R. Soc., Ser. A. 187, 253-318. This paper introduced the product moment formula for estimating correlations--Galton and Edgeworth had used different methods.

Partial correlation. G. U. Yule introduced "net coefficients" for "coefficients of correlation between any two of the variables while eliminating the effects of variations in the third" in "On the Correlation of Total Pauperism with Proportion of Out-Relief" (in Notes and Memoranda) Economic Journal, Vol. 6, (1896), pp. 613-623. Pearson argued that partial and total are more appropriate than net and gross in Karl Pearson & Alice Lee "On the Distribution of Frequency (Variation and Correlation) of the Barometric Height at Divers Stations," Phil. Trans. R. Soc., Ser. A, 190, (1897), p. 462n. Yule went fully partial with his 1907 paper "On the Theory of Correlation for any Number of Variables, Treated by a New System of Notation," Proc. R. Soc. Series A, 79, pp. 182-193.

Multiple correlation. At first "multiple correlation" referred only to the general approach, e.g. by Yule in Economic Journal (1896). The coefficient arrives later. "On the Theory of Correlation" (J. Royal Statist. Soc., 1897, p. 833) refers to a coefficient of double correlation R₁ (the correlation of the first variable with the other two). Yule (1907, p. 193) discussed the "coefficient of n-fold correlation," written R_1(23...n). Pearson used the phrases "coefficient of multiple correlation" in his 1914 "On Certain Errors with Regard to Multiple Correlation Occasionally Made by Those Who Have not Adequately Studied this Subject," Biometrika, 10, 181-187, and "multiple correlation coefficient" in his 1915 paper "On the Partial Correlation Ratio," Proc. R. Soc. Series A, 91, 492-498.

This entry was contributed by John Aldrich. See also FISHER’S z TRANSFORMATION OF THE CORRELATION COEFFICIENT and the discussion on probability and statistics symbols on the mathematical symbols page.

The term CORRELOGRAM was introduced by H. Wold in 1938 (A Study in the Analysis of Stationary Time Series). There is a plot of empirical serial correlations, i.e. an empirical correlogram, in Yule’s "Why Do We Sometimes Get Nonsense Correlations between Time-series ..." Journal of the Royal Statistical Society, 89, (1926), 1-69 (David 2001).

CORRESPONDENCE ANALYSIS (Statistics). This method for analysing discrete multivariate data was proposed in 1935 by H. O. Hirschfeld (Hartley) "A Connection between Correlation and Contingency," Proceedings of the Cambridge Philosophical Society, 31, (1935) 520-4. Since then it has been rediscovered several times and given a variety of names. "Correspondence analysis" has become the standard term following the work of J.-P. Benzécri Analyse des données, tome 2: analyse des correspondances. (1973). (From M. O. Hill’s article "Correspondence Analysis" in Encyclopedia of the Statistical Sciences 2, 204-210.)

COSECANT. The cosecant was called the secans secunda by Magini (1592) and Cavalieri (1643) (Smith vol. 2, page 622).

Co-secant is found in English in 1658 in Trigonometria Britannica by John Newton: “And as the co-tangents are made from the Tangents, so are the Secants to be made from the sines, For as the sine of an Arch, is to Radius, so is Radius to the co-secant of that Arch by the 31th of the first.” [Glen Van Brummelen].

Some sources say the word cosecant was introduced by Edmund Gunter (1581-1626). However, he apparently did not use the term. Ball (page 243) and Smith (vol. 2, page 622) say the term cosecant seems to have been first used by Rheticus, reporting that the Latin cosecans appears in Opus Palatinum de triangulis ("The Palatine Work on Triangles"), which was written by Georg Joachim von Lauchen Rheticus (1514-1574). This treatise was published after his death by his pupil Valentin Otto in 1596. Ball wrote “I think” it came from Rheticus, and Smith probably took the information from Ball. However, Glen Van Brummelen, in an email in 2014, reports that looking at Opus palatinum he cannot find the term.

COSET was used in 1910 by G. A. Miller in Quarterly Journal of Mathematics. [OED]

COSINE. While the SINE was discussed and named by mathematicians writing in Sanskrit and Arabic, the naming of cosine was the work of Europeans writing in Latin.

According to Smith vol. 2, page 619, the emergence of a special term began with Plato of Tivoli (c. 1120) and his use of the expression chorda residui. The Latin word chorda was actually a better translation of the Sanskrit-Arabic word for SINE than the word chosen, sinus, but once the latter came into use most mathematicians chose a term for cosine based upon it. The examples Smith gives are sinus rectus complementi from Regiomontanus (c. 1463), basis (exceptionally) from Rhaeticus (1551), sinus rectus secundus, sinus residuae from Vieta (1579), and sinus secundus from Magini (1609). Glen Van Brummelen found an earlier use for sinus rectus secundus than Smith gives, namely by Peter Apian, who used the phrase for cosine in his 1541 Instrumentum sinuum seu primi mobilis.

The term co.sinus was suggested by the English mathematician Edmund Gunter (1581-1626) in his Canon triangulorum, sive, Tabulae sinuum et tangentium artificialium ad radium 100000.0000. & ad scrupula prima quadrantis (1620). According to Smith (page 619), the term was "soon modified by John Newton (1658) into cosinus, a word which was thereafter received with general favor."

The OED finds cosine in English in a passage from 1635: “As the Radius Is to the cosine of the angle given.” This comes from John Wells Sciographia, or the art of shadowes : Plainly demonstrating out of the Sphere, how to project both great and small circles, upon any plane whatsoever: with a new conceit of reflecting the sunne beames upon a diall ... All performed, by the doctrine of Triangles.

COTANGENT. Bradwardine used the term umbra recta.

Magini (1609) used tangens secunda.

Cotangent was coined in Latin by Edmund Gunter (1581-1626) in 1620 in Canon Triangulorum, or Table of Artificial Sines and Tangents. Gunter wrote cotangens.

Cotangent is found in English in 1714 in The Young Gentleman’s Trigonometry: Containing Such Elements of Trigonometry, as are most Useful and Easy to be known by Edward Wells. [Google print search, James A. Landau]

COTANGENT SPACE is found in Louis Auslander, “The use of forms in variational calculations,” Pacific J. Math. Volume 5, Suppl. 2 (1955), 853-859.

The term COUNTABLE was introduced by Georg Cantor (1845-1918) (Kline, page 995). According to the University of St. Andrews website, he introduced the word in a paper of 1883.

In 1906 Theory of Sets of Points by W. H. Young and G. C. Young iv. 35 has “Any set which can be brought into (1, 1)-correspondence with some or all of the natural numbers is said to be countable, and, if not a finite set, is said to be countably infinite.” [OED]

COUNTING NUMBER is dated ca. 1965 in MWCD10.

COVARIANCE, ANALYSIS OF COVARIANCE. The term covariance, analogous to variance, began appearing in 1930 in the writings of R. A. Fisher and his circle. It is used in Fisher’s The Genetical Theory of Natural Selection (p. 195), Harold Hotelling’s "The Consistency and Ultimate Distribution of Optimum Statistics," Transactions of the American Mathematical Society, 32, p. 850 and H. G. Sanders’s "A Note on the Value of Uniformity Trials for Subsequent Experiments, Journal of Agricultural Science, 21, p. 64. In 1918 when Fisher introduced the term variance (q.v.) he announced the fact. In 1930 nobody said he was introducing a new term.

The term analysis of covariance has been used since 1932-and the 4^th edition of Fisher’s Statistical Methods for Research Workers--for a particular extension of the analysis of variance. The method--without the name--was the subject of Sanders’s "Note" of 1930; Sanders expressed his "great indebtedness" to Fisher. However, the name was used for a different extension of the analysis of variance by A. L. Bailey in a 1931 article, "The Analysis of Covariance," Journal of the American Statistical Association, 26, 424-435.

[John Aldrich, based on David (2001).]

The term COVARIANT was coined by James Joseph Sylvester. He used the term in 1851 in “On the general theory of associated algebraical forms,” Cambridge and Dublin Mathematical Journal. According to a reader of this web page, he introduced the term here.

Cayley at first used the term hyperdeterminant in this sense.

The term COVARIANT DIFFERENTIATION was introduced by Ricci and Levi-Civita (Kline, page 1127). According to a reader of this page, it was introduced in the paper “Sulla derivazione covariante ad una forma quadratica differenziale,” Rend. Acc. Lincei, 1887.

COVARIATE. When R. A. Fisher introduced the analysis of covariance he called the regression variable the concomitant variable. In the 1940s the term covariate came into use for the variable in that role: see e.g. Biometrics, 5, (1949), p. 73. (JSTOR search) More recently covariate has been detached from the analysis of covariance (and from the analysis of experiments) to be used more broadly. It is now employed where independent variable or exogenous variable or regressor might also be used. An early instance of this usage is found in D. A. Sprott and John D. Kalbfleisch "Examples of Likelihoods and Comparison with Point Estimates and Large Sample Approximations," Journal of the American Statistical Association, 64, (1969), p. 477. (JSTOR search)

See the entries COVARIANCE, DEPENDENT/INDEPENDENT VARIABLE, ENDOGENOUS/EXOGENOUS VARIABLE, REGRESSION.

The term COVECTOR was used in 1954 by two authors in two articles in Nieuw Archief voor Wiskunde. They are D. van Dantzig, “On the geometrical representation of elementary physical objects and the relations between geometry and physics” and D. Struik, “On free and attached vectors in affine and metric space.” Both articles are dedicated to J. A. Schouten.

COVERING (Belegung, from the verb Belegen = cover) was used by Georg Cantor in his last works (1895-97) on set theory, as shown in the following passage from Philip Jourdain’s translation (Contributions to the founding of the theory of transfinite numbers, Dover, 1915, p. 94):

By a "covering of the aggregate N with elements of the aggregate M," or, more simply, by a "covering of N with M," we understand a law by which with every element n of N a definite element of M is bound up, where one and the same element of M can come repeatedly into application. The element of M bound up with n is (...) called a "covering function of n". The corresponding covering of N will be called f (N).

The introduction of the concept of "covering" is the most striking advance in the principles of the theory of transfinite numbers from 1885 to 1895, (...)

COXETER GROUP. The term comes from the name Donald Coxeter (1907-2003). A survey book by James E. Humphreys, Reflection Groups and Coxeter Groups (1990), includes in its references a set of lecture notes written by Jacques T i t s in 1961 and called Groupes et Géométries de Coxeter. William C. Waterhouse provided this citation and believes the term was introduced by T i t s.

The terms groupes de Coxeter, matrice de Coxeter, graphe de Coxeter, and nombre de Coxeter are found in 1968 in N. Bourbaki, Groupes et algèbres de Lie [Heinz Lueneburg].

CRAMÉR-RAO INEQUALITY in the theory of statistical estimation. The inequality was obtained independently by at least three authors in the 1940s. The name "Cramér-Rao inequality" appears in Neyman & Scott (Econometrica, 1948) and recognises the English language publications of H. Cramér (1946 Mathematical Methods of Statistics) and C. R. Rao (1945 Bull. Calcutta Math. Soc. 37, 81-91). L. J. Savage (Foundations of Statistics 1954) drew attention to the work of M. Fréchet (1943) and G. Darmois (1945) and "tentatively proposed" the impersonal term "information inequality." However the name "Cramér-Rao inequality" has remained popular, though the "Fréchet-Darmois-Cramér-Rao inequality" figures in some French literature. [This entry contributed by John Aldrich, with some information from David (1995).]

CRAMÉR-VON MISES TEST. The test was proposed by Harald Cramér “On the composition of elementary errors,” Skandinavisk Aktuarietidskrift, 11, (1928), 13-74; 141-180 and independently by Richard von Mises Vorlesungen aus dem Gebiete der angewandten Mathematik. Bd I Wahrscheinlichkeitsrechnung und ihre Anwendung in der Statistik und theoretischen Physik (1931). For later literature see Encyclopedia of Mathematics.

CRAMER’S RULE for solving a set of linear equations was given in the Introduction à l'analyse des lignes courbes algébraique (1750) by Gabriel Cramer. T. Muir The Theory of Determinants in the Historical Order of Development vol. 1 p. 15 quotes a passage from p. 291 of Bézout "Recherches sur le degré des Équations résultantes de l'évanouissement des inconnues, & sur les moyens qu'il convient d'employer pour trouver ces Équations". Histoire de l'Académie royale des sciences Ann. 1764. It begins "M. Cramer a donné une règle générale pour.."

Katz writes that the method was also described by Colin Maclaurin in the posthumous Treatise of Algebra (1748). See DETERMINANT.

The term CRITERIA OF ESTIMATION was used by Sir Ronald Aylmer Fisher in his paper "On the Mathematical Foundations of Theoretical Statistics", Philosophical Transactions of the Royal Society, April 19, 1922. The criteria were of consistency, efficiency and sufficiency.

See also ESTIMATION, CONSISTENCY, EFFICIENCY and SUFFICIENCY.

CRITERION OF INTEGRABILITY is found in 1816 in Edin. Rev. XXVII: "The theorem, which is called the Criterion of Integrability" [OED].

The term CRITERION OF SUFFICIENCY. See SUFFICIENCY.

CRITICAL POINT is found in 1871 in A General Geometry and Calculus by Edward Olney [University of Michigan Historic Math Collection].

The terms CRITICAL REGION and BEST CRITICAL REGION were introduced in J. Neyman and E. S. Pearson’s "On the Problem of the Most Efficient Tests of Statistical Hypotheses," Philosophical Transactions of the Royal Society of London. Series A, 231. (1933), pp. 289-337.

Unbiased critical region appears in J. Neyman and E. S. Pearson’s "Contributions to the Theory of Testing Statistical Hypotheses," Statistical Research Memoirs, 1, 1-37. (David 2001.)

See also HYPOTHESIS AND HYPOTHESIS TESTING.

Since around 1940 CRITICAL VALUE has been used in Statistics in a set way, illustrated by, "denote by t₀ the critical value of t corresponding to a chosen significance level." This is from A Wald’s "The Fitting of Straight Lines if Both Variables are Subject to Error," Annals of Mathematical Statistics, 11, (1940), p. 291. "Critical value" was a natural development from the established term "critical region."

See CRITICAL REGION.

CROSS PRODUCT is found on p. 61 of Vector Analysis, founded upon the lectures of J. Willard Gibbs, second edition, by Edwin Bidwell Wilson (1879-1964), published by Charles Scribner’s Sons in 1909:

The skew product is denoted by a cross as the direct product was by a dot. It is written

C = A X B

and read A cross b. For this reason it is often called the cross product.

CROSS-RATIO. According to Taylor (p. 257), cross-ratio first appeared in Elements of Dynamic, Part 1, Kinematic (1878), p. 42, by William Kingdon Clifford (1845-1879). Clifford wrote "The ratio ab.cd : ac.bd is called a cross-ratio of the four points abcd ..."

See also ANHARMONIC RATIO, DOPPELVERHÄLTNISS.

CROSS-VALIDATION. M. Stone reviews earlier contributions in his “Cross-Validatory Choice and Assessment of Statistical Predictions,” Journal of the Royal Statistical Society, B, 36, (1974), pp. 111-147. His earliest reference to a publication in which the term “cross-validation” is used is a 1951 Symposium “The Need and Means of Cross-validation,” Educ. & Psychol. Measurement, 11.

CUBE. At the start of Book XI of the Elements Euclid defines a χύβος as “a solid figure contained by six equal squares.” See p. 425 of Fitzpatrick’s Greek-English Euclid. Heron used “hexahedron” for this purpose and used “cube” for any right parallelepiped (Smith vol. 2, page 292). According to the OED, the cube was originally a die for playing with.

The word went into Latin as cubus and then into French as cube. For English the OED quotes from Trevisa’s 14^th century translation of De Proprietatibus Rerum: “Suche a fygure is callyd Cubus” and Billingsley’s translation of Euclid (1571): “A Cube is a solide or bodely figure contayned vnder sixe equall squares.”

The word “hexahedron” exists in English but is rare. The OED has a quotation from A geometrical practise named Pantometria by Leonard Digges (1571): “Hexaedron or Cvbvs is a solide figure, enclosed with sixe equall squares.”

Cuboid was introduced by R. B. Hayward in his Elementary Solid Geometry (1891): “The need of some short word in the place of the polysyllabic ‘rectangular parallelepiped’ has been long felt. I have coined the word ‘cuboid’.” See the Wikipedia entries cube and cuboid.

See the entry POLYHEDRON.

CUBE ROOT is found in English in 1648 in Logarithmotechnia, or The construction and use of the logarithmeticall tables. By the helpe whereof, multiplication is performed by addition, division by subtraction, the extraction of the square root by bipartition, and of the cube root by tripartition, &c. Finally, the golden rule, and the resolution of triangles as well right lined as sphericall by addition and substraction. First published in the French tongue by Edmund Wingate, an English gentleman: and after translated into English by the same author. [James A. Landau]

The word CUBOCTAHEDRON was coined by Kepler, according to John Conway.

CUMULANT was used by James Joseph Sylvester in Phil. Trans. (1853) 1. 543: "The denominator of the simple algebraical fraction which expresses the value of an improper continued fraction" [OED].

In statistics, CUMULANT is a contraction of cumulative moment function, the term R. A. Fisher used when he first discussed these quantities in his "Moments and Product Moments of Sampling Distributions," Proceedings of the London Mathematical Society, Series 2, 30, (1929), 199-238. The explanation of the name is that the cumulative moment function of a particular order is a function of moments of the same and lower orders. Much of Fisher’s work had  been anticipated by Thiele in 1889 and -99. See the entry on SEMI-INVARIANT.

The term cumulant appeared in 1931 in R. A. Fisher and J. Wishart, "The Derivation of the Pattern Formulae of Two-Way Partitions From Those of Simpler Patterns," Proceedings of the London Mathematical Society, Ser. 2, 33, p.195. Harold Hotelling (J. Amer. Stat Assoc., 28, 1933, 374) reports that the abbreviation was his idea. (David 2001).

In Fisher’s 1929 paper the logarithm of the moment generating function, the "K function," generates cumulants. In 1931 Fisher called this function the "cumulative function." In 1937 he used the logarithm of the characteristic function and called it the cumulative function: see E. A. Cornish and Fisher, Moments and Cumulants in the Specification of Distributions. Revue de l'Institut International de Statistique, 5, 307-320. The name cumulant generating function appears in J. B. S. Haldane "The First Six Moments of χ² for an n-Fold Table with n Degrees of Freedom when some Expectations are Small," Biometrika, 29, (1938), 389-391.

Hald (1998, chapter 17) describes how cumulant generating functions, like characteristic functions, had been used since the time of Laplace. [John Aldrich].

See CHARACTERISTIC FUNCTION (1), MOMENT and PROBABILITY GENERATING FUNCTION.

CURL. Although this term was coined by Maxwell, it is believed that the concept first occurs in an 1839 paper by James MacCullagh entitled “An essay towards a dynamical theory of crystalline reflexion and refraction” read to the Royal Irish Academy on December 9, 1839, and published in Transactions of the Royal Irish Academy, vol 21. The author introduces a potential function, the norm of the curl of the displacement field, to develop a theory for the transmission of light in homogeneous and non-homogeneous media that is compatible with known properties of light, in the process correcting one of the deficiencies in Fresnel’s theory. His chief reason for this particular potential function is that it forces the waves to be transverse. The full paper can be found in the Collected Works of J. MacC, particularly pages 149-152, where the effect on the curl components of an orthogonal transformation is considered. This makes it clear that, although no compact notation for vectors had yet been developed, the modern concept of a vector as a (covariant) tensor, was well understood in the 1830s, and indeed much earlier. [This paragraph was contributed by Peter McCullagh.]

James Clerk Maxwell wrote the following letter to Peter Guthrie Tait on Nov. 7, 1870:

Dear Tait,

What do you call this? Atled?

I want to get a name or names for the result of it on scalar or vector functions of the vector of a point.

Here are some rough-hewn names. Will you like a good Divinity shape their ends properly so as to make them stick?

(1) The result of applied to a scalar function might be called the slope of the function. Lamé would call it the differential parameter, but the thing itself is a vector, now slope is a vector word, wheras parameter has, to say the least, a scalar sound.

(2) If the original function is a vector then applied to it may give two parts. The scalar part I would call the Convergence of the vector function, and the vector part I would call the Twist of the vector function. Here the word twist has nothing to do with a screw or helix. If the word turn or version would do they would be better than twist, for twist suggests a screw. Twirl is free from the screw notion and is sufficiently racy. Perhaps it is too dynamical for pure mathematicians, so for Cayley’s sake I might say Curl (after the fashion of Scroll). Hence the effect of on a scalar function is to give the slope of that scalar, and its effect on a vector function is to give the convergence and the twirl of that function. The result of ² applied to any function may be called the concentration of that function because it indicates the mode in which the value of the function at a point exceeds (in the Hamiltonian sense) the average value of the function in a little spherical surface drawn round it.

Now if be a vector function of and F a scalar function of ,
F is the slope of F
V.F is the twirl of the slope which is necessarily zero
S.F = ²F is the convergence of the slope, which is the concentration of F.
Also S is the convergence of
V is the twirl of .

Now, the convergence being a scalar if we operate on it with , we find that it has a slope but no twirl.

The twirl of is a vector function which has no convergence but only a twirl.

Hence, ², the concentration of , is the slope of the convergence of together with the twirl of the twirl of , the sum of two vectors.

What I want to ascertain from you if there are any better names for these things, or if these names are inconsistent with anything in Quaternions, for I am unlearned in quaternion idioms and may make solecisms. I want phrases of this kind to make statements in electromagentism and I do not wish to expose either myself to the contempt of the initiated, or Quaternions to the scorn of the profane.

 × V = curl V."

See VECTOR ANALYSIS.

CURRIED FUNCTION. According to The Free On-line Dictionary of Computing:

It was named after the logician Haskell Curry but the 19th-century formalist Frege was the first to propose it and it was first referred to in ["Uber die Bausteine der mathematischen Logik", M. Schoenfinkel, Mathematische Annalen. Vol 92 (1924)]. David Turner said he got the term from Christopher Strachey who invented the term "currying" and used it in his lecture notes on programming languages written circa 1967.

CURVATURE. Nicole Oresme assumed the existence of a measure of twist called curvitas. Oresme wrote that the curvature of a circle is "uniformus" and that the curvature of a circle is proportional to the multiplicative inverse of its radius.

A translation of Isaac Newton in Problem 5 of his Methods of series and fluxions is:

A circle has a constant curvature which is inversely proportional to its radius. The largest circle that is tangent to a curve (on its concave side) at a point has the same curvature as the curve at that point. The center of this circle is the "centre of curvature" of the curve at that point.

Curvature is found in English in 1698 in Philosophical Transactions: Giving Some Account of the Present Undertakings, Studies and Labours of the Ingenious in Many Considerable Parts of the World Vol. XIX. For the Years 1695, 1696, and 1697: London: 1698 “. . .shews how it comes that spherical Surfaces produce the same effects with those of certain Spheroids and Conoids, viz. because they have the same degree of Curvature.” [Google print search, James A. Landau]

Curvature appears in English in 1710 in Lexicon technicum, or an universal English dictionary of arts and sciences by John Harris, in which it is stated that "the Curvatures of different Circles are to one another Reciprocally as their Radii" (OED1).

CURVE FITTING appears in a paper read in June 1901 by Karl Pearson, "On the Mathematical Theory of Errors of Judgment, with Special Reference to the Personal Equation", Philosophical Transactions of the Royal Society of London. Series A, 198, (1902), 235-299. A footnote therein (p. 289) mentions a memoir on the "general theory of curve fitting" to appear in Biometrika. This was Pearson’s "On the Systematic Fitting of Curves to Observations and Measurements," Biometrika, 1, (1902), pp. 265-303. [James A. Landau]

CURVE OF PURSUIT. The name ligne de poursuite "seems due to Pierre Bouguer (1732), although the curve had been noticed by Leonardo da Vinci" (Smith vol. 2, page 327).

The term CW-COMPLEX was introduced by J.H.C. Whitehead, “Combinatorial homotopy I” Bulletin of the American Mathematical Society, 55, (1949), 213–245. “By a CW-complex we mean one which is closure finite and has the weak topology.” (p. 223). Thus CW comes from the first letters of the names for the two conditions, closure finiteness and weak topology. See the Encyclopedia of Mathematics entry.

The term CYBERNETICS was coined by Norbert Wiener. In his book Cybernetics (1948, p.19) Wiener explained, "We have decided to call the entire field of control and communication theory, whether in the machine or in the animal, by the name Cybernetics, which we form from the Greek , or steersman. In choosing this term, we wish to recognize that the first significant paper on feedback mechanisms is an article on governors, which was published by Clerk Maxwell in 1866, and that governor is derived from a Latin corruption of ." Wiener’s father was a philology professor.

CYCLE (in a modern sense) was coined by Edmond Nicolas Laguerre (1834-1886).

CYCLIC GROUP. The term cyclical group was used by Cayley in "On the substitution groups for two, three, four, five, six, seven, and eight letters," Quart. Math. J. 25 (1891).

The term also appears in 1898 in Introduction to the theory of analytic functions by J. Harkness and F. Morley: "Such a group is called a cyclic group and S is called the generating substitution of the group."

CYCLIC PERMUTATION. Permutation circulaire is found in Cauchy’s 1815 memoir "Sur le nombre des valeurs q'une fonction peut acquérir lorsqu'on permute de toutes les manières possibles les quantités qu'elle renferme" (Journal de l'Ecole Polytechnique, Cahier XVII = Cauchy’s Oeuvres, Second series, Vol. 13, pp. 64--96.) This usage was found by Roger Cooke, who believes this is the first use of the term.

CYCLIC QUADRILATERAL. Inscriptible polygon is found in about 1696 in Scarburgh, Euclid (1705): "Polygons do arise, that are mutually with a Circle, or with one another Inscriptible and Circumscriptible" [OED].

Inscribable is found in the 1846 Worcester dictionary.

Inscriptible quadrilateral is found in 1857 in Mathematical Dictionary and Cyclopedia of Mathematical Science.

Cyclic quadrilateral is found in 1888 in Casey, Plane Trigonometry [OED].

The CYCLOID was named by Galileo Galilei (1564-1642) (Encyclopaedia Britannica, article: "Geometry"). According to the website at the University of St. Andrews, he named it in 1599.

Cycloid is found in English in 1667 in The History of the Royal-Society of London, For the Improving of Natural Knowledge by Tho. Sprat: “A Discourse of making the several Vibrations of a Pendulum aequal, by making the weight of it move in Cycloid instead of a Circle.” [Google print search, James A. Landau]

The word cycloid appears in Moby Dick by Herman Melville: "It was in the left hand try-pot of the Pequod, with the soapstone diligently circling round me, that I was first indirectly struck by the remarkable fact, that in geometry all bodies gliding along the cycloid, my soapstone for example, will descend from any point in precisely the same time."

CYCLOTOMY and CYCLOTOMIC were used by James Joseph Sylvester in his “On Certain Ternary Cubic-Form Equations,” American Journal of Mathematics, (4), (1879), p. 357 to translate the German word Kreisteilung (circle-division). (OED).

CYLINDER is defined in Euclid XI. The Greek word 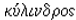went into Latin as cylindrus and thence into French and English.

The earliest citation in the OED is from 1570: Billingsley’s translation of the definition of Euclid, “A cylinder is a solide or bodely figure which is made, when one of the sides of a rectangle parallelogramme, abiding fixed, the parallelogramme is moued about.”